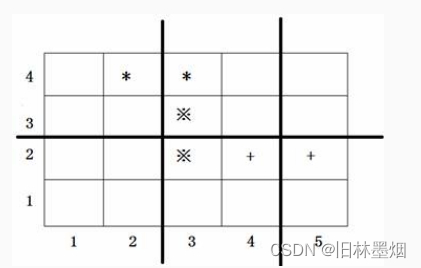
（1）题目分析如下 

题目要求完成一个正则表达式的匹配，其中s为目标串，p为正则串

.符号代表任何字符，*符号代表把前一个字符重复n次（可能为0次）

（2）具体思路

一开始的时候想过贪心算法，但是贪心算法无法匹配这种aaa--a*a，所以这题我们只能采用动态规划的模式：（或者递归）

建立二维数组int arr[i][j]，代表s字符串的前i个和p字符串的前j个能否进行匹配

1.如果p[j]

目前指向的不是*符号，那么就代表当前是一一字符进行比较的，如果是s[i]==p[j]，那么就arr[i][j]的值就由上一个情况决定，即arr[i][j]=arr[i-1][j-1]........

如果ij对应的字符不是匹配的，那么就认为arr[i][j]=0

2.如果p[i]='*'

如果s[i]==p[i-1],相当于s[i]末尾可能是多个复制的结果，所以可能为arr[i][j]=arr[i-1][j];

但是这这种情况，比如aab和aaa*b，这种情况下【2】和【4-1】确实能匹配上，但是【2】【2】已经完成了匹配，这种情况下其实就是虽然能对上，但本质上还是复制了零次，所以也可能为arr[i][j]=arr[i][j-2]

但是如果不相等就没辙了，真的就代表复制了0次，arr[i][j]=arr[i][j-2]

上述过程抽象一下应该就是回归方程了

另外，二维数组从1开始，说明我们要对二维数组两个0有关的列，当时 j为0（对应p串为空），arr[i][j]=0;

当i=0（s串为空），此时p串如果j为星号，可能是复制了0次，arr[0][j]=arr[0][j-2] ，如果j不是*，那就妥妥的匹配不上，arr[i][j]=0;

最后补充初始情况，arr【0】【0】=1；

具体代码实现如下

（注意这里把字符串延长匹配了一下）

bool isMatch(string s, string p) {
    s=" "+s;
    p=" "+p;
    //上面是为了配合动态规划，认为加长一下，动态规划一般不都是默认从1开始，然后边界情况单独初始化吗
    //这道题中的边界情况就是
    int arr[31][31];
    for(int i=0;i<=s.length()-1;i++)
        for(int j=0;j<=p.length()-1;j++)
            if(i==0||j==0)
                arr[i][j]=0;
    arr [0][0]=1;
    for(int j=1;j<=p.length()-1;j++) {
        if (p[j] == '*') {
            arr[0][j] = arr[0][j - 2];
        } else {
            arr[0][j] = 0;
        }
    }
    //初始化数组完成
    for(int i=1;i<=s.length()-1;i++){
        for(int j=1;j<=p.length()-1;j++){
            if(p[j]!='*'){
                if(s[i]==p[j]||p[j]=='.'){
                    arr[i][j]=arr[i-1][j-1];
                }else{
                    arr[i][j]=0;
                }
            }else{
                if(s[i]==p[j-1]||p[j-1]=='.'){
                    arr[i][j]=(arr[i-1][j] || arr[i][j-2]);
                }else{
                    arr[i][j]=arr[i][j-2];
                }
            }
        }
    }
    for(int i=0;i<=s.length()-1;i++) {
        for (int j = 0; j <= p.length() - 1; j++) {
            cout<<arr[j][i];
        }
        cout<<endl;
    }
    return arr[s.length()-1][p.length()-1];
}