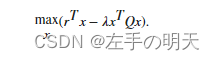输入矢量x是原始的输入数据，而q、k、v是通过对x进行线性变换得到的新的表示。q、k、v是通过对x分别乘以三个矩阵Wq、Wk、Wv得到的，其中Wq、Wk、Wv是通过学习得到的参数矩阵。这些参数矩阵通过模型训练过程中的反向传播算法来更新，以使得模型能够更好地进行特征提取和表示学习。

q矩阵是用来计算注意力权重，用于表示输入数据的重要性；k矩阵是用来计算注意力权重，用于表示输入数据之间的相关性；v矩阵是用来计算注意力权重，用于表示输入数据的表示向量。

通过对输入数据进行线性变换，可以将原始的输入数据映射到一个更高维的表示空间，以便模型更好地理解和处理输入数据。通过学习参数矩阵Wq、Wk、Wv，模型可以根据输入数据的特点和任务的需求，自动调整这些矩阵的值来提取更有意义和有用的表示信息。

假设我们有一个输入矢量x，我们通过线性变换来得到q，k，v三个矢量。具体来说，我们可以使用权重矩阵Wq，Wk，Wv来对输入矢量进行线性变换。

假设输入矢量x是一个n维向量，我们使用一个n×m的权重矩阵Wq来对其进行变换，得到一个m维向量q。同样地，我们使用一个n×m的权重矩阵Wk和一个n×m的权重矩阵Wv来分别对输入矢量进行变换，得到m维的k和v。

因此，输入矢量x和变换后的q，k，v的区别在于维度的改变。输入矢量x是一个n维向量，而q，k，v是m维向量（其中m可能与n不相等）。Wq，Wk，Wv的确定通常是通过训练模型来获得。在训练过程中，模型会尝试学习合适的权重值，使得变换后的q，k，v能够更好地用于后续的操作，比如注意力计算。常见的方式是使用梯度下降等优化算法来最小化损失函数，优化权重矩阵的取值。

在结合态势感知场景中，我们希望通过输入矢量x来生成q，k，v这三个矢量，以便进行后续的注意力机制操作。首先，x是输入矢量，可以是任意形式的数据，例如图像、文本、声音等。对于不同的任务和应用，输入的矢量x具有不同的含义和表示方式。

q，k，v是经过线性变换得到的矢量。它们分别代表了查询（query）、键（key）和值（value）。在注意力机制中，q和k用于计算注意力权重，而v则根据注意力权重计算加权和。简单来说，q，k，v起到了对输入矢量x进行映射并提取其关键信息的作用。

Wq，Wk，Wv是线性变换的权重矩阵，用于将输入矢量x变换为q，k，v三个矢量。这些权重矩阵通过学习得到，通常通过训练神经网络来学习参数。具体地，线性变换可以看作是将输入矢量x投影到一个不同的向量空间中，从而得到q，k，v。

概况而言，q，k，v是通过对输入矢量x进行线性变换得到的，它们分别表示查询、键和值的信息。Wq，Wk，Wv是线性变换的权重矩阵，用于确定如何对输入矢量x进行变换。

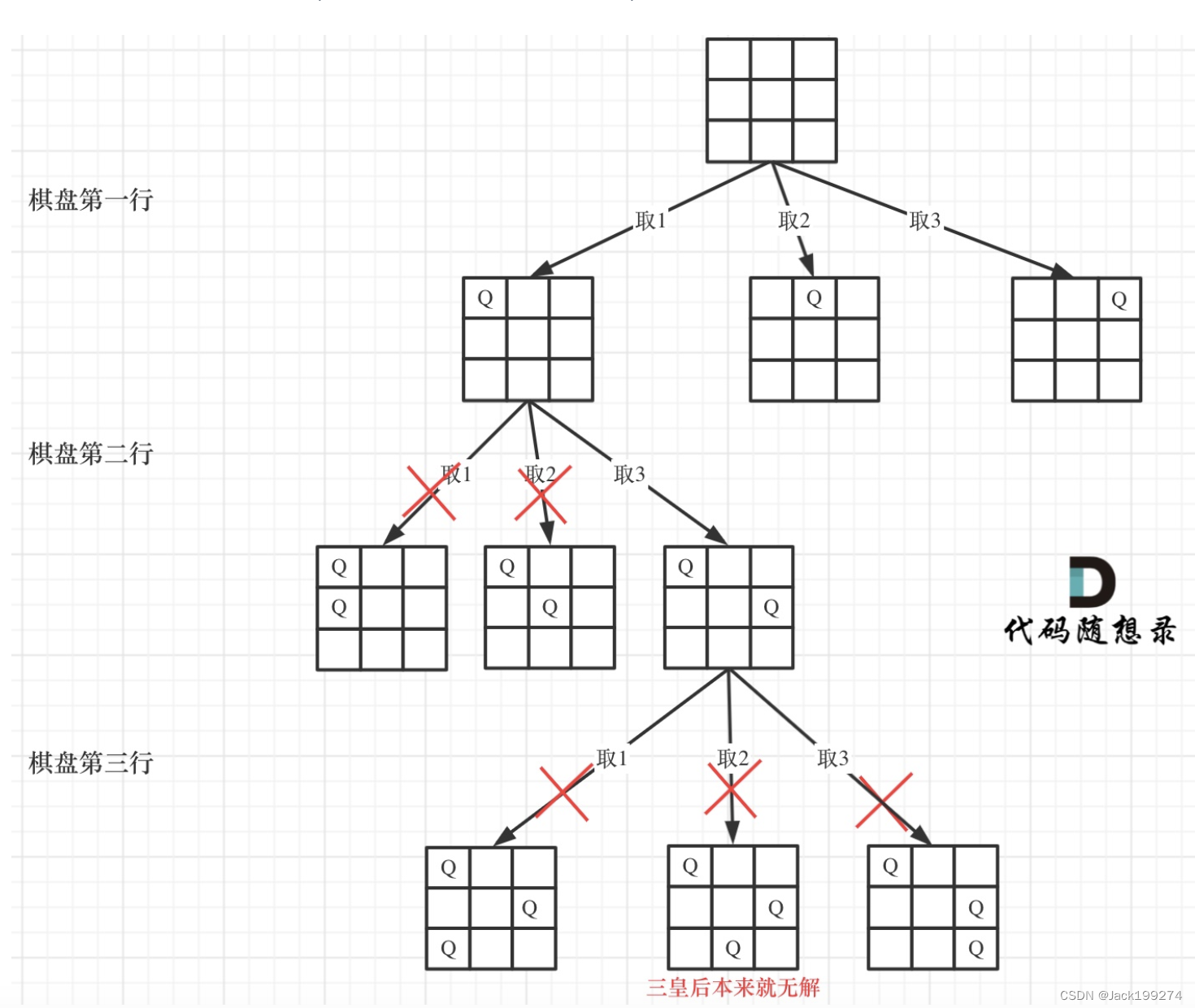
在博弈态势感知中，查询向量、键向量和数值向量是用来描述和表示不同方面的信息的。举例说明：假设有一个棋局的博弈态势感知系统，它需要从当前棋局中提取关键信息，以便于决策最佳的下一步棋。

查询向量（Query Vector）：查询向量是用来表示博弈系统当前关注的特定方面的信息，通常由一组特征表示。例如，查询向量可以包括当前棋局中的棋子在不同位置的分布情况、当前玩家的回合数等信息。查询向量可以帮助系统关注特定的问题或特定的状态。

键向量（Key Vector）：键向量是博弈系统中存储信息的索引，它用于检索和访问特定的数值向量。例如，在棋局中，键向量可以用来表示每个棋子的位置和状态。键向量通常是由唯一的标识符或特征向量表示的。

数值向量（Value Vector）：数值向量是与键向量相关联的具体数值或状态信息。例如，在棋局中，数值向量可以表示每个棋子的类型、颜色和可行的移动方式等。数值向量可以提供与特定键向量相关的具体信息。

总结起来，查询向量用于关注特定的问题或状态，键向量用于索引和检索信息，而数值向量提供与键向量相关的具体信息。这些向量可以协助博弈系统感知当前的棋局态势，并作出相应的决策。