332.重新安排行程
题目链接:重新安排行程
解法:
这个题,卡哥的思路会超时。辛辛苦苦看懂了卡哥的思路,结果超时了,直接崩溃。
看了leetcode官方的思路,非常简洁,但是里面的深意还是不太懂。
- 由于题目中说必然存在一条有效路径(至少是半欧拉图),所以算法不需要回溯(既加入到结果集里的元素不需要删除)
- 整个图最多存在一个死胡同(出度和入度相差1),且这个死胡同一定是最后一个访问到的,否则无法完成一笔画。
- DFS的调用其实是一个拆边的过程(既每次递归调用删除一条边,所有子递归都返回后,再将当前节点加入结果集保证了结果集的逆序输出),一定是递归到这个死胡同(没有子递归可以调用)后递归函数开始返回。所以死胡同是第一个加入结果集的元素。
- 最后逆序的输出即可。
边界条件:
时间复杂度:O(mlogm),其中 m 是边的数量。对于每一条边我们需要 O(logm) 地删除它,最终的答案序列长度为 m+1,而与 n 无关。
空间复杂度:O(m),其中 m 是边的数量。我们需要存储每一条边。
class Solution:
def findItinerary(self, tickets):
import heapq
from collections import defaultdict
self.ticket_path = defaultdict(list)
for depart, arrival in tickets:
self.ticket_path[depart].append(arrival)
for key in self.ticket_path:
heapq.heapify(self.ticket_path[key])
self.result = []
self.traversal('JFK')
return self.result[::-1]
def traversal(self, depart):
while self.ticket_path[depart]:
arrival = heapq.heappop(self.ticket_path[depart])
self.traversal(arrival)
self.result.append(depart)51. N皇后
题目链接:https://leetcode.com/problems/n-queens/
解法:
可以将过程抽象为一棵树,
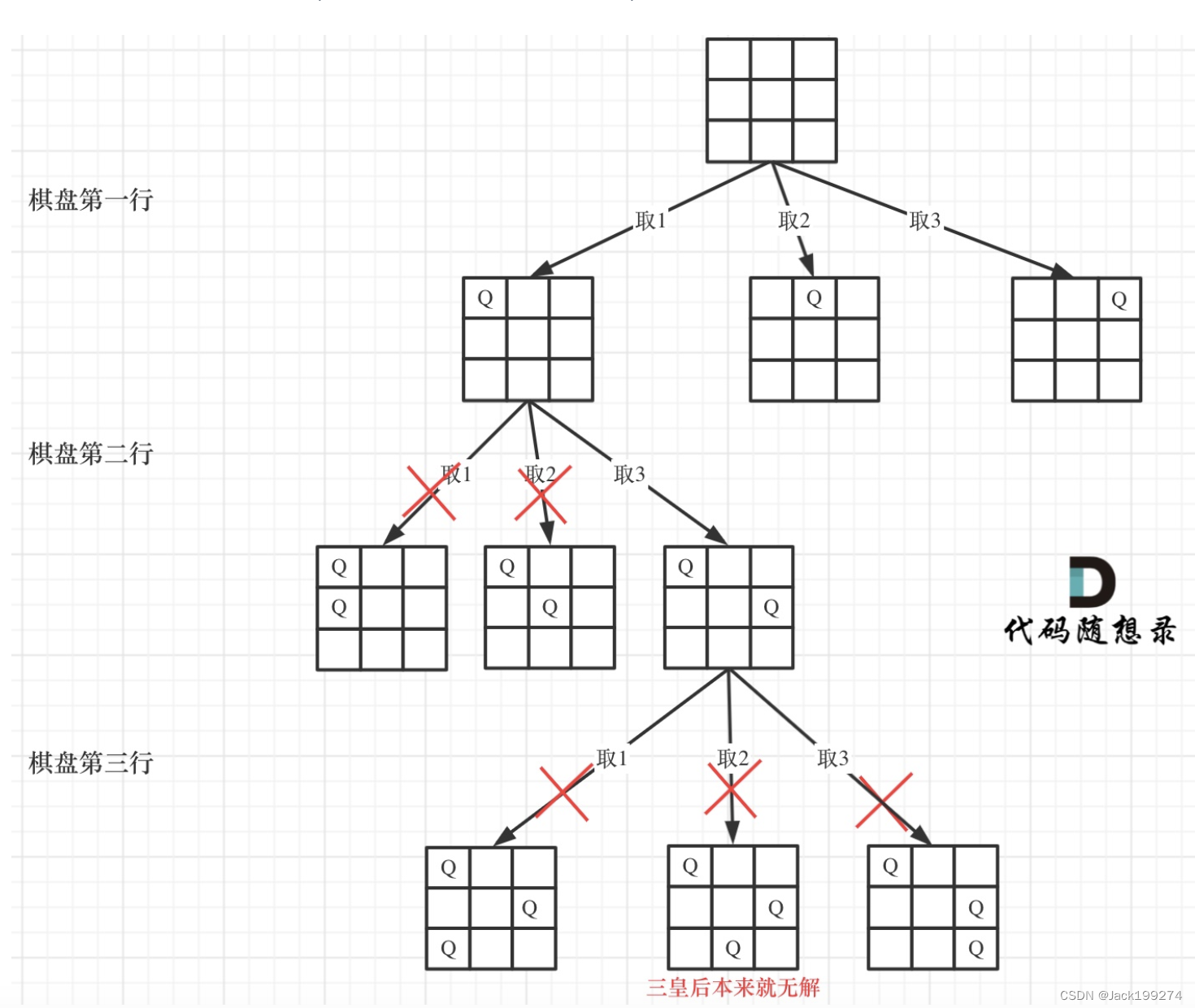
其他的细节,直接看题解好了:代码随想录-n皇后
边界条件:无
时间复杂度:O(n!)
空间复杂度:O(n)
class Solution(object):
def solveNQueens(self, n):
self.result = []
self.dashboard = ['.' * n for _ in range(n)]
self.traversal(n, 0)
return self.result
def traversal(self, n, row):
# 如果最后一行填满了,返回
if row == n:
self.result.append(self.dashboard[:])
return
for col in range(n):
if self.isValid(row, col):
self.dashboard[row] = self.dashboard[row][:col] + 'Q' + self.dashboard[row][col+1:]
self.traversal(n, row+1)
self.dashboard[row] = self.dashboard[row][:col] + '.' + self.dashboard[row][col+1:]
def isValid(self, row, col):
# 检查同一列是否已经存在皇后,
# 如果同一个col,上面的row已经存在,则不能再放
for i in range(row):
if self.dashboard[i][col] == 'Q':
return False
# 检查左上角是否已经存在皇后
i, j = row - 1, col - 1
while i >= 0 and j >= 0:
if self.dashboard[i][j] == 'Q':
return False
i -= 1
j -= 1
# 检查右上角是否已经存在皇后
i, j = row - 1, col + 1
while i >= 0 and j < len(self.dashboard):
if self.dashboard[i][j] == 'Q':
return False
i -= 1
j += 1
return True37. 解数独
题目链接:解数独
解法:
这道题真的挺复杂的,代码写出来以后,看似明白了,待自己模拟运行一遍,就会发现其实理解还有待加强。算法的复杂度那是相当的高。
直接看题解吧:代码随想录-解数独
边界条件:无
时间复杂度:
空间复杂度:
class Solution(object):
def solveSudoku(self, board):
"""
:type board: List[List[str]]
:rtype: None Do not return anything, modify board in-place instead.
"""
self.traversal(board)
def traversal(self, board):
for i in range(9):
for j in range(9):
if board[i][j] != '.': continue
for val in range(1, 10):
if self.isValid(i, j, board, str(val)):
board[i][j] = str(val)
if self.traversal(board):
return True
board[i][j] = '.'
return False
return True
def isValid(self, row, col, board, val):
# check the same row
for i in range(9):
if board[row][i] == val:
return False
# check the same column
for j in range(9):
if board[j][col] == val:
return False
# check subbox
startRow = (row // 3) * 3
startCol = (col // 3) * 3
for row in range(startRow, startRow+3):
for col in range(startCol, startCol+3):
if board[row][col] == val:
return False
return True