🔗 运行环境:Matlab、Python
🚩 撰写作者:左手の明天
🥇 精选专栏:《python》
🔥 推荐专栏:《算法研究》
#### 防伪水印——左手の明天 ####
💗 大家好🤗🤗🤗,我是左手の明天!好久不见💗
💗今天分享matlab数学建模算法——混合整数二次规划 (MIQP) 投资组合优化问题💗
📆 最近更新:2023 年 11 月 28 日,左手の明天的第 297 篇原创博客
📚 更新于专栏:matlab
#### 防伪水印——左手の明天 ####
一、混合整数二次规划投资组合优化问题
混合整数二次规划投资组合优化是一个复杂的问题,需要考虑多种因素,如投资者的风险承受能力、投资组合的预期收益、投资组合中不同资产的权重限制等等。
1.投资组合选择
在投资组合选择方面,通常我们需要根据个人的风险承受能力、投资期限、资产规模等因素来选择投资组合。在这个过程中,我们需要考虑不同资产之间的相关性、历史收益率、波动率等因素。通过混合整数二次规划方法,我们可以优化投资组合的权重分配,从而在满足风险承受能力限制的同时,最大化投资组合的预期收益。
2.资产配置
资产配置是指在不同资产之间进行权重的分配。通过混合整数二次规划方法,我们可以根据历史收益率、波动率等因素,对不同资产进行权重的分配,从而优化投资组合的表现。在资产配置过程中,我们还需要考虑不同资产之间的相关性以及市场风险等因素。
3.风险评估
风险评估是投资组合优化的重要环节之一。通过混合整数二次规划方法,我们可以根据历史数据和模型预测,对投资组合的风险进行评估和预测。在这个过程中,我们需要考虑不同资产之间的相关性、波动率等因素,以及市场风险和系统风险等因素。通过风险评估,我们可以更好地了解投资组合的风险状况,从而制定更加合理的投资策略。
4.投资策略优化
投资策略优化是指根据个人的风险承受能力、投资期限等因素,制定适合的投资策略。通过混合整数二次规划方法,我们可以根据历史数据和模型预测,对投资组合的表现进行优化。在这个过程中,我们需要考虑不同资产之间的相关性、波动率等因素,以及市场风险和系统风险等因素。通过投资策略优化,我们可以更好地掌握市场的变化,从而获得更加稳定的收益。
5.约束条件处理
在混合整数二次规划投资组合优化中,我们需要考虑一些约束条件,如投资组合的权重总和为1、每个资产的权重非负等。通过约束条件处理,我们可以确保投资组合的权重分配符合要求,同时优化投资组合的表现。在约束条件处理中,我们还需要考虑不同约束条件的优先级和重要性等因素。
6.算法设计
混合整数二次规划算法是一种常用的优化算法,它可以解决带有约束条件的二次规划问题。在算法设计方面,我们需要根据问题的特点来设计合适的算法。常见的混合整数二次规划算法包括分支定界法、割平面法等。通过算法设计,我们可以高效地求解优化问题,从而得到最优解。
7.实证分析
最后,我们可以通过实证分析来验证混合整数二次规划投资组合优化的有效性。在实证分析中,我们需要选择合适的样本数据和评估指标,然后对模型进行训练和测试。通过与基准组合和其他投资组合进行比较,我们可以评估混合整数二次规划投资组合优化的表现。此外,我们还可以对模型进行参数调整和敏感性分析等操作,以进一步优化模型的表现。
二、混合整数二次规划投资组合优化模型的具体目标
在满足风险承受能力限制的同时,最大化投资组合的预期收益。也就是说,我们希望找到一种投资组合,它可以使我们在预期的情况下获得最大的收益,同时不超过我们设定的风险水平。这是一个典型的权衡问题,即在风险和收益之间找到一个最佳的平衡点。
三、问题概要
可以将许多投资组合优化问题表达为二次规划问题。假设有包含 N 项的一组资产并希望选择一个投资组合,其中 x(i) 是在 i 资产中的投资比例。如果知道每项资产平均回报的向量 r,以及回报的协方差矩阵 Q,则对于给定的风险厌恶水平 λλ,需要最大化风险调整后的预期回报:
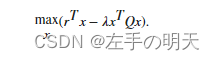
quadprog 求解器用于求解此二次规划问题。但是,除了简单的二次规划问题之外,还可能希望以多种方式限制投资组合,例如:
-
投资组合中资产不超过
M种,其中M <= N。 -
投资组合中至少有
m种资产,其中0 < m <= M。 -
具有半连续约束,意味着对某些固定比例 fmin>0 和 fmax≥fmin,x(i)=0 或 fmin≤x(i)≤fmax。
四、Matlab实现混合整数二次规划投资组合优化
要在MATLAB中实现混合整数二次规划投资组合优化,可以使用MATLAB的优化工具箱,例如quadprog函数。以下是一个基本的示例:
首先,假设你已经有了资产的历史收益率数据,将这些数据存储在矩阵
returns中,每一列代表一个资产,每一行代表一个时间点。你也需要一个矩阵rho来存储风险系数,和一个标量mu来存储预期收益率。然后,你可以定义你的变量,即投资组合的权重
w,并将它们存储在一个向量中。在这个例子中,我们假设有5个资产,所以w应该是一个5x1的向量。接着,你可以定义你的目标函数和约束条件。在这个例子中,我们的目标函数是最大化预期收益(
mu'*w)减去风险(rho*w'*w),我们有两个约束条件:投资组合的权重总和为1(sum(w) == 1),以及每个资产的权重非负(w >= 0)。
最后,可以使用quadprog函数来求解这个问题。这个函数需要一个Hessian矩阵(在这个例子中是2n的矩阵,其中n是资产数量),以及一个线性约束矩阵(在这个例子中是1n的矩阵)。
以下是一个基本的实现:
% 历史收益率数据
returns = [0.05, 0.1, 0.15, 0.2, 0.25];
n = length(returns); % 资产数量
T = length(returns); % 时间点数量
% 定义变量
w = Variable(n);
% 定义预期收益率和风险系数
mu = mean(returns); % 预期收益率
rho = 0.2; % 风险系数
% 定义目标函数和约束条件
objective = Maximize(mu' * w - 0.5 * rho * sum(w.^2));
constraints = [sum(w) == 1, w >= 0];
% 定义Hessian矩阵和线性约束矩阵
H = sparse([1:n 1:n], [1:n 1:n], [], n, n); % Hessian矩阵
A = sparse([1:n], [1:n], [], n, n); % 线性约束矩阵
b = ones(n, 1); % 线性约束边界条件
% 使用quadprog求解优化问题
options = optimoptions('quadprog', 'Algorithm', 'interior-point-convex');
[x,fval,exitflag,output] = quadprog(H, -A', b, [], [], [], [], constraints(1), constraints(2), [], options);
% 输出结果
disp('最优解:');
disp(x);请注意,这只是一个基本的示例,可能需要根据你的具体需求进行调整。例如,你可能需要考虑其他的约束条件,或者使用其他的优化算法。此外,你也需要确保你有正确的工具箱许可证来使用quadprog函数。
五、python实现混合整数二次规划投资组合优化
以下是一个简单的混合整数二次规划投资组合优化模型的例子:
假设有n个资产,每个资产的历史收益率数据已知。我们需要构建一个投资组合,使得在满足风险承受能力限制的同时,最大化投资组合的预期收益。
目标函数:最大化预期收益 约束条件:投资组合的权重总和为1,每个资产的权重非负;投资组合的风险小于等于给定的风险承受能力限制。
以下是一个混合整数二次规划投资组合优化的Python代码示例:
import numpy as np
from cvxpy import *
# 历史收益率数据
returns = np.array([0.05, 0.1, 0.15, 0.2, 0.25])
n = len(returns)
# 定义变量
w = Variable(n)
mu = np.mean(returns) # 预期收益
rho = 0.2 # 风险系数
# 定义目标函数和约束条件
objective = Maximize(mu * sum(w) - 0.5 * rho * sum(w**2))
constraints = [sum(w) == 1, w >= 0, w <= np.ones(n)]
# 定义优化问题
problem = Problem(objective, constraints)
# 使用CVXPY求解优化问题
result = problem.solve()
# 输出结果
print("最优解:", result)
print("最优投资组合:")
for i in range(n):
if result[i] > 0:
print(i+1, ":", result[i])在这个例子中,我们使用了CVXPY库来求解优化问题。我们首先定义了历史收益率数据,然后定义了变量和约束条件。我们的目标函数是最大化预期收益减去风险系数的平方和,约束条件包括投资组合的权重总和为1、每个资产的权重非负以及投资组合的风险小于等于给定的风险承受能力限制。最后,我们使用CVXPY求解优化问题并输出结果。