🌈欢迎来到数据结构专栏~~二叉树的非递归遍历

---

• (꒪ꇴ꒪(꒪ꇴ꒪ )🐣,我是Scort
• 目前状态：大三非科班啃C++中
• 🌍博客主页：张小姐的猫~江湖背景
• 快上车🚘，握好方向盘跟我有一起打天下嘞！
• 送给自己的一句鸡汤🤔：
• 🔥真正的大师永远怀着一颗学徒的心
• 作者水平很有限，如果发现错误，可在评论区指正，感谢🙏
• 🎉🎉欢迎持续关注！
  

1️⃣二叉树的前序遍历

题目链接：传送

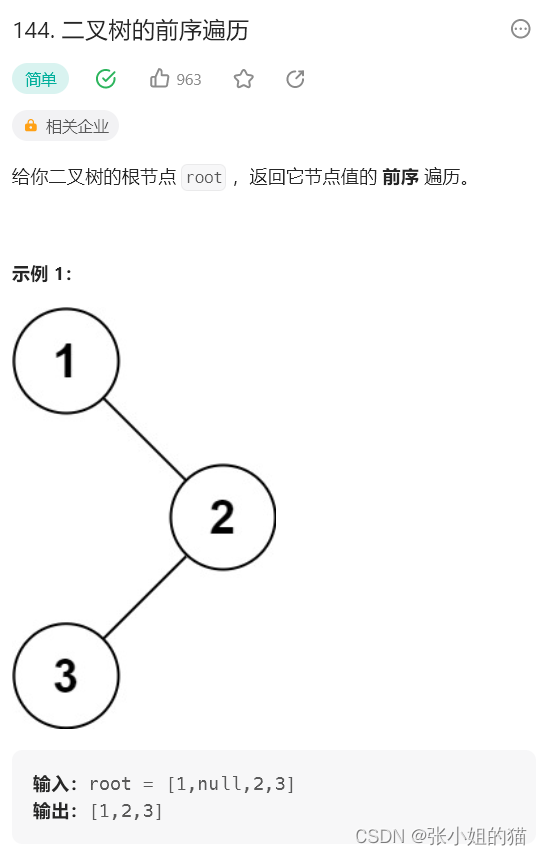
本文我们都采用非递归的方法去讲解：

本质上是在模拟递归，因为在递归的过程中使用了系统栈，所以在迭代的解法中常用Stack来模拟系统栈

思路：

1. 二叉树的左子树不断入栈，同时也入数组
2. 当左子树都访问完了，要访问右子树的时候，取出栈顶的top元素，并且子问题访问右子树：cur = top->right
3. 如此一来可以访问完全部的左右子树

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode* cur = root;

        while(cur || !st.empty())
        {
            //开始访问一颗树的左边节点
            while(cur)
            {
                v.push_back(cur->val);
                st.push(cur);

                cur = cur->left;
            }

            //左边节点的右路指针需要访问
            TreeNode* top = st.top();
            st.pop();

            cur = top->right;//子问题访问右树  重点！！
        }
        return v;
    }
};

2️⃣二叉树的中序遍历

题目链接：传送

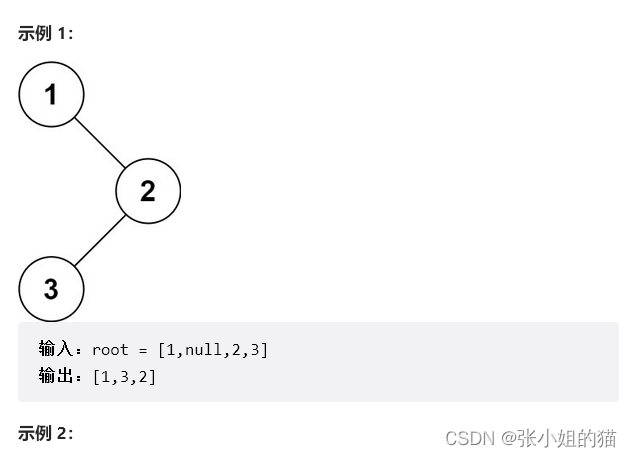
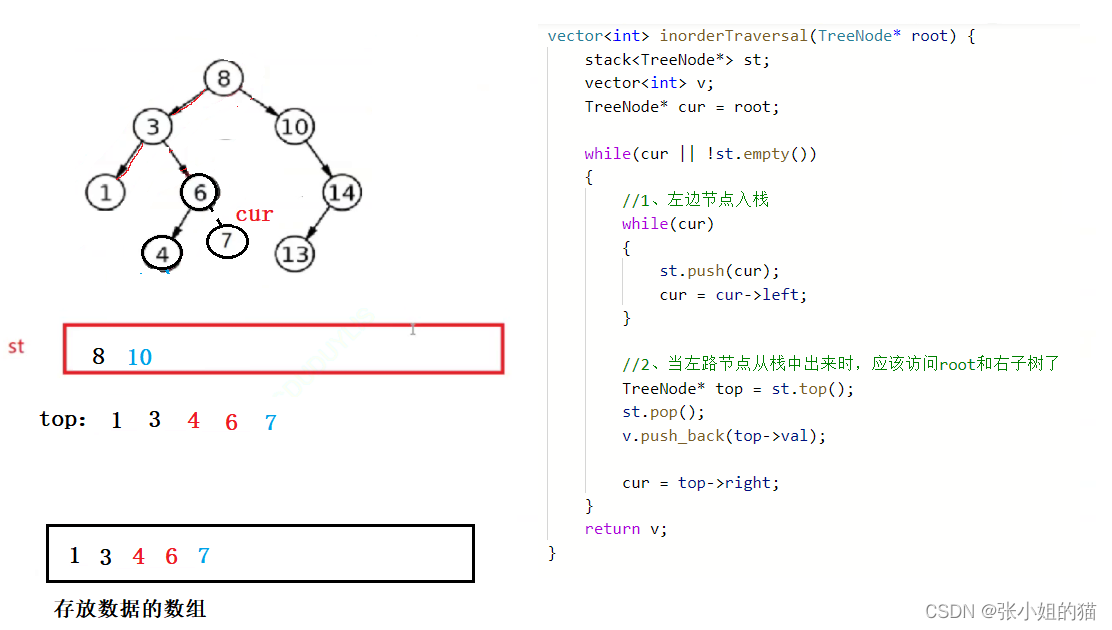
思路：

• 要记住中序：左子树 —— 根 —— 右子树
• 当cur 不为空或者栈不为空的时候，就说明还没有遍历完
• 左边节点全部入栈后，遇到空的时候，就要去栈顶top，并且cur = top->right，变到右子树继续

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode* cur = root;

        while(cur || !st.empty())
        {
            //1、左边节点入栈
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }

            //2、当左路节点从栈中出来时，应该访问root和右子树了
            TreeNode* top = st.top();
            st.pop();
            v.push_back(top->val);
            
            cur = top->right;
        }
        return v;
    }
};

3️⃣二叉树的后序遍历

题目链接：传送

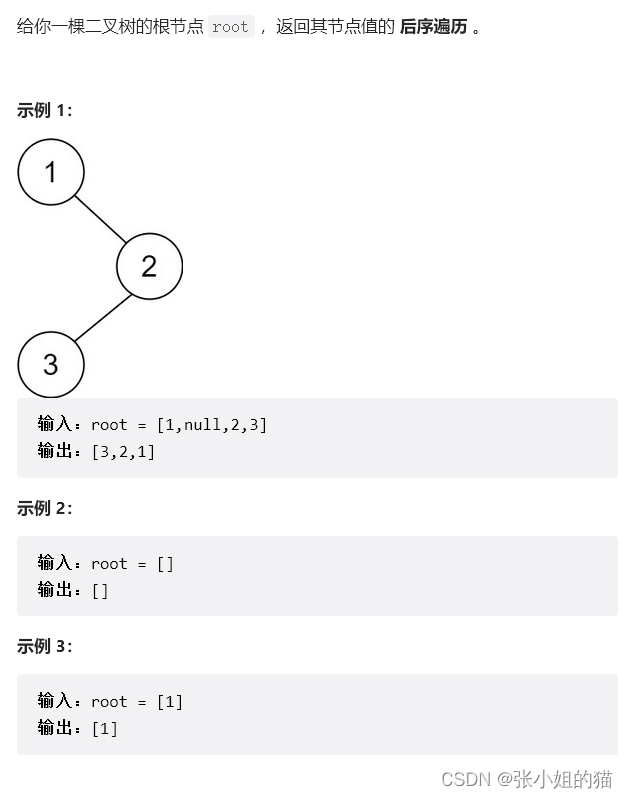
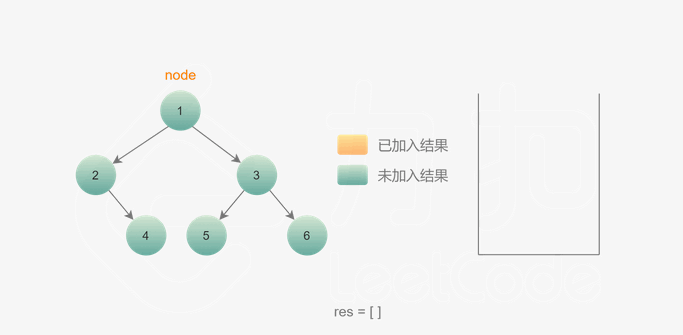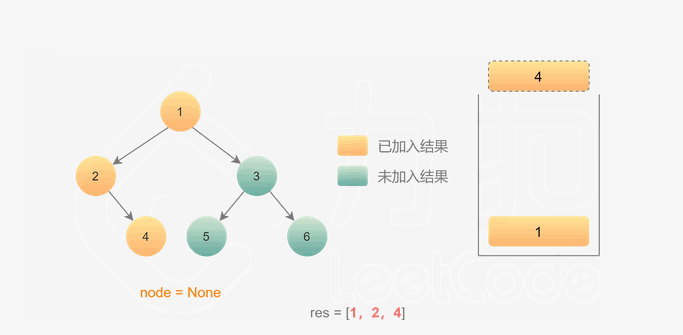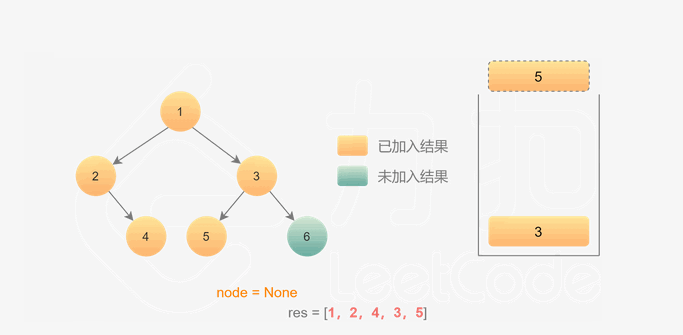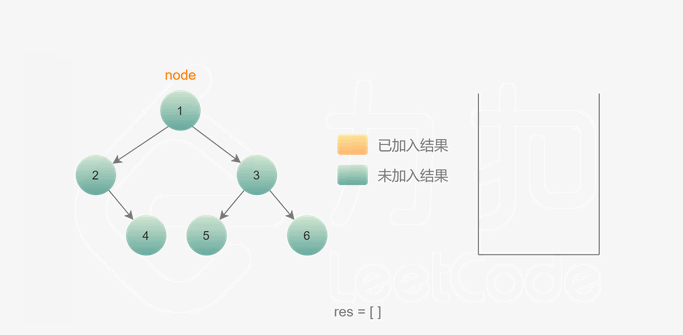
思路：

1. 和前序中序不一样，访问方式：左子树 —— 右子树 —— 根
2. 定义一个prev，来识别已经已经访问过的节点
3. 如果遍历完左边节点，右边节点为空or右边节点已经访问过了，则可以访问root

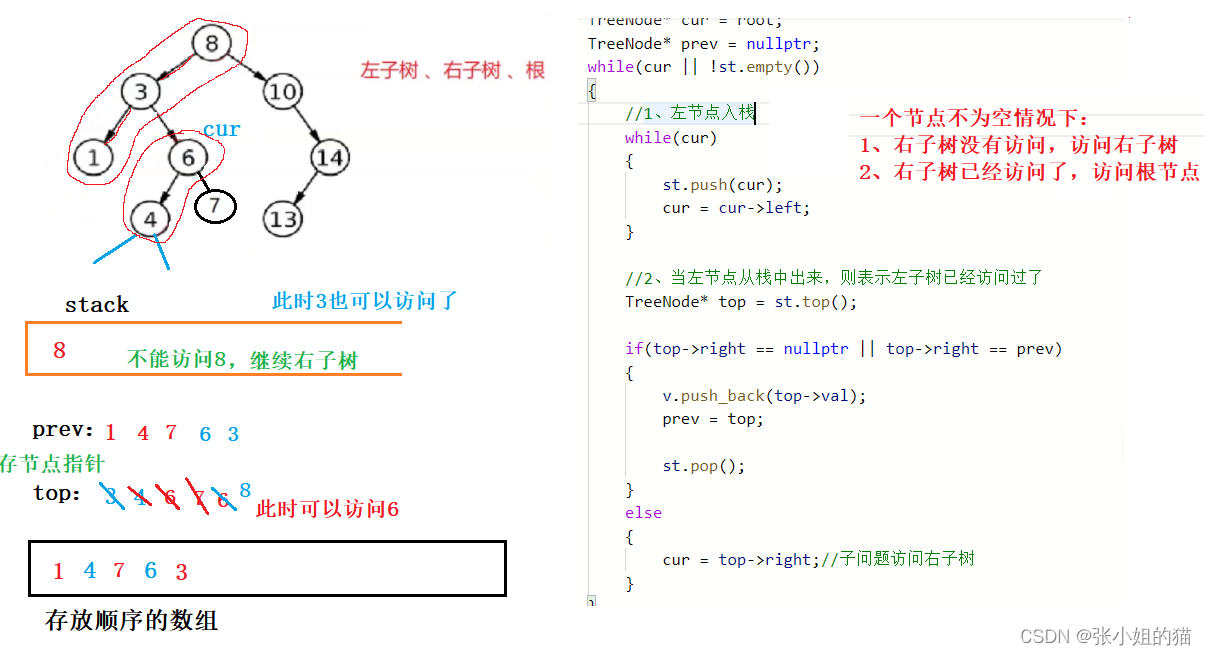
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) 
    {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode* cur = root;
        TreeNode* prev = nullptr;
        while(cur || !st.empty())
        {
            //1、左节点入栈
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }
 
            //2、当左节点从栈中出来，则表示左子树已经访问过了
            TreeNode* top = st.top();

            if(top->right == nullptr || top->right == prev)
            {
                v.push_back(top->val);
                prev = top;

                st.pop();
            }
            else
            {
                cur = top->right;//子问题访问右子树
            }
        }
        return v;
    }
};

📢写在最后

acwing永远滴神