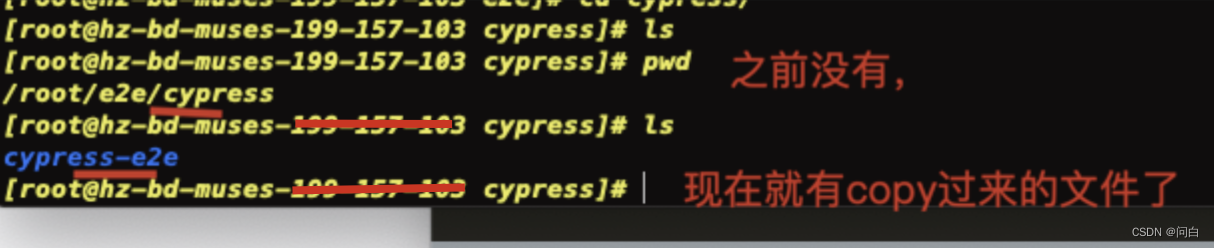
大家总喜欢搞些什么排行榜。有一说一,排行榜通常不重要,除非——比如你老板要你做一下年终总 结。
为了实现建设世界一流大学和建设世界一流学科的目标,不少大学都用各种方式提升排名:发表论文、 申请基金、提升多样性. . . 不过看起来这些并不容易,而且 US News 和 Times 这样的机构并不一定会 公正评判你的工作。因此,一些大学更聪明——自己发布排行榜,这可以使得自己的名次间接变好。比 如,通过上海某大学发布的软科排名(ARWU)作为桥梁,咖波甚至可以论证他的闵行理工学院要好于 麻省理工学院:
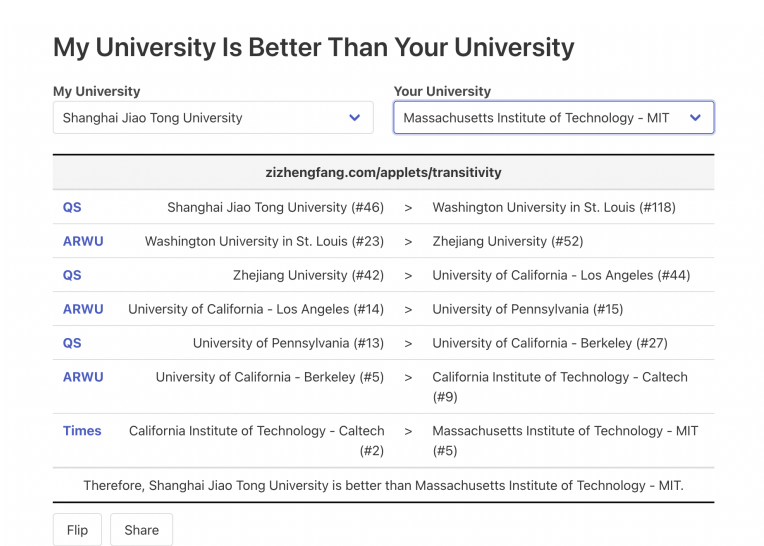
Zizheng Fang
当然,除了咖波的工作面试里,上面这种比较最多出现在知名公众号二月十三里。与此同时,咖波想知 道在这种比较方式下排名会发生什么样的变化。考虑 m 个排行榜中的 n 所大学,为简单起见,所有大 学都用一个从 1 到 n 的数字编号来表示。这里,咖波定义学校 x 直接好于学校 y,当且仅当存在一份 大学排名中学校 x 排在学校 y 前面。如果咖波认为学校 x 好于学校 y,当且仅当存在一个学校的序列 {s1, s2, ..., sk} (k ≥ 2),满足:
• s1 = x, sk = y;
• ∀i ∈ {1, 2, . . . , k − 1}, 学校 si 直接好于学校 si+1。
对于每一所学校,咖波想知道这所学校好于多少所其他学校。

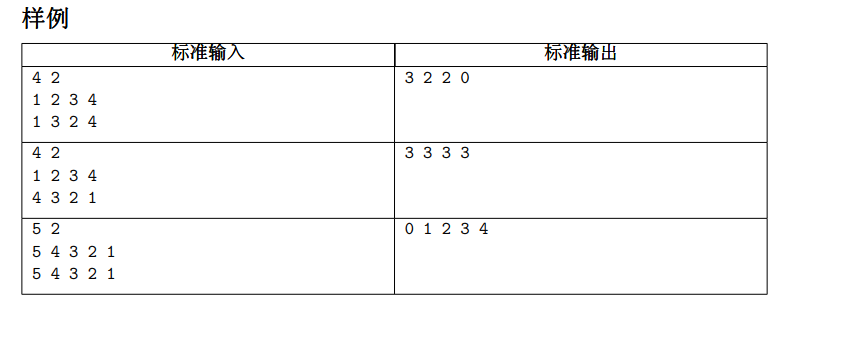
因为附有中文题面,题目大意不再介绍。
解题思路:
一种比较常见的做法就是运用图论的知识,缩点+拓扑。这里要介绍的是一种比较新颖的做法(好吧,其实主要是我自己太懒,不想写那么长的代码)。具体思路如下:
对于每一个榜单,每次从前往后遍历所有榜单的同一个位置,我们会发现一个神奇的事情,如果当前遍历到了第i列(i从1开始,所有榜单的同一个位置构成一列),并且你发现在你遍历这前i列的过程中只出现了i个不同的数,说明什么?,从上次划定的边界开始到当前列,新增的学校只在这部分区域中出现,这些学校一定不会在后面的列中出现了,也就是说这些新增的学校在这部分区域内形成了一个环,说明这些新增的学校有着相同的答案=n-上次划定的边界,至于我们反复提到的边界是啥?当我们遇到上述这种情况的时候,比如说是在第i列遇到了这种情况,那么我们就像边界划为i+1,我们每次将新增的学校放入一个队列中,每次遇到这种情况用队列中的学校编号更新答案,然后将队列清空。
上代码:
#include <bits/stdc++.h>
using namespace std;
const int N=5e5+10;
int n,m;
vector<int>a[N];
bool vis[N];
int ans[N];
int main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
int x;
cin>>x;
a[i].push_back(x);
}
}
int num=0;
queue<int>q;
for(int i=0,las=1;i<n;i++)
{
for(int j=1;j<=m;j++)
if(!vis[a[j][i]])
{
vis[a[j][i]]=1;
num++;
q.push(a[j][i]);
}
if(num==i+1)//代码中的列是从0开始的,所以是i+1
{
while(q.size())
{
int x=q.front();
q.pop();
ans[x]=n-las;
}
las=num+1;//更新边界
}
}
for(int i=1;i<=n;i++)
cout<<ans[i]<<" ";
return 0;
}