文章目录
- 位图的概念
- 位图的实现
- 布隆过滤器
- 布隆过滤器的查找
- 布隆过滤器的删除
- 布隆过滤器的优点
- 布隆过滤器的实现
本篇实现的是位图和应用
位图的概念
下面有这样的场景:给定40亿个数,现在要找这当中的一个数,如何寻找?
- 遍历,一个一个比对
- 排序+二分查找
- 位图
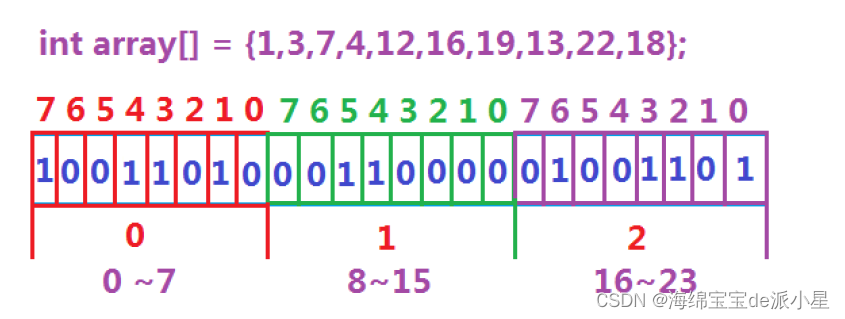
如何用位图解决?基本逻辑如下
在使用位图前,要先明确计算机中的大小是如何计算的
1 Byte = 8 Bits
1 KB = 1024 Bytes
1 MB = 1024 KB
1 GB = 1024 MB
也就是说,1GB大概是10亿个字节
那么在这个情景下,很明显,哪怕这40亿个数都不一样,也仅仅占用了40亿个比特位,也只是500MB左右的量级
位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的
位图的实现
#pragma once
#include <iostream>
#include <vector>
using namespace std;
// N是要存储的元素个数
template<size_t N>
class bitmap
{
public:
// 构造函数
bitmap()
:_size(0)
{
size_t size = (N / 8) + 1;
_map.resize(size, 0);
}
~bitmap()
{
_map.clear();
}
// 插入元素
void set(size_t x)
{
// 找到这个元素属于的下标
size_t i = x / 32;
// 找到这个元素所属的比特位
size_t j = x % 32;
// 把这个元素标记一下
_map[i] |= (1 << j);
_size++;
}
// 删除元素
void reset(size_t x)
{
// 找到元素下标和比特位
size_t i = x / 32;
size_t j = x % 32;
// 把这个元素置0
_map[i] &= ~(1 << j);
_size--;
}
// 判断一个值在不在位图里面
bool test(size_t x)
{
// 找到它在位图的位置
size_t i = x / 32;
size_t j = x % 32;
return _map[i] & (1 << j);
}
// 查看
void Print()
{
cout << "size:" << _size << endl;
for (int i = 0; i < 100; i++)
{
if (test(i))
cout << i << " ";
}
cout << endl;
}
private:
vector<int> _map;
size_t _size;
};
位图的实现逻辑其实很简单,只是运用了一个位运算就可以解决了
位图的运用
- 快速查找某个数据是否在一个集合中
- 排序 + 去重
- 求两个集合的交集、并集等
- 操作系统中磁盘块标记
布隆过滤器
什么是布隆过滤器?
简单来说,布隆过滤器是一种巧妙的概率型数据结构,它的优点主要体现在高效地插入和查询,用来表明这个东西一定不存在或者可能存在的问题,它的底层是用多个哈希函数,将一个数据映射到多个位图中,这样可以提高查找效率,也能节省空间
布隆过滤器的查找
布隆过滤器的底层如上面所示,因此被映射的位置的比特位是1,因此在寻找的时候就根据不同的哈希函数计算出对应的哈希值,再用每个对应的哈希值来看是否为0,如果这三个中有一个是0,那么就说明这个值不存在
布隆过滤器的误判情况
有下面的误判情况,比如说,现在有三个哈希函数,如果去这三个哈希函数对应的哈希值来到布隆过滤器中查找,会出现一些情况:如果有一个为0,那么绝对可以说明这个值是不存在的,但是反之却不能这么说,如果全都存在,也依旧会有不存在的可能,可能程序计算出的哈希值已经被映射过了,这样去对应得到的结果也依旧是存在的,但是很显然它本身是不存在的,所以布隆过滤器是存在误判的现象的
因此,使用合适的哈希函数可以尽可能的把误判的情况减少,减少它出现的概率,但是想要真正的出现一次都不进行误判还是有一定的难度,只能是尽可能的降低这种情况出现的概率与可能性
布隆过滤器的删除
布隆过滤器的删除其实是有些许问题的,这个问题其实很好想明白,如果此时的测试用例就是上面出现误判的这个测试用例,那么此时如果这个东西不存在,但是通过搜索发现它本身在这个过滤器中存在,并且还把它删除,那么就意味着这会出现其他映射值的问题,哪怕是这个值本身是存在的,直接贸然把位图中对应的值置为0也会出现很多问题
对于这样的情况,实际上还是有解决方案的,一个经典的解决方案就是使用引用计数的方法,在每个值的下面多一个计数器,当插入数据的时候就对它加1,删除数据的时候就对它减1,这样可以进行一定程度的优化,但是也并不能真正的解决误判对布隆过滤器带来的影响
布隆过滤器的缺陷
- 不能确定这个元素是不是真正的存在于布隆过滤器中
- 可能存在计数回绕的问题
布隆过滤器的优点
- 布隆过滤器的优点还是很明显的,它的优点主要就是体现在查找相当快,只需要根据哈希函数计算出哈希值然后进行比对就可以了
- 哈希函数相互没有关系,方便硬件进行运算
- 布隆过滤器不需要存储元素本身,它存储的是这个元素所对应的哈希值,因此对于隐秘数据可以做很好的保护
- 如果可以接受一定程度的误判的情况下,过滤器还是比其他的数据结构的比对要方便很多
- 数据量很大的时候,布隆过滤器可以表示全集
- 使用同一组散列函数的布隆过滤器可以进行交并差集运算
布隆过滤器的实现
#pragma once
#include <bitset>
#include <string>
using namespace std;
struct BKDRHash
{
size_t operator()(const string& key)
{
// BKDR
size_t hash = 0;
for (auto e : key)
{
hash *= 31;
hash += e;
}
return hash;
}
};
struct APHash
{
size_t operator()(const string& key)
{
size_t hash = 0;
for (size_t i = 0; i < key.size(); i++)
{
char ch = key[i];
if ((i & 1) == 0)
{
hash ^= ((hash << 7) ^ ch ^ (hash >> 3));
}
else
{
hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));
}
}
return hash;
}
};
struct DJBHash
{
size_t operator()(const string& key)
{
size_t hash = 5381;
for (auto ch : key)
{
hash += (hash << 5) + ch;
}
return hash;
}
};
template<size_t N,
class K = string,
class HashFunc1 = BKDRHash,
class HashFunc2 = APHash,
class HashFunc3 = DJBHash>
class BloomFilter
{
public:
void Set(const K& key)
{
size_t hash1 = HashFunc1()(key) % N;
size_t hash2 = HashFunc2()(key) % N;
size_t hash3 = HashFunc3()(key) % N;
_bs.set(hash1);
_bs.set(hash2);
_bs.set(hash3);
}
bool Test(const K& key)
{
// 判断不存在是准确的
size_t hash1 = HashFunc1()(key) % N;
if (_bs.test(hash1) == false)
return false;
size_t hash2 = HashFunc2()(key) % N;
if (_bs.test(hash2) == false)
return false;
size_t hash3 = HashFunc3()(key) % N;
if (_bs.test(hash3) == false)
return false;
// 存在误判的
return true;
}
private:
bitset<N> _bs;
};