训练深层神经网络是十分困难的,特别是在较短的时间内使他们收敛更加棘手。
本节将介绍批量规范化(batch normalization),这是一种流行且有效的技术,可持续加速深层网络的收敛速度。 再结合在 将介绍的残差块,批量规范化使得研究人员能够训练100层以上的网络。
1. 批量归一化

当神经网络特别深的时候,数据是在下面,损失函数在上面,会出问题如下:
在自动求梯度有提过,正向的时候,数据从下面一直往上计算,执行forward函数,但是在进行backward时,是从上面向下传,因此会出现梯度在上面比较大,越到下面梯度越容易变小,n个很小的数相乘,乘到最后梯度就会变得比较小。越靠近数据,那些层的梯度会变小。
上面层的梯度比较大,那么每次更新的时候,上面的梯度会不断更新,而下面层梯度小,对权重的更新就比较小,这样会导致,上面的很快会收敛,下面的会收敛得比较慢。
下面的是尝试抽取底层的特征,如局部的,边缘,很简单的纹理等信息,上面的则是抽取高层语义的信息
因为上面的会收敛得快,训练得更快,那么当下面的收敛得比较慢的时候改变了,使得上面的权重要重新学习。
2. 核心想法

3. 批量归一化层

而对于卷积层,是作用在通道维上面。
对每一个像素而言,如果有100个通道,其实是可以看成一个长为100维的向量,可以认为这个向量是这个像素的特征。就可以认为,对于一个有高宽的输入来说,每一个像素就是一个样本,所以对于卷积层来说,假设输入是 批量大小 x 高 x 宽 x通道数的话,那么样本数就是批量大小 x 高 x 宽,就是整个批量里面所有的像素都是一个样本。

从另一个角度来想,每个通道是不同的模式/特征,那么同一像素所有通道自然就是该信号的所有特征了。
解释图中的等价(和批量归一化无关):所以 1* 1的卷积层的作用等价于:如图,把输入拉成一个 9 * 3(9是样本数,3是特征数)的二维矩阵,和一个 3 * 2的矩阵相乘(1* 1的卷积层),而这两个矩阵相乘就可以看做是全连接。
图中,批量大小为1,如果要对经过1*1 卷积层的输出进行批量归一化就是,我们在每个输出通道的3 * 3个元素上同时执行每个批量规范化。 因此,在计算平均值和方差时,我们会收集所有空间位置的值,然后在给定通道内应用相同的均值和方差,以便在每个空间位置对值进行规范化。(可以理解为对一个 9 * 2的二维矩阵,每一列做均值和方差)
4. 批量归一化在做什么?
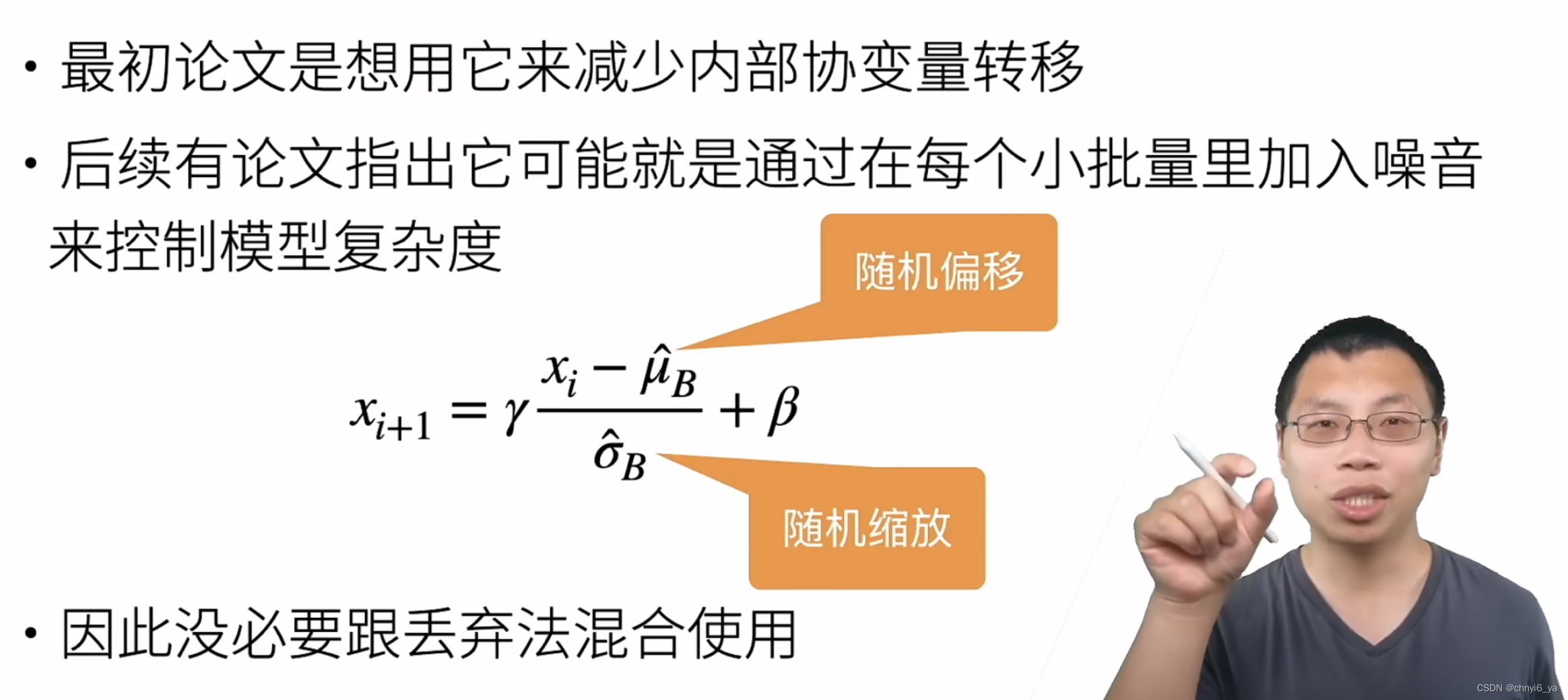
解释“随机”:因为选取批量时,是从所有输入中随机取样,每次选择的批量内容是随机的,因此取平均和方差也是随机的。
5. 总结
- 批量归一化固定小批量中的均值和方差,然后学习出适合的偏移和缩放
- 可以加速收敛速度,但一般不改变模型精度
- 把每一层的输入都放在一个差不多的分布中,用统一的学习率去训练
Batch Normalization是解决当输入数据的分布发生变化后,如何减少对深层网络结构的影响(参数的影响)。那么通过计算方差和均值,和参数γ和β的调整,使得不同分布的输入数据可以保持一定的数值稳定性,但又保持了数据的特征。(个人浅显理解,欢迎批评指正)