数据结构之红黑树的生成、添加以及删除详解（附代码）

news2024/10/6 14:27:54

一，红黑树的来历

红黑树，首先是一个二叉树，对于二叉树，人们为了提升它的搜索效率，降低时间复杂度，创造出了二叉搜索树，把时间复杂度降低为对数级（LOGn)，但是会出现一些极端情况，如下面：

 上面也是一棵二叉搜索树，符合二叉搜索树的性质，但它已经褪变成一个链表了，时间复杂度为Ｏ(n)，常数级．所以为了解决这个问题，又创造出来平衡二叉树，平衡二叉树我在前面的文章里已经详细介绍过了，时间复杂度为对数级O(logn)，但是平衡二叉树在添加和删除元素时，为了保持左右子树的平衡，有大量的旋转操作．比较影响效率．于是，红黑树出场了，它相对平衡二叉树来说，减少了旋转次数，因为它没有严格的左右子树平衡的要求，它只需要做到黑色平衡就可以了，所以旋转次数减少的同时，时间复杂度没有增加，这就是红黑树．

二，红黑树的定义

要了解红黑树，那必须得了解它的五大特性：

1，所有结点非红即黑；（这个就不必细说了）

２，根必须是黑色的；

３，所有叶子结点都是黑色的；（这里的叶子结点是指的NIL空结点，一会我会在图里说明）

４，每个红色结点的子结点必须是黑色的；（从根到每个叶子结点的所有路径上不能出现两个连续的红色结点）

５，从任一结点出发，到其每个叶子结点的路径上，都会经过相同数目的黑色结点（这里就是我上面提到过的黑色平衡）

 上图中，根结点５必须是黑色的

２，４，６，８结点必须是黑色的，不然会产生连续的红色结点，违背第４条规则

从根结点５号出发，到任意叶子结点NIL，所经过的黑色结点数量是一样的，都经过了两个黑色结点，从３号出发，到NIL点，都经过了一个黑色结点

所有的NIL点都是黑色的（在红黑树中，大家习惯把NIL结点称为叶子结点）

三，红黑树的生成

 １，算法思路

和平衡二叉树一样，我们往一棵空的红黑树当中添加元素，这里要特别注意（规定添加结点时，这个被添加的结点的颜色必须是红色的），如果为空树，直接添加为根结点，因为又有规定，根结点必须为黑色，所以要把添加进去的红色根结点变为黑色根结点．

继续添加，判断树不为空，然后从根结点开始，和添加的结点的值比较大小，如果值比根结点大则指向根结点的右孩子，反之，则是左孩子．然后继续和右孩子或者左孩子比较大小，直到找到空指针为止，然后把这个结点加上去．注意：如果是平衡树，这时候应该是要更新平衡因子，判断树是否失衡，如果失衡就需要调整．但是红黑树没有平衡因子，此时，它只判断加入该结点后，该树是否还符合红黑树的五大特性

因为加入的结点为红色的，所以不会影响黑色平衡，只对第４条：不能出现连续的红结点有影响，所以这时就要判断，加入的结点的父亲结点是不是红色，如果父亲结点为黑色，那就不需要调整，如果父亲结点为红色，那就要调整（具体怎么调整我下面马上会讲），直到调整到该树符合五大特性为止．然后继续添加结点，直到结束．

２，调整

我总结了一下，一共有以下６种情况需要调整：

上面４种情况，也不用强记怎么变的，看过我上一篇平衡二叉树的，应该都知道 

首先判断添加的结点的父亲结点，是爷爷结点的左孩子还是右孩子，左孩子记Ｌ，右孩子记Ｒ．然后再判断这个添加的结点是父亲结点的左孩子还是右孩子，左孩子记Ｌ，右孩子记Ｒ．

在三个结点中（添加的结点，添加的结点的父亲结点，添加的结点的爷爷结点），中间值的点变成黑色结点，做为这棵小树的根结点，另外两个结点按规则分别为左右孩子且都为红色结点，最后一个结点按排序树的规则也可以推断出放的位置．

最后两种：

 添加的结点，在有红色叔叔结点的时候，不需要调整，只需要变色

只有在没有叔叔结点的时候，才需要进行最上面的４种调整

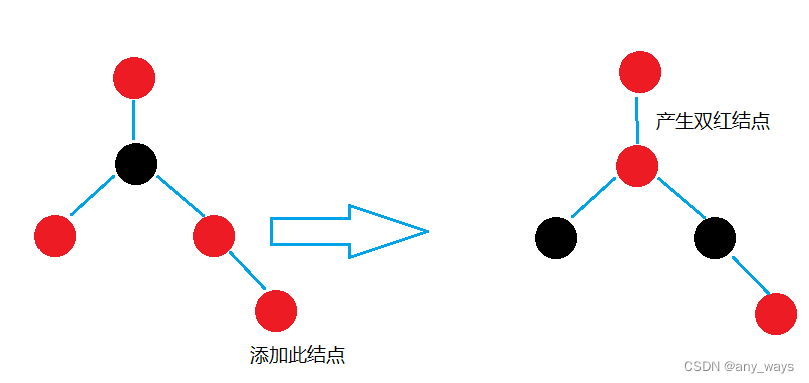
 这里还有一个特别重要的，上面两种变色的类型中，如果添加的结点的爷爷是根结点，那么根结点要变成黑色结点（第二特性），如果不是根结点，而且爷爷的父亲结点也是红色，那么就会产生双红结点，所以，必须以爷爷结点做为添加的结点，递归去判断上层有没有双红节点，直到根结点为止．

四，红黑树的删除操作

红黑树的平衡是黑色平衡，也就是说，如果删除的结点是红色，它是不需要调整的

红黑树的删除有以下三种情况：

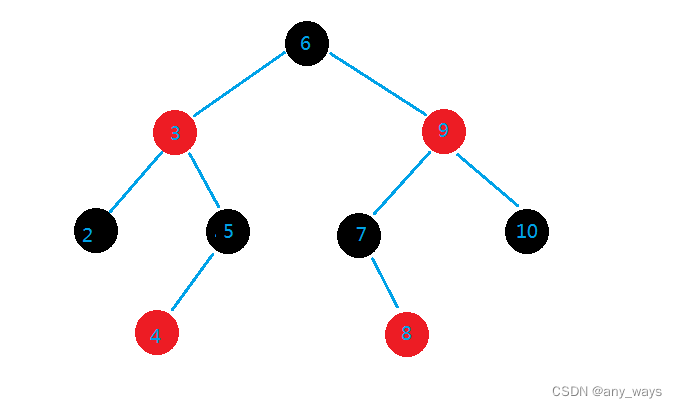
１，删除的结点有左右两个孩子 

比如，上面我们要删除结点６，那么我们先找到结点６前驱的最大值，或者后继的最小值，这里我们就拿后继的最小值７，然后把结点７的值赋给结点６，然后再删除结点７就可以了

２，删除的结点只有一个孩子

如上图，结点５和７，都只有一个孩子，这种情况，直接删除，然后孩子顶替它的位置，为了保证平衡，孩子的颜色要变为黑色

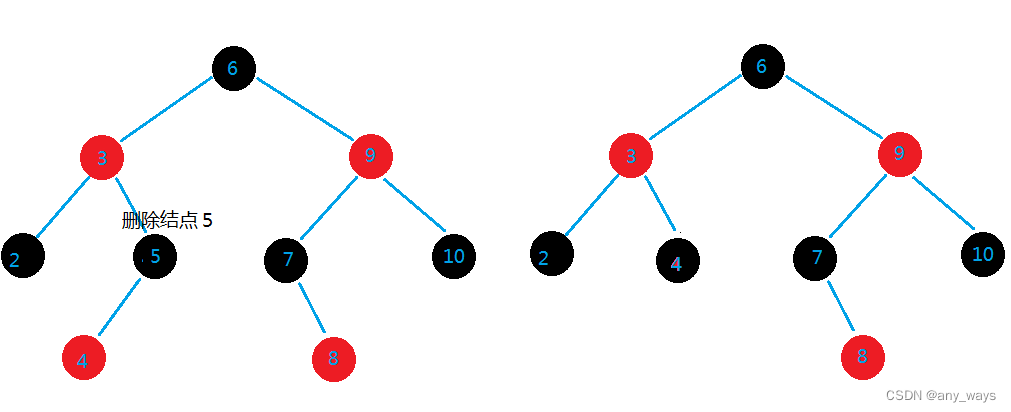上图：如果结点５为黑色，那么结点４必为红色 

 ３，删除的结点，是叶子结点，没有孩子

这种情况也是直接删除，不过如果这个结点是黑色的话，是需要调整的，调整的方法和这个要删除的黑色结点的兄弟结点有关，根据它兄弟结点的状态，有以下三种情况：

（前提：兄弟结点必须是黑色，如果是红色，兄弟结点是父亲结点的左子树就以父亲结点为基点ＬＬ调整，反之则ＲＲ调整，调整完后，兄弟结点就变成了黑色）

１，兄弟结点没有孩子

到这里，我估计有人会说了，如果这里的９结点本来就是黑色，那不是就不平衡了．

是的，如果父亲结点本来为黑色，那么就是父亲结点为基点，再找它的兄弟结点，然后判断兄弟结点的三个情况，继续调整．

２，兄弟结点有一个孩子

如果兄弟是父亲结点的左孩子，兄弟结点有一个左孩子，那么此时就以父亲结点为基点ＬＬ调整，如果兄弟结点的孩子是右孩子，那么就ＬＲ调整 

 如果兄弟是父亲结点的右孩子，兄弟结点有一个左孩子，那么此时就以父亲结点为基点ＲＬ调整，如果兄弟结点的孩子是右孩子，那么就ＲＲ调整 

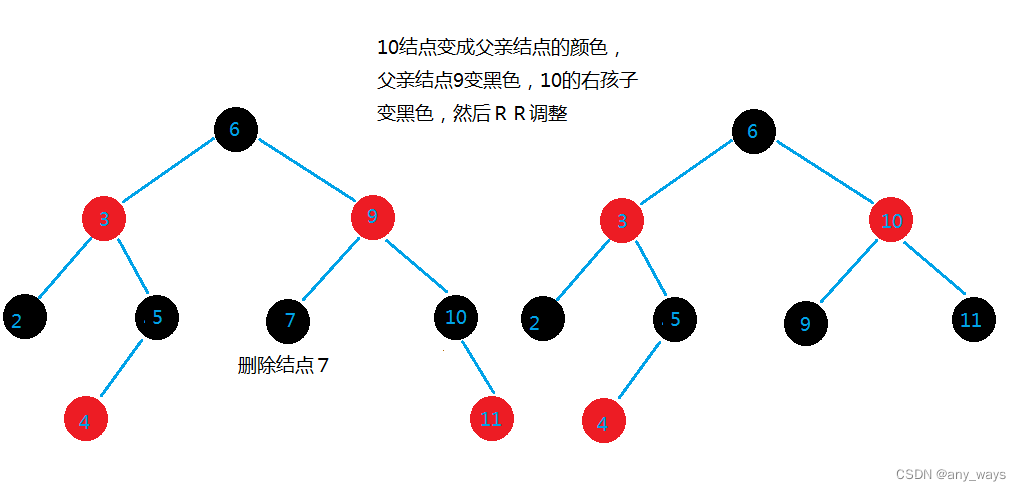
3,兄弟结点有两个孩子

此时，如果兄弟结点是父亲结点的左孩子，那么就ＬＬ调整，如果兄弟结点是父亲结点的右孩子，那么就ＲＲ调整． 

 具体的代码为：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <windows.h>

typedef struct Node{
    int data;
    char color;
    struct Node* left;
    struct Node* right;
    struct Node* parent;
}Node,*BRTree;
BRTree currentNode = NULL;
BRTree insertEle(BRTree* node, int m, BRTree parent)
{
    if(!(*node))
    {
        *node = malloc(sizeof(Node));//创建一个红色的结点，并初始化
        currentNode = *node;//保存插入的节点
        (*node)->data = m;
        (*node)->color = 'r';
        (*node)->left = NULL;
        (*node)->right = NULL;
        (*node)->parent = parent;
        if(!parent)(*node)->color = 'b';//如果这个节点是根结点，变为黑色
    }
    else
    {
        if(m < (*node)->data)//递归寻找插入点
        {
            insertEle(&(*node)->left, m, *node);
        }
        else if(m > (*node)->data)
        {
            insertEle(&(*node)->right, m, *node);
        }
        else return currentNode;//返回插入的这个结点
    }
    return currentNode;//返回插入的这个结点
}

void setLL(BRTree* T, BRTree a)
{
    BRTree b = a->left;
    if(a->parent)//如果结点不是根结点
    {
        if(a==a->parent->left)//如果该结点，是它父亲结点的左孩子
        {
            a->parent->left = b;//该结点的父亲结点的左孩子指向b
        }
        else
        {
            a->parent->right = b;//否则，该结点的父亲结点的右孩子指向b
        }
    }
    else
    {
        *T = b;//如果该结点是根结点，那么要把调整后b作为根结点
    }
    a->left = b->right;
    if(b->right)b->right->parent = a;
    b->right = a;
    b->parent = a->parent;
    a->parent = b;



}

void setRR(BRTree* T, BRTree a)
{
    BRTree b = a->right;
    if(a->parent)
    {
        if(a==a->parent->left)
        {
            a->parent->left = b;
        }
        else
        {
            a->parent->right = b;
        }
    }
    else
    {
        *T = b;
    }
    a->right = b->left;
    if(b->left)b->left->parent = a;
    b->left = a;
    b->parent = a->parent;
    a->parent = b;
}

void setLR(BRTree* T, BRTree a)
{
    BRTree b = a->left;
    BRTree c = a->left->right;
    if(a->parent)
    {
        if(a==a->parent->left)
        {
            a->parent->left = c;
        }
        else
        {
            a->parent->right = c;
        }
    }
    else
    {
        *T = c;
    }
    b->right = c->left;
    a->left = c->right;
    if(c->left)c->left->parent = b;
    if(c->right)c->right->parent = a;
    c->left = b;
    c->right = a;
    c->parent = a->parent;
    b->parent = c;
    a->parent = c;


}

void setRL(BRTree* T, BRTree a)
{
    BRTree b = a->right;
    BRTree c = a->right->left;
    if(a->parent)
    {
        if(a==a->parent->left)
        {
            a->parent->left = c;
        }
        else
        {
            a->parent->right = c;
        }
    }
    else
    {
        *T = c;
    }
    b->left = c->right;
    a->right = c->left;
    if(c->right)c->right->parent = b;
    if(c->left)c->left->parent = a;
    c->right = b;
    c->left = a;
    c->parent = a->parent;
    b->parent = c;
    a->parent = c;

}
void adjust(BRTree* T, BRTree node)//碰到双红节点后的调整
{
    int flag = 1;
    do
    {
        flag = 0;
        if(node->parent==NULL)return;
        if(node->parent->color=='r')
        {
            if(node->parent->parent->left==node->parent)//如果爷爷结点的左孩子是父亲结点
            {
                if(node->parent->parent->right && node->parent->parent->right->color=='r')//如果有叔叔结点，且为红色
                {
                    node->parent->color = 'b';//父亲结点变黑色
                    node->parent->parent->right->color = 'b';//叔叔结点变黑色
                    node->parent->parent->color = 'r';//爷爷结点变成红色
                    if(node->parent->parent==*T)node->parent->parent->color = 'b';//如果爷爷结点是根结点，那么此时要变回黑色
                    node = node->parent->parent;//结点指向爷爷结点，再递归调整
                    flag = 1;//需要再次判断，所以打开循环开关
                }
                else
                {
                    if(node->parent->left == node)//该结点是父亲结点的左孩子
                    {
                        node->parent->color = 'b';
                        node->parent->parent->color = 'r';
                        setLL(T, node->parent->parent);
                    }
                    else//该结点是父亲结点的右孩子
                    {
                        node->color = 'b';
                        node->parent->parent->color = 'r';
                        setLR(T, node->parent->parent);
                    }
                }
            }
            else
            {
                if(node->parent->parent->left && node->parent->parent->left->color == 'r')//如果有叔叔结点，且为红色
                {
                    node->parent->color = 'b';
                    node->parent->parent->left->color = 'b';
                    node->parent->parent->color = 'r';
                    if(node->parent->parent==*T)
                    {
                        node->parent->parent->color = 'b';
                    }
                    flag = 1;//需要再次判断，所以打开循环开关
                    node = node->parent->parent;//结点指向爷爷结点，再递归调整


                }
                else
                {
                    if(node->parent->left == node)
                    {
                        node->color = 'b';
                        node->parent->parent->color = 'r';
                        setRL(T, node->parent->parent);
                    }
                    else
                    {
                        node->parent->color = 'b';
                        node->parent->parent->color = 'r';
                        setRR(T, node->parent->parent);
                    }
                }
            }
        }
    }
    while(flag);

}



void swapArr(BRTree a[], BRTree b[],int len)//为了打印红黑树，写的交换数组函数，与红黑树无关
{
    int i;
    BRTree temp;
    for(i = 0; i < len; i++)
    {
        temp = a[i];
        a[i] = b[i];
        b[i] = temp;

    }
}


void printRBTree(BRTree node)//广度遍历该红黑树，并打印出来．与红黑树本身无关，无需了解
{
    BRTree a[16],b[16];
    a[0] = node;//数组a中起始元素个数１个（根结点）
    int nums = 1;//数组a中起始元素个数１个（根结点）
    int flag = 1;//判断数组a中，有没有元素
    int i;
    int blank = 20;
    char str[100] = "";
    int c1 = 10;
    int c2 = 5;
    int c3 = 3;
    int c4 = 2;
    while(flag)
    {
        flag = 0;
        int j = 0;
        blank--;
        printf("%*s",blank--,"");

        for(i = 0; i < nums; i++)
        {
            if(a[i])
            {
                HANDLE hConsole = GetStdHandle(STD_OUTPUT_HANDLE);
                if(a[i]->color == 'r')
                {
                    SetConsoleTextAttribute(hConsole, 0xC );
                }
                else if(a[i]->color == 'b')
                {
                    SetConsoleTextAttribute(hConsole, 2 );
                }

                printf("%d",a[i]->data);
                SetConsoleTextAttribute(hConsole, 0xF );
                if(nums==2)printf("%*s",c1," ");
                if(nums==4)printf("%*s",c2," ");
                if(nums==8)printf("%*s",c3," ");
                if(nums==16)printf("%*s",c4," ");
                if(a[i]->left)
                {
                    flag = 1;
                    b[j++] = a[i]->left;
                    if(nums==1)strcat(str, "/      ");
                    if(nums==2)strcat(str, "/  ");
                    if(nums==4)strcat(str, "/ ");
                    if(nums==8)strcat(str, "/ ");
                }
                else
                {
                    b[j++] = 0;
                    if(nums==1)strcat(str, "      ");
                    if(nums==2)strcat(str, "    ");
                    if(nums==4)strcat(str, "   ");
                    if(nums==8)strcat(str, "  ");
                }
                if(a[i]->right)
                {
                    flag = 1;
                    b[j++] = a[i]->right;
                    if(nums==1)strcat(str, "\\        ");
                    if(nums==2)strcat(str, "\\        ");
                    if(nums==4)strcat(str, "\\   ");
                    if(nums==8)strcat(str, "\\  ");
                }
                else
                {
                    b[j++] = 0;
                    if(nums==1)strcat(str, "         ");
                    if(nums==2)strcat(str, "         ");
                    if(nums==4)strcat(str, "    ");
                    if(nums==8)strcat(str, "  ");
                }
            }
            else
            {
                if(nums==2)printf("%*s",c1+1," ");
                if(nums==4)printf("%*s",c2+1," ");
                if(nums==8)printf("%*s",c3+1," ");
                if(nums==16)printf("%*s",c4," ");
                b[j++] = 0;
                b[j++] = 0;
                if(nums==1)strcat(str, "            ");
                if(nums==2)strcat(str, "        ");
                if(nums==4)strcat(str, "      ");
                if(nums==8)strcat(str, "    ");

            }

        }
        nums*=2;
        printf("\n");
        blank--;
        printf("%*s",blank--,"");
        printf(str);
        printf("\n");
        memset(str,0, sizeof(str));
        int len = sizeof(a)/sizeof(a[0]);
        swapArr(a,b,len);
    }
}

void CreatRBTree(BRTree* node)
{
    int m=1;
    while(m)
    {
        printf("请输入要添加的结点的值并以0结束:>");
        scanf("%d",&m);
        if(m==0)break;
        BRTree A = insertEle(node, m, *node);//添加元素
        adjust(node, A);//判断并调整
        printRBTree(*node);

    }
}

BRTree Successor(BRTree T, BRTree a)//寻找后继点，即右孩子中的最小值结点
{
    if(a==NULL)
    {
        return NULL;
    }
    else
    {
        BRTree p = a->right;
        while(p->left)
        {
            p = p->left;
        }
        return p;
    }
}

BRTree FindNode(BRTree T, int a)//根据提供的数值，寻找树中对应的结点
{
    while(T)
    {
        if(T->data == a)
        {
            return T;
        }
        else if(T->data > a)
        {
            T = T->left;
        }
        else
        {
            T = T->right;
        }
    }
    printf("没有找到你要删除的数据！！");
    return NULL;
}
//删除节点后的调整
void modify(BRTree *T, BRTree x)
{
    //删除的结点颜色是黑色，才需要调整
    while(x->color=='b')
    {
        if(x==x->parent->left)//如果要删除的结点是父亲结点的左孩子
        {
            BRTree rnode = x->parent->right;//那么兄弟结点为父亲结点的右孩子
            if(rnode->color == 'r')//如果兄弟结点为红色，那么需要调整，是右孩子就ＲＲ调整
            {
                rnode->color = 'b';
                x->parent->color = 'r';
                setRR(T,x->parent);
                //找到真正的兄弟结点
                rnode = x->parent->right;//调整完成后，更新兄弟结点
            }
            //情况一：
            if(rnode->left==NULL&&rnode->right==NULL)//兄弟结点没有孩子
            {
                rnode->color = 'r';
                x = x->parent;//焦点指向它的父亲，等待下一轮判断，如果它父亲的颜色为红色，则不会进入循环
            }
            else
            {
                //情况二和三
                if(rnode->right==NULL)
                {
                    rnode->left->color = x->parent->color;
                    x->parent->color = 'b';
                    x->color = 'r';
                    setRL(T, x->parent);
                }
                else
                {
                    rnode->color = x->parent->color;
                    x->parent->color = 'b';
                    rnode->right->color = 'b';
                    x->color = 'r';
                    setRR(T, x->parent);
                }
            }
        }
        else
        {
            BRTree rnode = x->parent->left;
            if(rnode->color == 'r')
            {
                rnode->color = 'b';
                x->parent->color = 'r';
                setLL(T,x->parent);
                //找到真正的兄弟结点
                rnode = x->parent->left;
            }
            if(rnode->left==NULL&&rnode->right==NULL)//兄弟结点没有孩子
            {
                rnode->color = 'r';
                x = x->parent;
            }
            else
            {
                if(rnode->left==NULL)
                {
                    rnode->right->color = x->parent->color;
                    x->parent->color = 'b';
                    x->color = 'r';
                    setLR(T, x->parent);
                }
                else
                {
                    rnode->color = x->parent->color;
                    x->parent->color = 'b';
                    rnode->left->color = 'b';
                    x->color = 'r';
                    setLL(T, x->parent);
                }
            }
        }
    }
    x->color = 'b';
}
//删除结点
void DelNode(BRTree *T, int b)
{
    if(*T==NULL)return;
    BRTree a = FindNode(*T, b);
    if(a->left && a->right)//要删除的结点，既有左孩子，又有右孩子
    {
        BRTree temp = Successor(*T, a);//选择该结点，左子树中的最大值，或者右子树中的最小值．作为替换结点
        a->data = temp->data;//找到替代点，并把值拷备过来
        a = temp;//把删除对像转向替代点
    }
    //要删除的结点，有一个孩子的情况
    BRTree replace = a->left==NULL?a->right:a->left;//这个孩子的地址
    if(replace!=NULL)
    {
        replace->parent = a->parent;
        if(a->parent==NULL)
        {
            *T = replace;
        }
        //用replace替换要删除的结点
        else if(a->parent->left == a)
        {
            a->parent->left = replace;
        }
        else
        {
            a->parent->right = replace;
        }
        if(a->color =='b')
        {
            modify(T, replace);//调整
        }
        //置空，并释放内存
        a->left = a->parent = NULL;
        free(a);
    }
    //replace为空，说明该删除点，没有孩子
    else
    {
        modify(T, a);
        //直接删除该结点，关释放内存
        if(a==a->parent->left)a->parent->left=NULL;
        else a->parent->right = NULL;
        a->left = a->parent = NULL;
        free(a);
    }


}
int main()
{
    int input;
    BRTree T=NULL;
    CreatRBTree(&T);
    while(input)
    {
        printf("请输入你要删除的元素，并以0结束:>");
        scanf("%d",&input);
        if(input==0)break;
        DelNode(&T, input);
        printRBTree(T);
    }
    return 0;
}

运行效果：

 

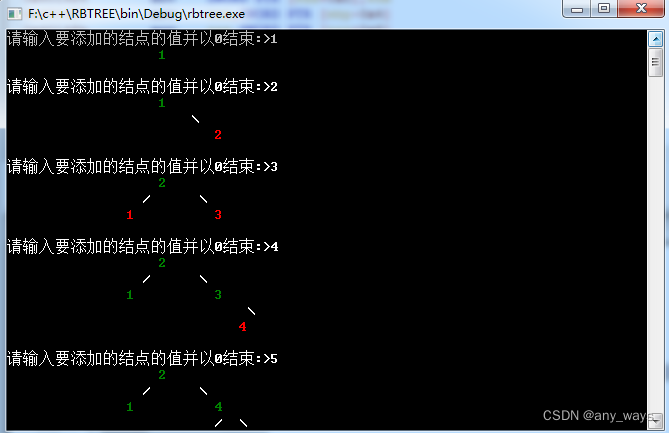
删除的效果：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/125633.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

zookeeper之基本使用及实现分布式锁

zookeeper之基本使用及实现分布式锁

写在前面 本文一起看下zk的基本用法。 安装 。 1&#xff1a;数据结构 采用类似于linux系统的文件系统存储结构&#xff0c;但不同于Linux系统文件&#xff0c;zk每个节点都可以存储数据&#xff0c;结构如下图&#xff1a; 节点类型分为如下四种&#xff1a; PERSISTENT&…
阅读更多...
RK3568平台开发系列讲解（设备驱动篇）中断下文之tasklet的使用

RK3568平台开发系列讲解（设备驱动篇）中断下文之tasklet的使用

🚀返回专栏总目录 文章目录 一、tasklet 的概念二、tasklet 参考步骤沉淀、分享、成长，让自己和他人都能有所收获！😄 📢我们一般将中断分为上下两个部分，分为上半部，下半部。上半部完成有严格时限的工作（必须），例如回复硬件等，这些工作都是在禁止其他中断情况下进…
阅读更多...
汽车相关概念记录

汽车相关概念记录

目录 一、汽车电路相关概念 1.1、两个电源 1.2、单线制 1.3、低压直流供电 1.4、常电与ACC 1.4.1、大众ACC供电开关 1.4.2、奥迪ACC开关 二、电子电路 2.1、三极管 2.1.2、截止状态 2.1.3、放大区 2.1.4、饱和区 2.1.4、实例分析 一、汽车电路相关概念 1.1、两个电…
阅读更多...
CIO40— 2022 行平常心，做自由人 (3年之约已满)

CIO40— 2022 行平常心，做自由人 (3年之约已满)

今天的天空依然很蓝。认识还是在那个不戴口罩的夏天。 感谢IT行业给了我们帮助。 IT将交流植根于微信群&#xff0c;微信群既是信息的集散地&#xff0c;也是良好实践的方案池。在工作中碰到的问题&#xff0c;只要在IT微信群中求助&#xff0c;大家都是知无不言&#xff0c…
阅读更多...
C# 异步编程

C# 异步编程

一 异步编程 1 异步 asynchronize 2 主要解决的事情是 ① 等待一些耗时的任务&#xff08;特别是文件&#xff0c;网络操作&#xff09;而不阻塞当前任务&#xff1b; ② 异步编程提高响应能力&#xff08;特别是UI&#xff09; 开始一个任务后&#xff0c;让任务在离感应线…
阅读更多...
机器学习：图文详细总结马尔科夫链及其性质(附例题分析)

机器学习：图文详细总结马尔科夫链及其性质(附例题分析)

目录0 写在前面1 从一个实例出发2 马尔科夫链3 马氏链的基本性质4 C-K方程5 平稳状态分布6 遍历性与例题分析0 写在前面 机器学习强基计划聚焦深度和广度&#xff0c;加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理&#xff1b;“广”在分析多个机器…
阅读更多...
canopen4.0-canfestiva移植以及同步帧发送

canopen4.0-canfestiva移植以及同步帧发送

1.canfestival移植入 工程包： 一、canfestival系列教程之程序移植 1.1、首先准备一个hal工程 ，cubmx --------------RCC配置 -----------SYS配置 ----------时钟配置 -----canopen定时器配置（开启中断） --------------can配置波特率，接收中断
阅读更多...
CSS3知识点精学

CSS3知识点精学

CSS3 被拆分为"模块"。旧规范已拆分成小块&#xff0c;还增加了新的。 一些最重要 CSS3 模块如下&#xff1a; 选择器盒模型背景和边框文字特效2D/3D转换动画多列布局用户界面css引入方式 内嵌式&#xff1a;CSS写在style标签中&#xff0c;style标签虽然可以写在…
阅读更多...
PE格式的base reloc分区

PE格式的base reloc分区

https://0xrick.github.io/win-internals/pe7/ 程序雕塑被编译之后&#xff0c;编译器假设可执行文件将会在特定1的v z基地址被加载&#xff0c;这个地址被保存在image_optional_header的imagebase成员中&#xff0c;一些地址会被计算出来然后硬编码到可执行文件中 出于各种原…
阅读更多...
malmquist指数案例分析

malmquist指数案例分析

传统的DEA模型可以反应静态的投入产出效率情况&#xff0c;但如果是面板数据&#xff0c;则需要使用malmquist指数进行研究。malmquist指数可以分析从t期到t1期的效率变化情况。Malmquist指数可分解为技术效率&#xff08;EC&#xff09;和技术进步&#xff08;TC&#xff09;&…
阅读更多...
Java高手速成│Java程序怎样和数据库对话

Java高手速成│Java程序怎样和数据库对话

从上一篇 Java高手速成│编写你第一个数据库程序 的例子中可以看出&#xff0c;Java和数据库的连接和对话离不开JDK库类&#xff0c;如java.sql包中支持数据库编程的各种API类、数据库软件DBMS、JDBC驱动软件或Java Connector以及你编写的数据库编程代码。 并且&#xff0c;在…
阅读更多...
基础不牢，地动山摇系列 ------ 软硬通吃 unity常用API

基础不牢，地动山摇系列 ------ 软硬通吃 unity常用API

&#x1f468;‍&#x1f4bb;个人主页&#xff1a;元宇宙-秩沅 hallo 欢迎 点赞&#x1f44d; 收藏⭐ 留言&#x1f4dd; 加关注✅! 本文由 秩沅 原创 收录于专栏 unity 实战系列 ⭐相关文章⭐ ——————————————————— -关于游戏剧情模式中用到的基础简单A…
阅读更多...
第01讲：Git安装及基本操作

第01讲：Git安装及基本操作

一、什么是Git 版本控制系统&#xff08;VCS&#xff09;是将『什么时候、谁、对什么文件做了怎样的修改』这样的信息以版本的形式保存并进行管理的系统。 简单来说&#xff0c;版本控制系统会去记录它所管理的文件的『历史版本』。 版本控制系统 “不是网盘&#xff0c;而胜…
阅读更多...
linux常用命令（一）-路径切换及查看

linux常用命令（一）-路径切换及查看

切换路径-cd 我们可以使用cd&#xff08;change directory&#xff0c;切换目录&#xff09;的命令来进行目录切换 常规 其命令格式为 cd [相对路径或绝对路径] 例如&#xff1a; // 使用相对路径&#xff0c;切换到postfix目录下 cd ../postfix// 使用绝对路径切换到/var/…
阅读更多...
Linux操作系统实验1——地址转换

Linux操作系统实验1——地址转换

实验要求&#xff1a; 1.在内核中先申请一个页面&#xff0c;使用内核提供的函数&#xff0c;按照寻页的步骤一步步的找到物理地址。这些步骤就相当于我们手动的模拟了mmu的寻页过程。(paging_lowmem.c) 2.通过mmap将物理内存的数据映射到一个设备文件中。 通过访问该设备就可以…
阅读更多...
美图商业化2.0：探寻多元增长曲线

美图商业化2.0：探寻多元增长曲线

【潮汐商业评论/原创】 数字化智能化浪潮正席卷而来。与此前的工业革命、信息技术革命一样&#xff0c;这场箭在弦上的“数智化革命”核心也在于技术的突破与应用。 今年以来&#xff0c;AIGC作为AI技术在内容生产领域的应用&#xff0c;迎来了全球大厂的争相布局&#xff0c…
阅读更多...
tensorflow2.x多层感知机模型参数量和计算量的统计

tensorflow2.x多层感知机模型参数量和计算量的统计

当创建了一个多层感知机模型后&#xff0c;如何调用接口获取该模型的参数量和计算量&#xff1f;首先&#xff0c;打印出模型结构&#xff0c;可通过graphviz模块实现 # 加载模型 model keras.models.load_model(modelPath) tf.keras.utils.plot_model(model, to_filemodel.p…
阅读更多...
linux ubuntu 如何自动定时备份数据库到服务器 mysql mysqldump cron

linux ubuntu 如何自动定时备份数据库到服务器 mysql mysqldump cron

linux ubuntu 如何自动定时备份数据库到服务器 mysql mysqldump cron 一、需求描述 我有一个小日记应用&#xff0c;从 2019 年到 2022 年已经出现了两次比较严重的数据丢失的情况&#xff0c;一次是服务器错误&#xff0c;一次是人为。 所以我急切需要它能自己自动备份数据库…
阅读更多...
基于servlet+jsp+mysql实现的java web校园车辆管理系统

基于servlet+jsp+mysql实现的java web校园车辆管理系统

一、项目简介 本项目是一套基于servletjspmysql实现的java web校园车辆管理系统&#xff0c;主要针对计算机相关专业的正在做毕设的学生与需要项目实战练习的Java学习者。 包含&#xff1a;项目源码、数据库脚本等&#xff0c;该项目附带全部源码可作为毕设使用。 项目都经过严…
阅读更多...
WebDAV之葫芦儿·派盘+Orgzly

WebDAV之葫芦儿·派盘+Orgzly

Orgzly 支持WebDAV方式连接葫芦儿派盘。 给大家推荐一款Android 上的笔记与 todo 待办事项相融合的应用，它通过树形结构来记录笔记，并且只需要对笔记进行 TODO 标记就能变身任务管理，十分方便。 Orgzly是一款多功能的应用，更确切地说，它是一款 org 文件编辑器。Org 和 …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023