- 寻找数组中的第k小元素
【问题描述】给定一个长度为n的整数数组nums和整数k,输出数组中的第k小元素。要求不能对数组排序,使用分治的思想求解。
【输入形式】输入的第1行中有1个数字n,表示数组的长度;第2行中有n个数字,表示数组的元素;第3行中有1个数字k。
【输出形式】输出1行中有1个数字,表示数组中的第k小元素。
【样例输入】6
3 2 1 4 6 5
2
【样例输出】2
【说明】
1<=k<=n<=10^410^-5<=nums[i]<=10^5
#include<bits/stdc++.h>
using namespace std;
int n,num[10010],k;
int findmid(int l,int r)
{
int i,numm=0;
for(i=l;i+4<=r;i+=5,numm++)
{
sort(num+l,num+l+5);
swap(num[l+numm],num[i+2]);
}
if(i<=r)
{
sort(num+i,num+r+1);
swap(num[l+numm],num[i+(r-i+1)/2]);
numm++;
}
if(numm==1) return num[l];
else return findmid(l,l+numm-1);
}
int partion(int l,int r,int p)
{
swap(num[p],num[l]);
int i=l,j=r,post=num[i];
while(i<j)
{
while(i<j && num[j]>=post) j--;
if(i<j) num[i]=num[j];
while(i<j && num[i]<=post) i++;
if(i<j) num[j]=num[i];
}
num[i]=post;
return i;
}
int find(int l,int r,int k)
{
int mid=findmid(l,r);
int p=partion(l,r,l);
int len=p-l+1;
if(len==k) return num[p];
else if(len>k) return find(l,p-1,k);
else return find(p+1,r,k-len);
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{
cin>>num[i];
//cout << num[i]<<" ";
}
cin>>k;
int ans=find(0,n-1,k);
cout << ans;
return 0;
} 2.文件压缩
【问题描述】给定一个文件,文件由n个字符组成,但他们出现的频度不相同。要求对该文件中的字符集构造哈夫曼树,并计算编码后的文件长度。
【输入形式】
输入的第1行有1个数字n,表示文件中总的字符个数。接下来1行中有n个数字,分别表示n个字符出现的频度。
【输出形式】
输出1行包含1个数字,表示使用哈夫曼编码后该文件的长度。
【样例输入】
5
20 7 10 4 18
【样例输出】
129
【样例说明】
使用哈夫曼编码后,各字符的编码长度分别为2 3 2 3 2,文件长度为2*20+3*7+2*10+3*4+2*18=129
#include<bits/stdc++.h>
using namespace std;
int n;
typedef struct huffman
{
int weight,len,parent,lc,rc;
}huff;
huff tree[110];
void hfm()
{
int i,j,p1,p2,s1,s2;
for(i=0;i<2*n-1;i++)
{
tree[i].parent=-1;
tree[i].lc=-1;
tree[i].rc=-1;
tree[i].weight=0;
}
for(i=0;i<n;i++)
{
int temp;
cin>>temp;
tree[i].weight=temp;
}
for(i=n;i<2*n-1;i++)
{
p1=-1;p2=-1;s1=1000;s2=1000;
for(j=0;j<i;j++)
{
if(tree[j].parent==-1)
{
if(tree[j].weight<s1)
{
s2=s1;
s1=tree[j].weight;
p2=p1;
p1=j;
}
else if(tree[j].weight<s2)
{
s2=tree[j].weight;
p2=j;
}
}
}
tree[p1].parent=i;
tree[p2].parent=i;
tree[i].lc=p1;
tree[i].rc=p2;
tree[i].weight=tree[p1].weight+tree[p2].weight;
}
int all=0,len;
huff s;
for(i=0;i<n;i++)
{
len=0;
s=tree[i];
while(s.parent!=-1)
{
s=tree[s.parent];
len++;
}
tree[i].len=len;
all+=tree[i].weight*tree[i].len;
}
cout << all;
}
int main()
{
cin>>n;
hfm();
return 0;
}3.切分数组
【问题描述】给定一个整数数组 nums ,将 nums 切割成若干个非空子数组,使得每个子数组最左边的数和最右边的数的最大公约数大于 1 。请求出最少可以切成多少个子数组。
【输入形式】
输入数据有两行;
第一行是数组元素个数;
第二行是数组元素;
【输出形式】
输出数据有一行,是最少子数组个数;
【样例输入】
6
2 3 3 2 3 3
【样例输出】
2
【样例说明】最优切割为 [2,3,3,2] 和 [3,3] 。第一个子数组头尾数字的最大公约数为 2 ,第二个子数组头尾数字的最大公约数为 3 。
#include<bits/stdc++.h>
using namespace std;
int n,a[1010],b[1010],ans;
map<int,int> mp;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
mp[a[i]]++;
if(mp[a[i]]==1)
{
ans++;
}
}
cout << ans;
return 0;
}4.集合总和
【问题描述】给定一个n个整数的集合X={x1,x2,...xn}(X中可能包含重复元素)和整数y,找出和等于y的X的子集Y。例如说,如果X={10,30,20,60,40,50},和y=60,则有4种不同的解,他们分别是{10,20,30},{10,50}{20,40},{60}。
【输入形式】输入的第1行包含两个整数n和y,分别表示集合X的长度和目标整数y。接下来1行包含n个整数(整数之间以空格分割),表示X中的n个元素。
【输出形式】输出1行包含1个整数,表示不同的解决方案(不能包含重复的方案数)。
【样例输入】
6 60
10 30 20 60 40 50
【样例输出】
4
#include<bits/stdc++.h>
using namespace std;
int n,y,a[1010],ans;
map<int,int> mp;
bool cmp(int x,int y)
{
if(x>y)
return true;
else
return false;
}
void solve(int k,int summ)
{
if(k>n) return ;
if(summ==y)
{
ans++;
return;
}
else
{
for(int j=k+1;j<=n;j++)
{
if(summ+a[j]<=y)
{
solve(j,summ+a[j]);
}
}
}
return ;
}
int main()
{
cin>>n;
cin>>y;
for(int i=1;i<=n;i++)
{
cin>>a[i];
mp[a[i]]++;
//cout << a[i]<<" ";
}
sort(a+1,a+n+1,cmp);
int flag=0;
for(int i=1;i<=n;i++)
{
if(a[i]>y) continue;
if(mp[a[i]]>=2) flag=1;
solve(i,a[i]);
}
if(flag==1)
{
cout << ans-2;
}
else
cout << ans;
return 0;
}5.批处理作业调度问题
【问题描述】 给定n个作业的集合{J1,J2,…,Jn}。每个作业必须先由机器1处理,然后由机器2处理。作业Ji需要机器j的处理时间为tij(i=1,2,……,n;j=1,2)。对于一个确定的作业调度,设Fji是作业i在机器j上完成处理的时间,则所有作业在机器2上完成处理的时间和
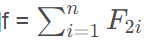
称为该作业调度的完成时间和。
【输入形式】
输入数据有3行;
第一行是作业个数n;
第二行有n个数,是n个作业在机器1上需要的处理时间;
第三行有n个数,是n个作业在机器2上需要的处理时间;
【输出形式】
输出数据有2行;
第一行是三个作业的最佳调度顺序;
第二行是该作业调度的完成时间和;
【样例输入】
3
2 3 2
1 1 3
【样例输出】
1 3 2
18
#include<bits/stdc++.h>
using namespace std;
#define N 100
int n;
int f1=0,f2[N]={0},f=0,a[N][N],best[N],x[N];
int bestf=1e8;
int backpack(int t,int n)
{
if(t>n)
{
for(int i=1;i<=n;i++)
{
best[i]=x[i];
}
bestf=f;
}
for(int i=t;i<=n;i++)
{
f1+=a[1][x[i]];
f2[t] = ((f2[t-1]>f1)?f2[t-1]:f1)+a[2][x[i]];
f+=f2[t];
if(f<bestf)
{
swap(x[i],x[t]);
backpack(t+1,n);
swap(x[t],x[i]);
}
f1-=a[1][x[i]];
f-=f2[t];
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
x[i]=i;
}
for(int i=1;i<=2;i++)
{
for(int j=1;j<=n;j++)
{
cin>>a[i][j];
}
}
backpack(1,n);
for(int i=1;i<=n;i++)
{
cout<<best[i]<<" ";
}
cout<<endl<<bestf<<endl;
return 0;
}