快速排序（Java分治法）

---

---

0、 分治策略

快速排序是对气泡排序的一种改进方法，它是由C.A.R. Hoare于1962年提出的

快速排序的分治策略

• 划分：选定一个记录作为轴值，以轴值为基准将整个序列划分为两个子序列r₁ … r_i-1和r_i+1 … r_n，前一个子序列中记录的值均小于或等于轴值，后一个子序列中记录的值均大于或等于轴值；

• 求解子问题：分别对划分后的每一个子序列递归处理；

• 合并：由于对子序列r₁ … r_i-1和r_i+1 … r_n的排序是就地进行的，所以合并不需要执行任何操作。

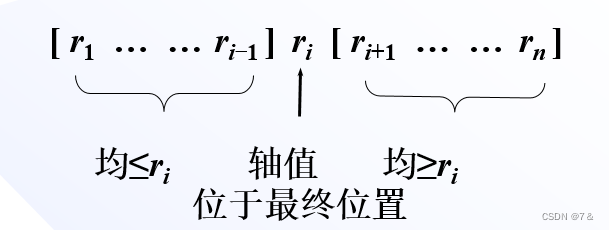
• 合并排序按照记录在序列中的位置对序列进行划分
• 快速排序按照记录的值对序列进行划分

1、思路步骤

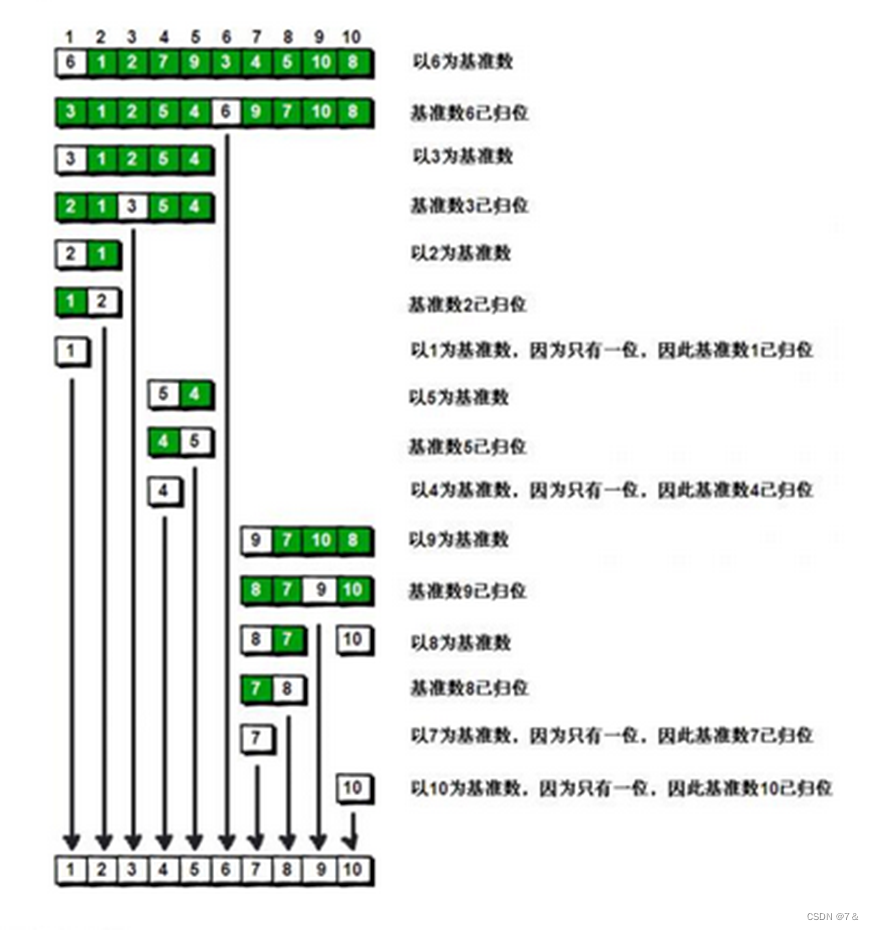
以第一个记录作为轴值，对待排序序列进行划分的过程为：

• 初始化：取第一个记录作为基准，设置两个参数i，j分别用来指示将要与基准记录进行比较的左侧记录位置和右侧记录位置，也就是本次划分的区间；

• 右侧扫描过程：将基准记录与j指向的记录进行比较，如果j指向记录的关键码大，则j前移一个记录位置。重复右侧扫描过程，直到右侧的记录小（即反序），若i＜j，则将基准记录与j指向的记录进行交换；

• 左侧扫描过程：将基准记录与i指向的记录进行比较，如果i指向记录的关键码小，则i后移一个记录位置。重复左侧扫描过程，直到左侧的记录大（即反序），若i＜j，则将基准记录与i指向的记录交换；

• 重复（2）（3）步，直到i与j指向同一位置，即基准记录最终的位置。

2、代码

private static void qSort(int p, int r) {
    if (p<r) {
      int q = partition(p,r); // 以a[p]为基准元素将a[p:r]划分成3段a[p:q-1],a[q]和a[q+1:r]，使得a[p:q-1]中任何元素小于等于a[q]，a[q+1:r]中任何元素大于等于a[q]。下标q在划分过程中确定。
      qSort (p,q-1); //对左半段排序
      qSort (q+1,r); //对右半段排序
      }
 }
 private static int partition (int p, int r) {
    int i = p,  //设置数组第一个下标，这样循环访问从第二个元素开始
        j = r + 1;  //设置下表为长度加1,循环访问从最后一个元素开始
    Comparable x = a[p];
    // 将>= x的元素交换到左边区域
    // 将<= x的元素交换到右边区域
    while (true) {
      while (a[++i].compareTo(x) < 0);
      while (a[--j].compareTo(x) > 0);
      if (i >= j) break;  //I,j游标会合时退出循环
      MyMath.swap(a, i, j);
    } 
    a[p] = a[j];
    a[j] = x;
    return j;  交换位置并返回分割点位置
 }

在快速排序中，记录的比较和交换是从两端向中间进行的，关键字较大的记录一次就能交换到后面单元，关键字较小的记录一次就能交换到前面单元，记录每次移动的距离较大，因而总的比较和移动次数较少。

3、复杂度分析

3.1 最好情况

在最好情况下，每次划分对一个记录定位后，该记录的左侧子序列与右侧子序列的长度相同。在具有n个记录的序列中，一次划分需要对整个待划分序列扫描一遍，则所需时间为O(n)。设T(n)是对n个记录的序列进行排序的时间，每次划分后，正好把待划分区间划分为长度相等的两个子序列，则有：

T(n)≤2 T(n/2)＋n
      ≤2(2T(n/4)＋n/2)＋n＝4T(n/4)＋2n
      ≤4(2T(n/8)＋n/4)＋2n＝8T(n/8)＋3n
      … … … 
      ≤nT(1)＋nlog2n＝O(nlog2n) 

因此，时间复杂度为O(nlog2n)。

注意这个n是指划分所用的时间复杂度而不是合并的时间复杂度

3.2 最坏情况

在最坏情况下，待排序记录序列正序或逆序，每次划分只得到一个比上一次划分少一个记录的子序列（另一个子序列为空）。此时，必须经过n-1次递归调用才能把所有记录定位，而且第i趟划分需要经过n-i次关键码的比较才能找到第i个记录的基准位置，因此，总的比较次数为：

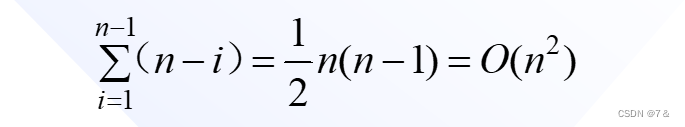
因此，时间复杂度为O(n²)。

3.3 平均情况

我们假设平均情况下，每次分区之后，两个分区的大小比例为 1：k。当 k =9 时，如果用递推公式的方法来求解时间复杂度的话，递推公式就写成 T(n) = T(n/10) + T(9n/10) + n。

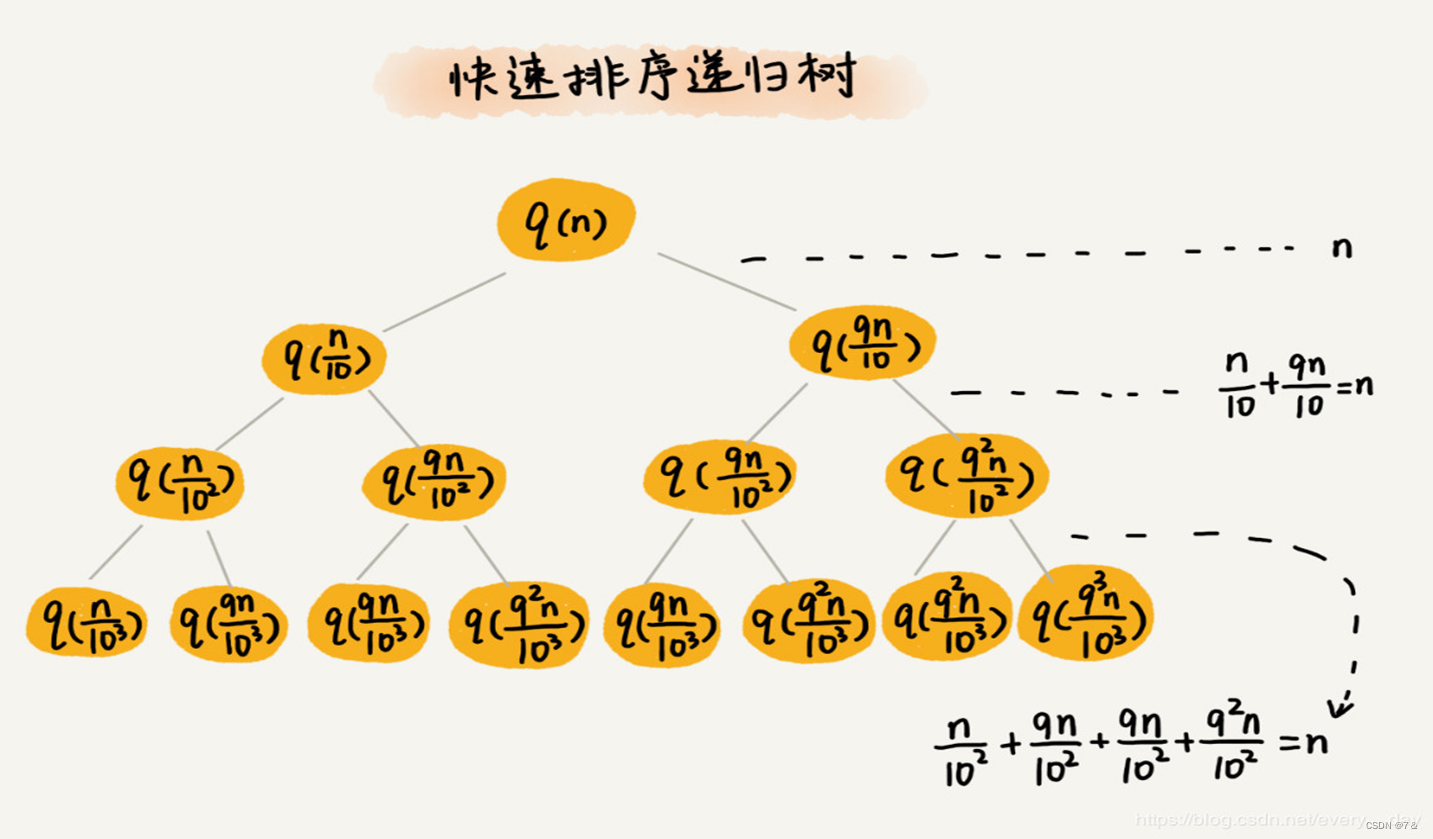
快速排序的过程上，每次分区都要遍历待分区区间的所有数据，所以，每一层分区操作所遍历的数据的个数之和就是n。我们现在只要求出递归的高度h，这个快排过程遍历的个数就是 hn ,也就是说，时间复杂度就是O(hn)。

递归树不是满二叉树。这样一个递归树的高度是多少呢？

快速排序结束的条件就是待排序的小区间，大小为1，也就是说叶子节点的数据规模是1。从根节点n 到叶子节点1，递归树中最短的一个路径是每次都乘以 1/10，最长的路径是每次都乘以9/10。

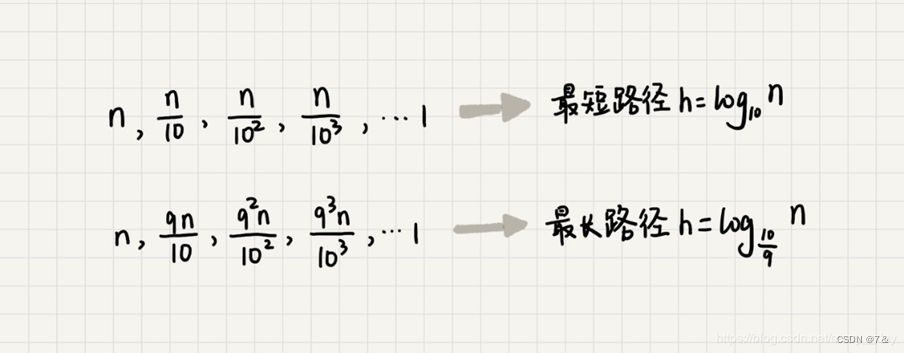
根据复杂度大O表示法，对数复杂度的底数不管是多少，我们统一写成logn，所有当大小比例是1：9时，快速排序的时间复杂度仍然是O(nlogn)。当 k = 99时，算出的时间复杂度也一样。

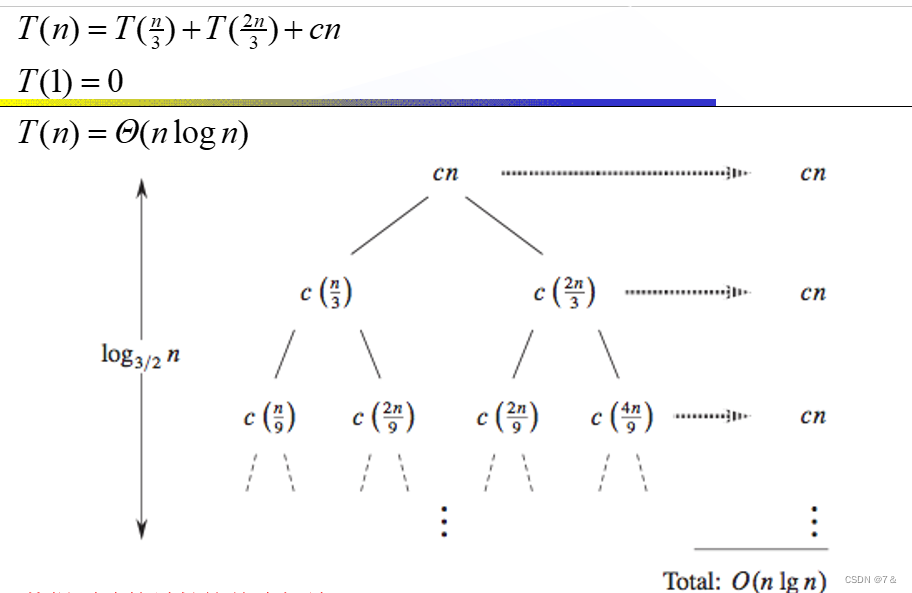
从根到叶的最长简单路径是n–>(2/3)n–>(2/3)^2n–>…–>1。由于当k = log_3/2n时，(2/3)^k*n = 1,因此树高为log_3/2n。

在平均情况下，设基准记录的关键码第k小（1≤k≤n），则有：

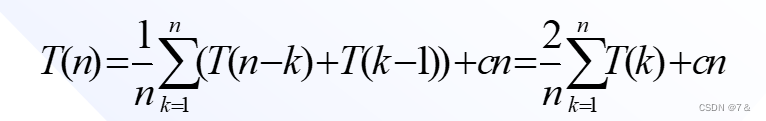
这是快速排序的平均时间性能，可以用归纳法证明，其数量级也为O(nlog2n)。

3.4 性能影响因素

快速排序算法的性能取决于划分的对称性。通过修改算法partition，可以设计出采用随机选择策略的快速排序算法。在快速排序算法的每一步中，当数组还没有被划分时，可以在a[p:r]中随机选出一个元素作为划分基准，这样可以使划分基准的选择是随机的，从而可以期望划分是较对称的。

private static int randomizedPartition (int p, int r) {
    int i = random(p,r);
    MyMath.swap(a, i, p);
    return partition (p, r);
}

• 最坏时间复杂度：O(n2)
• 平均时间复杂度：O(nlogn)
• 辅助空间：O(n)或O(logn)
• 稳定性：不稳定

4、合并排序VS快速排序

快排的前身是归并，归并的最大问题是需要额外的存储空间，并且由于合并过程不确定，致使每个元素在序列中的最终位置上不可预知的。针对这一点，快速排序提出了新的思路：把更多的时间用在“分”上，而把较少的时间用在“治”上。从而解决了额外存储空间的问题，并提升了算法效率

v

如何确定这个基准值呢？

• 随机
  在所要排序的数组中，随机选取一个数来作为基准值，需要将其交换到最边上。

• 直接取最边上的值（任选左右）。

• 三数取中法

在[left, left +(right -left)/2, righ ] 中，通过判断，选取其中大小为 中 的元素。

5、参考

• 算法设计与分析（第4版）

结束！