🐒个人主页

🏅算法思维框架

📖前言：

本篇博客主要以介绍十大排序算法中的计数排序和桶排序以及基数排序，有详细的图解、动画演示、良好的代码注释，帮助加深对这些算法的理解，进行查漏补缺~

🎀计数排序 时间复杂度O(n+k)

当输入的元素是 n 个 0 到 k 之间的整数时，它的运行时间是 O(n + k)。计数排序不是比较排序，排序的速度快于任何比较排序算法。
计数排序需要拿一个辅助数组来统计待排序数组中元素的数量，再将统计的结果从小到大回填到待排序数组中。

🎇1. 算法步骤思想

（1）找出待排序的数组中最大的元素
（2）统计数组中每个值为i的元素出现的次数，存入数组C的第i项
（3）对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）
（4）反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1

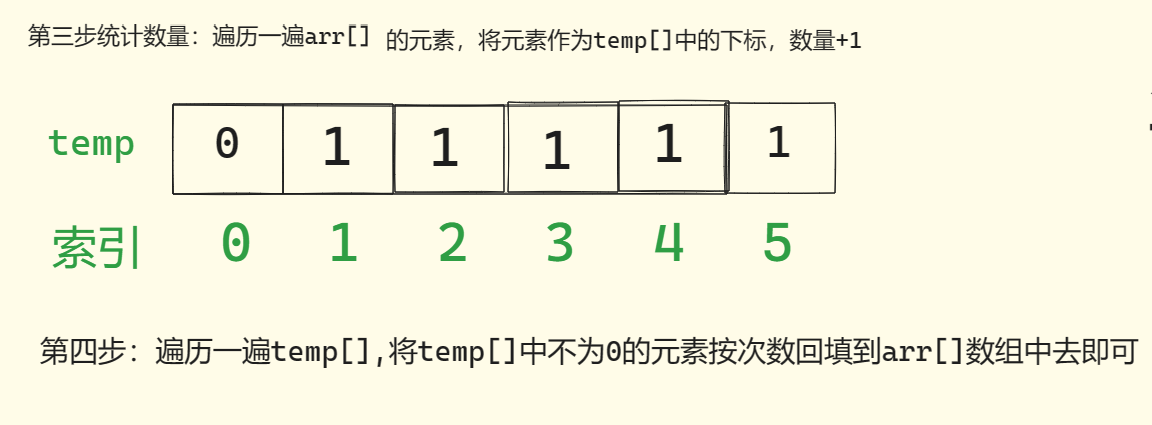
🎇2.动画实现

🎇 3.代码实现

    //使用前提：arr【】中的元素介于【0,k】 k值不要太大，
    // 思路启示：如果元素值介于【-1000，1000】,可以创建一个【0,2000】的辅助数组下标0 对应 -1000平移一下，来统计。回填时再-1000就行了
    public void sort(int[] arr){
        if(arr==null||arr.length<2){
            return;
        }
        //利用哈希数组temp[]进行排序,将arr[]中的值作为temp[]的键进行存储，统计其出现的数量
        int maxVal=arr[0];
        for (int i = 1; i <arr.length ; i++) {//获取arr[]数组中的最大值
            maxVal=maxVal<arr[i]?arr[i]:maxVal;
        }
        int[] temp=new int[maxVal+1];//哈希数组--统计数量
        for (int i : arr) {
            temp[i]+=1;
        }
        //进行排序
        int index=0;
        for (int i = 0; i <temp.length ; i++) {
            int count=temp[i];
            if(count!=0){
                while (count>0){
                    arr[index++]=i;
                    count--;
                }
            }
        }
    }

🎀桶排序

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效，我们需要做到这两点：

• 在额外空间充足的情况下，尽量增大桶的数量
• 使用的映射函数能够将输入的 N个数据均匀的分配到 K 个桶中

同时，对于桶中元素的排序，选择何种比较排序算法对于性能的影响至关重要。

1. 什么时候最快？ 当输入的数据可以均匀的分配到每一个桶中。
2. 什么时候最慢？ 当输入的数据被分配到了同一个桶中。

🎇1. 算法步骤思想

确定桶的个数，以及哪个元素放到哪一个桶里：
假设对介于[0,100)的元素进行排序，要分成十个桶，
【0-9】【10-19】【20-29】…【90-99】
对每一个桶单独排序，因为每个桶里面数据很少，所以排序很快

🎇2、示意图

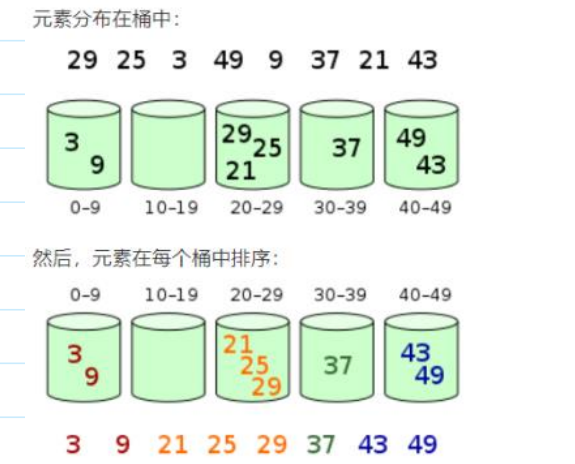
🪀桶排序详解

🎇3.代码实现

 public void sort(int[] arr){
        if(arr==null||arr.length<2){
            return;
        }
        //思路：假设对介于[0,100)的元素进行排序，要分成十个桶，【0~9】【10~19】【20~29】...【90~99】
        List<Integer>[] bucket=new ArrayList[10];
        for (int i = 0; i <bucket.length ; i++) {
            bucket[i]=new ArrayList<>();//生成桶
        }
        //将元素放入桶内
        Arrays.stream(arr).boxed().forEach(item->{
            bucket[item/10].add(item);
        });
        //对每个桶进行排序，由于每个桶的元素很少，故排序很快，这里可以使用任意的排序算法，我先使用内置的库函数来代替任意排序算法了
        int index=0;//将元素存入arr的下标
        for (int i = 0; i <bucket.length ; i++) {

                Collections.sort(bucket[i]);//对每个桶进行排序
                //放入arr数组中
                for (int item : bucket[i]) {//拿到这个桶
                    arr[index++]=item;
                }
        }
    }

🎀基数排序 （RadixSort）

原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。基数排序的方式可以采用 LSD（Least significant digital）或MSD（Most significant digital），LSD的排序方式由键值的最右边开始，而MSD则相反，由键值的最左边开始。
(不常用)MSD：先从高位开始进行排序，在每个关键字上，可采用计数排序
(常用)LSD：先从低位开始进行排序，在每个关键字上，可采用桶排序

🏨 基数排序 vs 计数排序 vs 桶排序

这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：

• 基数排序：根据键值的每位数字来分配桶；
• 计数排序：每个桶只存储单一键值；
• 桶排序：每个桶存储一定范围的数值；

🎇1. LSD算法步骤思想（按低位到高位排序）

分步图示说明：设有数组 array = {53, 3, 542, 748, 14, 214, 154, 63, 616}，对其进行基数排序：

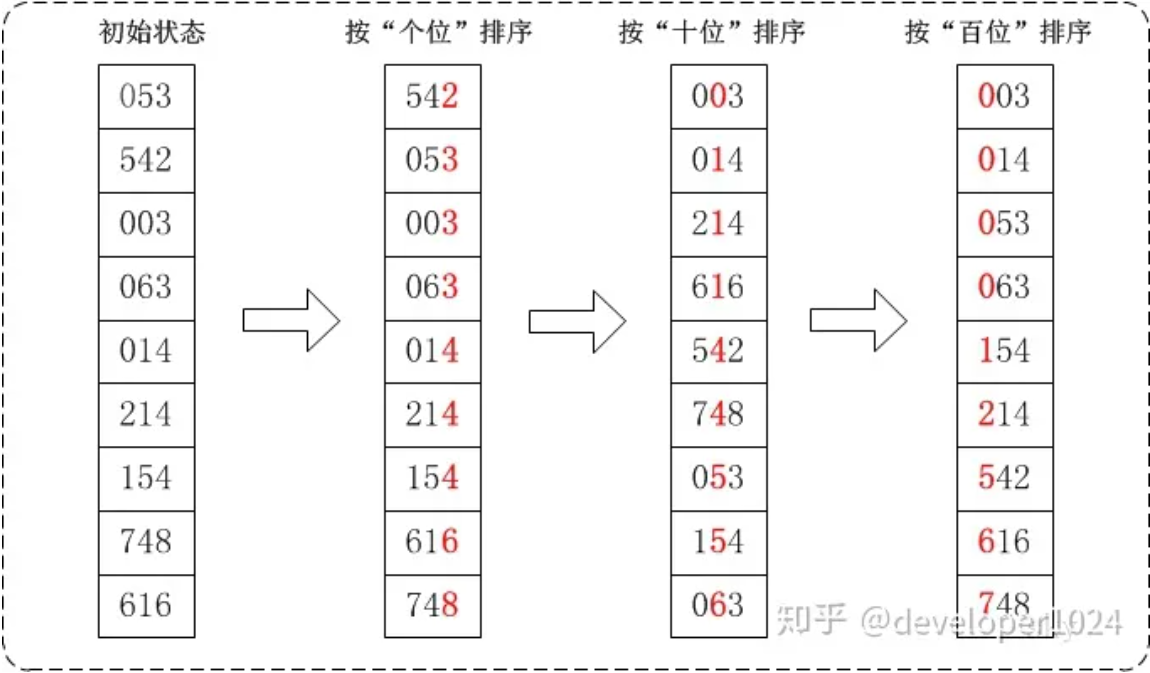
在上图中，首先将所有待比较数字统一为统一位数长度，接着从最低位开始，依次进行排序。

按照个位数进行排序。将结果回填到array[]中
按照十位数进行排序。将结果回填到array[]中
按照百位数进行排序。将结果回填到array[]中
排序后，数列就变成了一个有序序列。

🎇 3.代码实现

   //思路：基数排序是在桶排序的基础上进行了优化：
    // LSD从低位到高位进行的排序：
    // 原理是先找到数组最大值的位数，分成10个桶，先按照个位数进行桶排序，再进行回填，再按十位数进行桶排序，进行回填...直到按最高位进行排序，进行回填

    //【基于LSD排序方式实现的基数排序】
    public void sort(int[] arr){
        if(arr==null||arr.length<2){
            return;
        }
       //思路：先获取数组中最大值的个数
        int max=0;
        for (int i : arr) {
            //计算值的位数
            int digt=(i+"").length();
            max=max<digt?digt:max;
        }
        int dev=1;//获取个位，十位，百位...的上的数字
        for (int i = 0; i <max ; i++) {
            //进行桶排序
            List<Integer>[] bucket=new ArrayList[10];
            for (int j = 0; j < bucket.length; j++) {
                bucket[j]=new ArrayList<>();//创建桶
            }
            //放入桶进行排序
            for (int item : arr) {
                bucket[item/dev%10].add(item);
            }
            //进行排序+回填
            int index=0;
            for (int j = 0; j <bucket.length ; j++) {
                Collections.sort(bucket[j]);
                for (int item : bucket[j]) {
                    arr[index++]=item;
                }
            }
            dev*=10;
        }
    }