目录
树的概念
关于树的概念
二叉树
概念
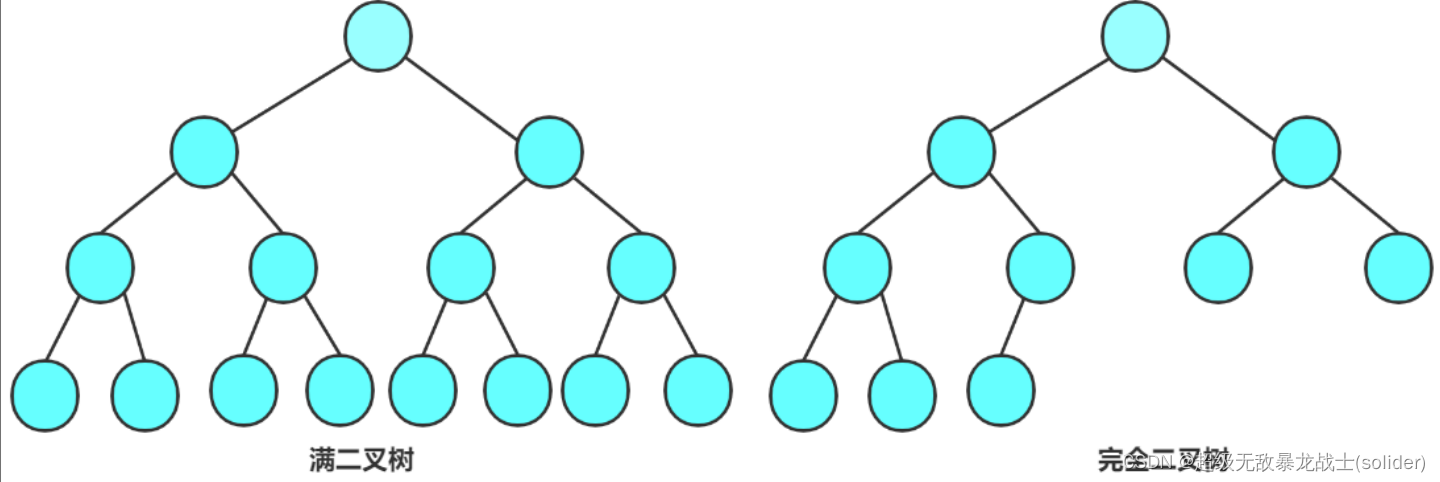
两种特殊的二叉树
满二叉树
完全二叉树
二叉树的性质
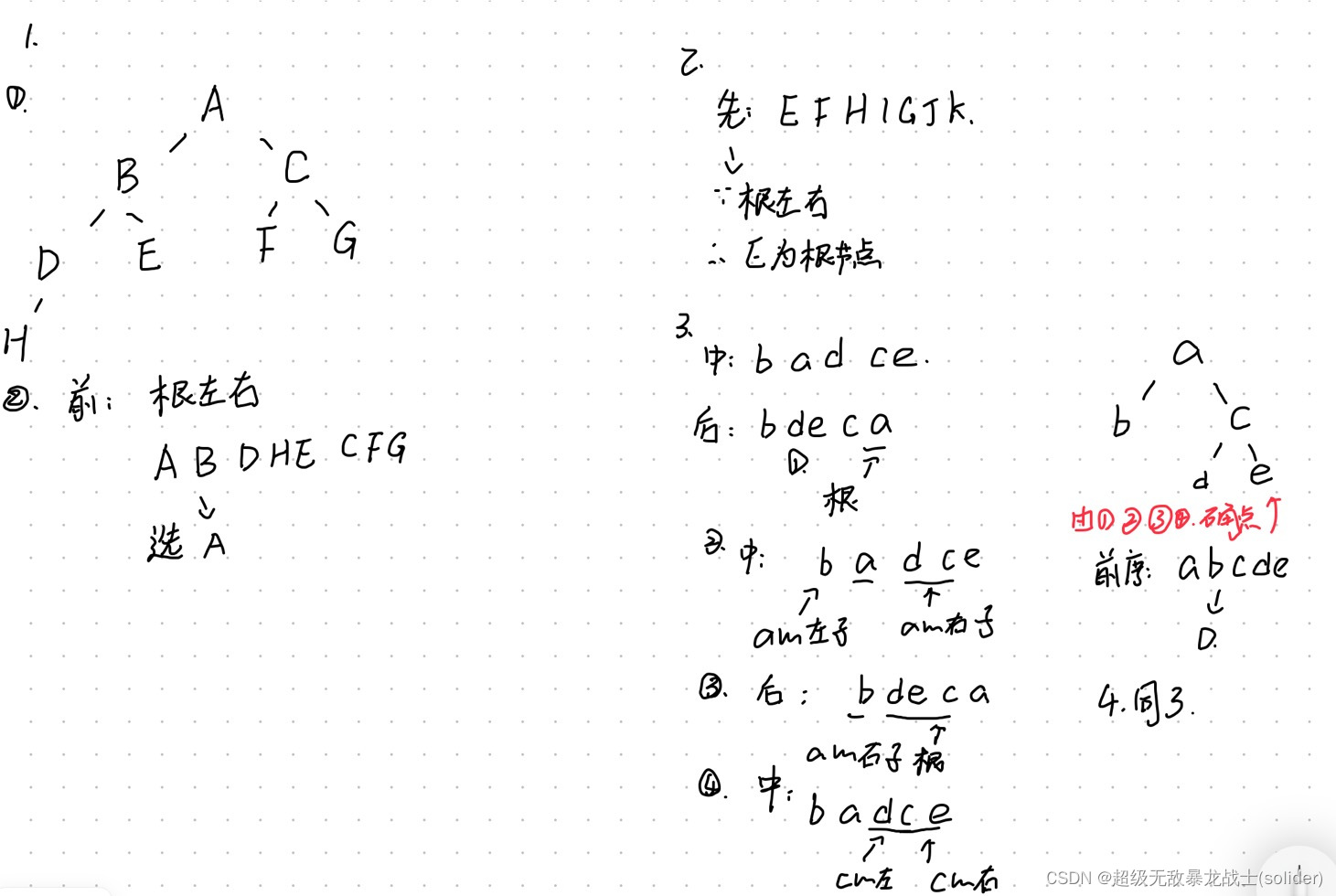
巩固性质的习题
简单的创建二叉树
二叉树的遍历
递归实现二叉树的前中后后序遍历
二叉树的基本操作
获取树中节点个数
获取叶子结点个数
子问题思路-获取叶子结点个数
获取第K层结点个数
获取二叉树的高度
判断值为key的元素是否存在
树的概念
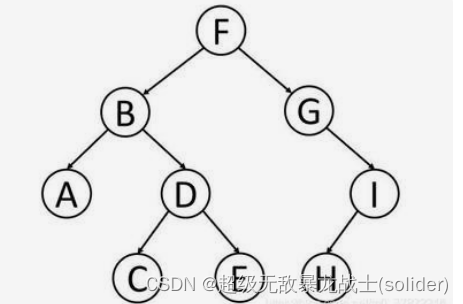
关于树的概念
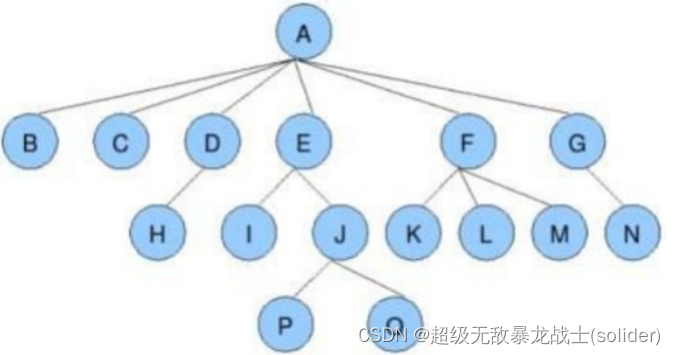
二叉树
概念
两种特殊的二叉树
满二叉树
完全二叉树
二叉树的性质
1.若规定根结点个数为1,则一颗非空二叉树的第i层上最多有2的(i-1)次方个结点。(i>0)
2.若规定只有根结点的二叉树深度为1,则深度为K的二叉树的最大结点数为2的k次方-1(k>=0)
3.对如何一颗二叉树,如果其叶结点个数为N0(度为0的结点称为叶结点),度为2的非叶结点个数为N2,则N0 = N2 + 1
4.具有N个结点的完全二叉树的深度为 log2(N+1)上取整
5.对于具有N个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有结点从0开始编号,则对于序号为 i 的结点有:
若 i > 0 ,双亲序号:(i-1)/ 2 ;i = 0,i 为根结点编号,无双亲结点
若2i + 1 < n,左孩子序号:2i + 1,否则无左孩子
若2i + 1 < n,右孩子序号:2i + 1,否则无右孩子
【数据结构】之二叉树的5个性质_二叉树的性质-CSDN博客
巩固性质的习题
A 不存在这样的二叉树B 200C 198D 199
A nB n+1C n-1D n/2

A 383B 384C 385D 386
A 11B 10C 8D 12
解析:log2(531)上取整 。2的10次方=1024>531 ,2的9次方=512<531 选B
二叉树的存储
二叉树的存储结构分为:顺序存储和类似与链表的存储
孩子表示法:
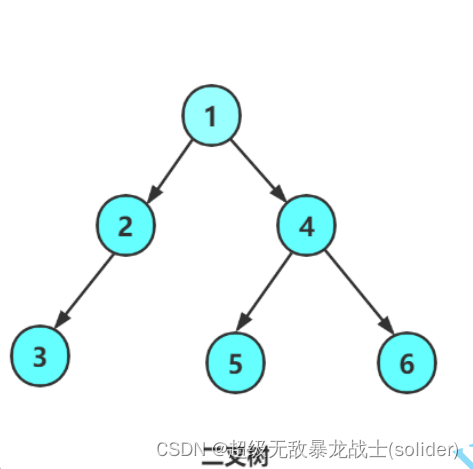
简单的创建二叉树
public class BinaryTree {
public static class BTNode{
BTNode left;
BTNode right;
int val;
BTNode(int val) {
this.val = val;
}
}
private BTNode root;
public void createBinaryTree() {
BTNode node1 = new BTNode(1);
BTNode node2 = new BTNode(2);
BTNode node3 = new BTNode(3);
BTNode node4 = new BTNode(4);
BTNode node5 = new BTNode(5);
BTNode node6 = new BTNode(6);
root = node1;
node1.left = node2;
node2.left = node3;
node1.right = node4;
node4.left = node5;
node5.right = node6;
}
}
二叉树的遍历
A: ABDHECFGB: ABCDEFGHC: HDBEAFCGD: HDEBFGCA
A: E B: F C: G D: H
A: adbce B: decab C: debac D: abcde
A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF
递归实现二叉树的前中后后序遍历
/*
递归遍历:
*/
//前序遍历
public void preOrder(BTNode root) {
if(root==null) {
return;
}
//前序:根左有
System.out.println(root.val+" ");
preOrder(root.left);
preOrder(root.right);
}
//中序遍历
public void inOrder(BTNode root) {
if(root == null) {
return;
}
inOrder(root.right);
System.out.println(root.val+ " ");
inOrder(root.left);
}
//后序遍历
public void postOrder(BTNode root) {
if(root==null) {
return;
}
postOrder(root.left);
postOrder(root.right);
System.out.println(root.val+" ");
}二叉树的基本操作
获取树中节点个数
//一.获取结点个数
public int size = 0;
//1.遍历思路
public int nodeSize(BTNode root) {
if(root==null){
return 0 ;
}
//根结点++
size++;
nodeSize(root.left);
nodeSize(root.right);
return size;
}方法二:当前root结点总数 = 左树子树结点个数+右数结点个数+1
//2.子问题思路,要算当前root结点总数:
// 左树子树结点个数+右数结点个数+1
public int nodeSize2(BTNode root) {
if(root==null) {
return 0;
}
return nodeSize2(root.left) +
nodeSize2(root.right) + 1;
}获取叶子结点个数
获取叶子结点(度为0的结点)的个数 1.遍历思路 一个结点的左边右边都为空,证明为叶子结点
//二.获取叶子结点(度为0的结点)的个数
//1.遍历思路
//一个结点的左边右边都为空,证明为叶子结点
public int leafSize = 0;
public int getLeafSize(BTNode root) {
if(root==null) {
return 0 ;
}
if(root.right==null&&root.left==null) {
leafSize++;
}
getLeafSize(root.left);
getLeafSize(root.right);
return leafSize;
}子问题思路-获取叶子结点个数
当前二叉树叶子结点个数
= 根结点左边的叶子结点个数 + 根结点右边的叶子个数
//2.子问题思路,要算当前二叉树叶子结点个数
// = 根结点左边的叶子结点个数 + 根结点右边的叶子个数
public int getLeafSize2(BTNode root) {
if(root==null) {
return 0;
}
if(root.left == null && root.right==null) {
return 1;
}
return getLeafSize2(root.left) +
getLeafSize2(root.right);
}获取第K层结点个数
root这颗树的第K层 = root.left 第 K-1 层 +
root.right 的第 K-1层
//三.获取 第K层 结点个数
//子问题:
// root这颗树的第K层 = root.left 第 K-1 层 +
// root.right 的第 K-1层
public int getKLeveNodeCount(BTNode root,int k) {
if(root == null) {
return 0;
}
if(k==1) {
return 1;
}
return getKLeveNodeCount(root.left,k-1) +
getKLeveNodeCount(root.right,k-1);
}获取二叉树的高度
高度 = (root 左树的高度 root 右树的高度 )max + 1
//四.获取二叉树的高度
//高度 = (root 左树的高度 root 右树的高度 )max
// + 1
public int height;
public int getHeight(BTNode root) {
if(root == null) {
return 0;
}
int leftHeight = getHeight(root.left);
int rightHeight = getHeight(root.right);
return (leftHeight > rightHeight ? leftHeight+1 : rightHeight+1);
}判断值为key的元素是否存在
//五.判断K是否在二叉树里
//前序遍历的方式进行二叉树的遍历
public boolean find(BTNode root,int key) {
if(root==null) {
return false;
}
//判断根节点
if(root.val==key) {
return true;
}
//根节点左边
boolean leftVal = find(root.left,key);
if(leftVal==true) {
return true;
}
//根结点右边
boolean rightVal = find(root.right,key);
if(rightVal==true) {
return true;
}
return false;
}