文章目录
- 5.1 树的基本概念
- 5.1.1 树的定义
- 5.1.2 森林的定义
- 5.1.3 树的术语
- 5.2 二叉树
- 5.3 树
- 5.3.1 树的存储结构
- 1. 理论基础
- 2. 典型实例
- 3. Father链接结构
- 4. 儿子链表链接结构
- 5. 左儿子右兄弟链接结构
- 5.3.2 获取结点的算法
- 5.3.3 树和森林的遍历
- 1. 先根遍历(递归、非递归)
- 2. 后根遍历(递归)
- a.理论
- b. ADL算法PostOrder
- c. 代码实现
- 3. 后根遍历(非递归)
- a. ADL算法NPO
- b. NPO算法解析
- c. 代码实现
- 3. 森林的遍历
- 4. 代码整合
5.1 树的基本概念
5.1.1 树的定义
- 一棵树是结点的有限集合T:
- 若T非空,则:
- 有一个特别标出的结点,称作该树的根,记为root(T);
- 其余结点分成若干个不相交的非空集合T1, T2, …, Tm (m>0),其中T1, T2, …, Tm又都是树,称作root(T)的子树。
- T 空时为空树,记作root(T)=NULL。
- 若T非空,则:
5.1.2 森林的定义
一个森林是0棵或多棵不相交(非空)树的集合,通常是一个有序的集合。换句话说,森林由多个树组成,这些树之间没有交集,且可以按照一定的次序排列。在森林中,每棵树都是独立的,具有根节点和子树,树与树之间没有直接的连接关系。
森林是树的扩展概念,它是由多个树组成的集合。在计算机科学中,森林也被广泛应用于数据结构和算法设计中,特别是在图论和网络分析等领域。
5.1.3 树的术语
- 父亲(parent)、儿子(child)、兄弟(sibling)、后裔(descendant)、祖先(ancestor)
- 度(degree)、叶子节点(leaf node)、分支节点(internal node)
- 结点的层数
- 路径、路径长度、结点的深度、树的深度
参照前文:【数据结构】树与二叉树(一):树(森林)的基本概念:父亲、儿子、兄弟、后裔、祖先、度、叶子结点、分支结点、结点的层数、路径、路径长度、结点的深度、树的深度
5.2 二叉树
5.3 树
5.3.1 树的存储结构
1. 理论基础
2. 典型实例
3. Father链接结构
4. 儿子链表链接结构
【数据结构】树与二叉树(十八):树的存储结构——Father链接结构、儿子链表链接结构
5. 左儿子右兄弟链接结构
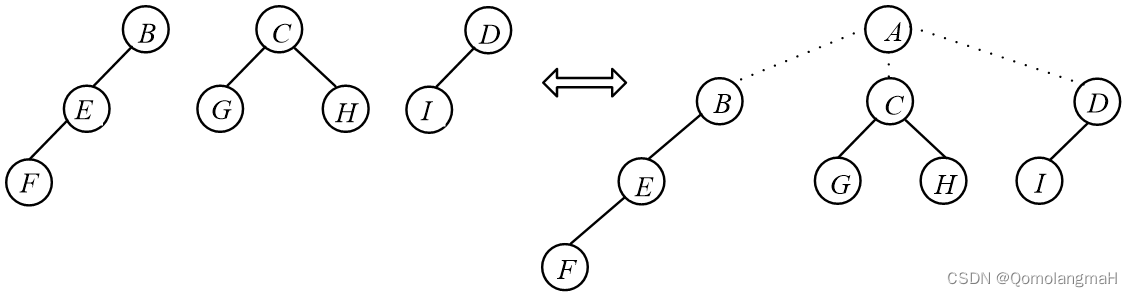
【数据结构】树与二叉树(十九):树的存储结构——左儿子右兄弟链接结构(树、森林与二叉树的转化)
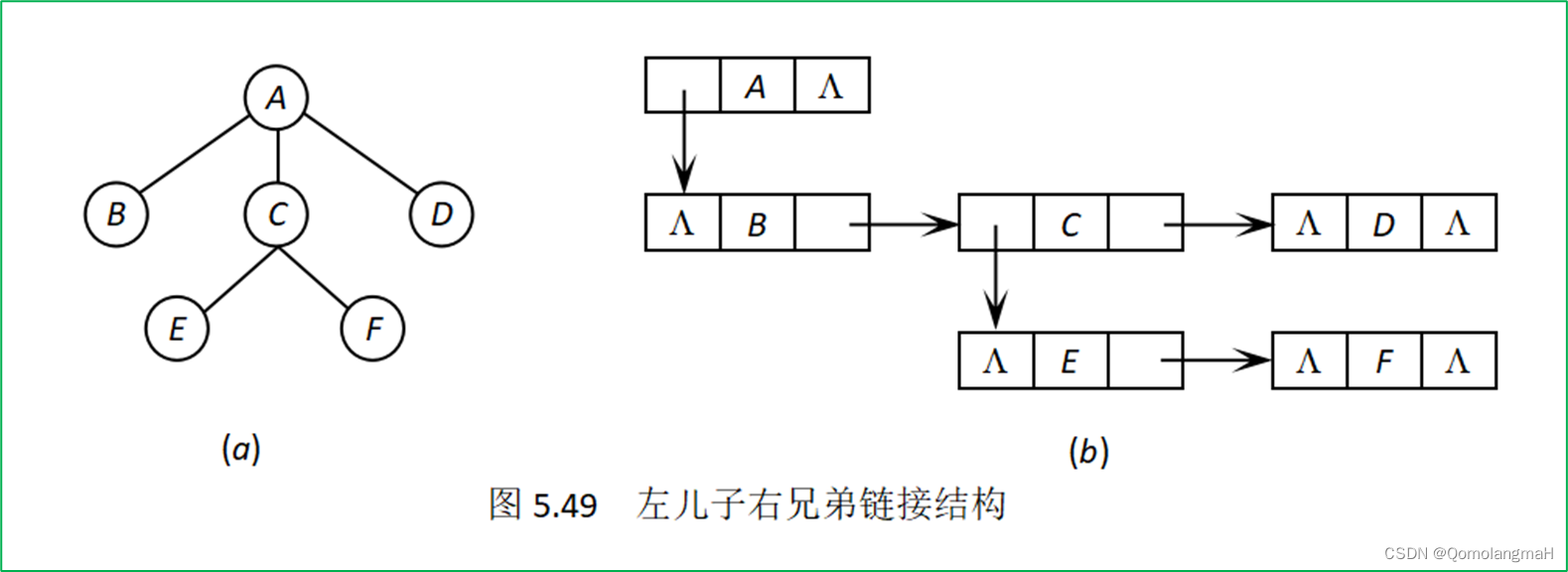
左儿子右兄弟链接结构通过使用每个节点的三个域(FirstChild、Data、NextBrother)来构建一棵树,同时使得树具有二叉树的性质。具体来说,每个节点包含以下信息:
- FirstChild: 存放指向该节点的大儿子(最左边的子节点)的指针。这个指针使得我们可以迅速找到一个节点的第一个子节点。
- Data: 存放节点的数据。
- NextBrother: 存放指向该节点的大兄弟(同一层中右边的兄弟节点)的指针。这个指针使得我们可以在同一层中迅速找到节点的下一个兄弟节点。
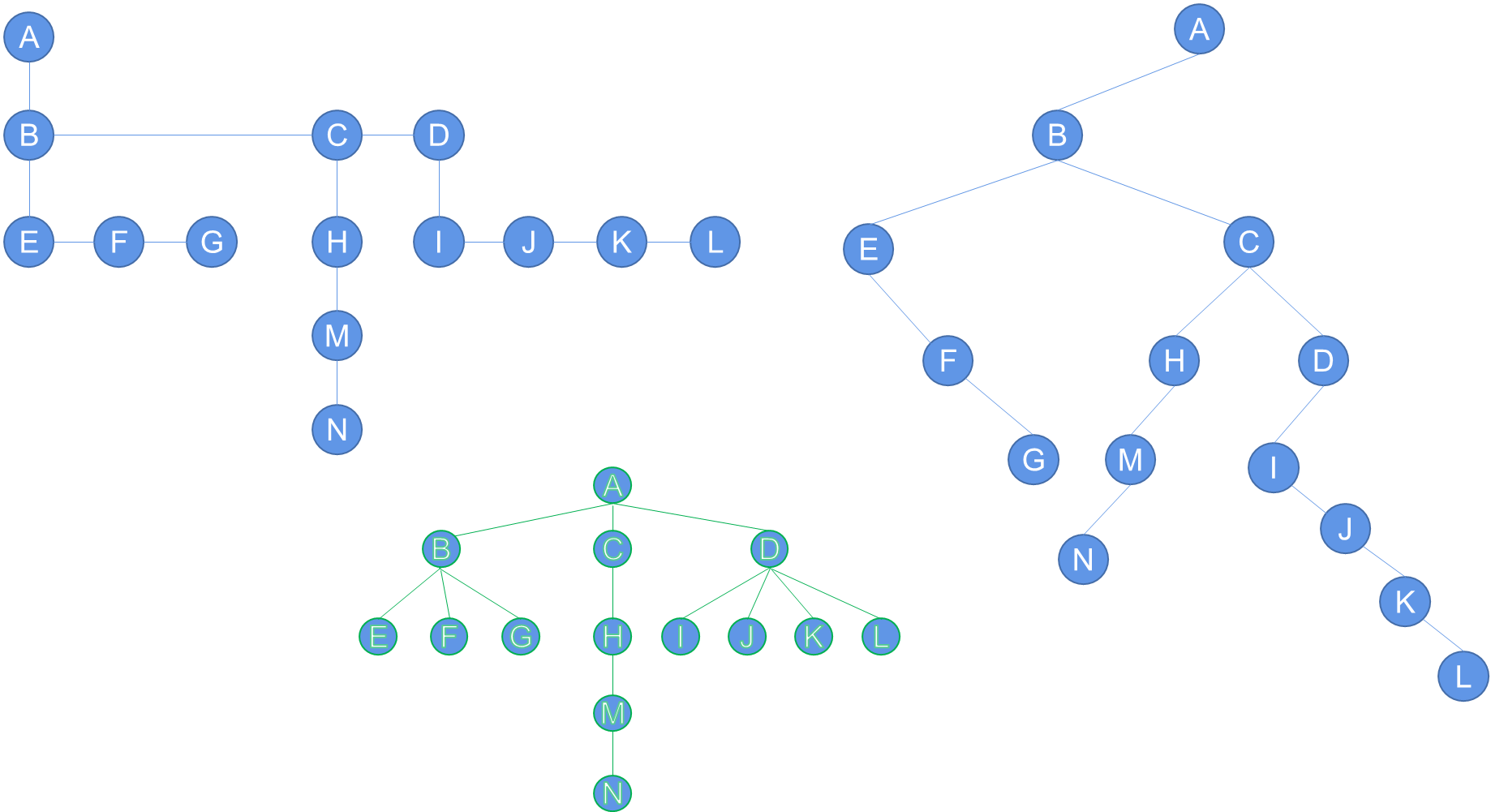
通过这样的结构,整棵树可以用左儿子右兄弟链接结构表示成一棵二叉树。这种表示方式有时候被用于一些特殊的树结构,例如二叉树、二叉树的森林等。这种结构的优点之一是它更紧凑地表示树,而不需要额外的指针来表示兄弟关系。
A
/|\
B C D
/ \
E F
A
|
B -- C -- D
|
E -- F
即:
A
/
B
\
C
/ \
E D
\
F
5.3.2 获取结点的算法
【数据结构】树与二叉树(二十):树获取大儿子、大兄弟结点的算法(GFC、GNB)
5.3.3 树和森林的遍历
【数据结构】树与二叉树(七):二叉树的遍历(先序、中序、后序及其C语言实现)
1. 先根遍历(递归、非递归)
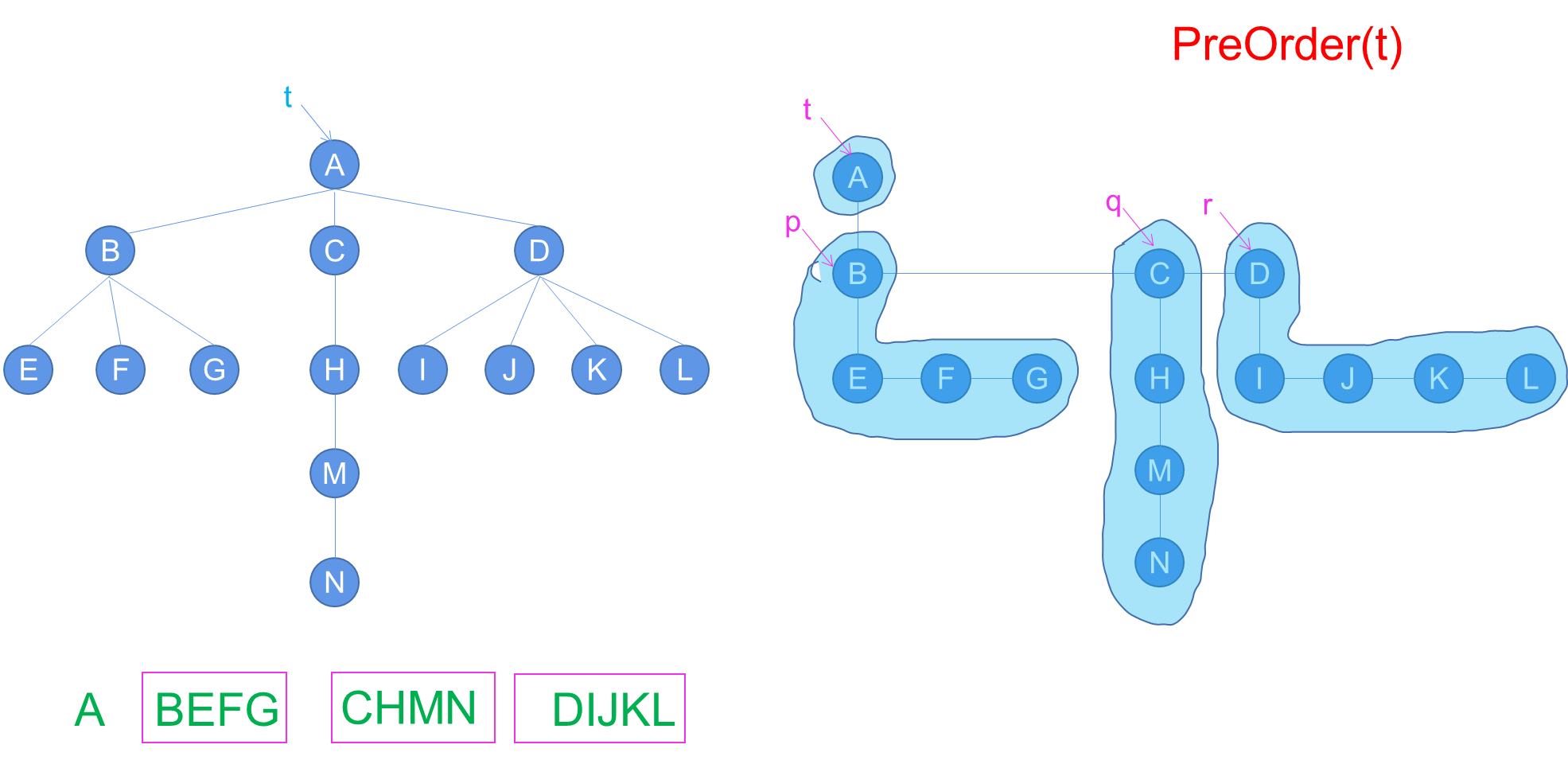
【数据结构】树与二叉树(廿一):树和森林的遍历——先根遍历(递归算法PreOrder、非递归算法NPO)
2. 后根遍历(递归)
a.理论
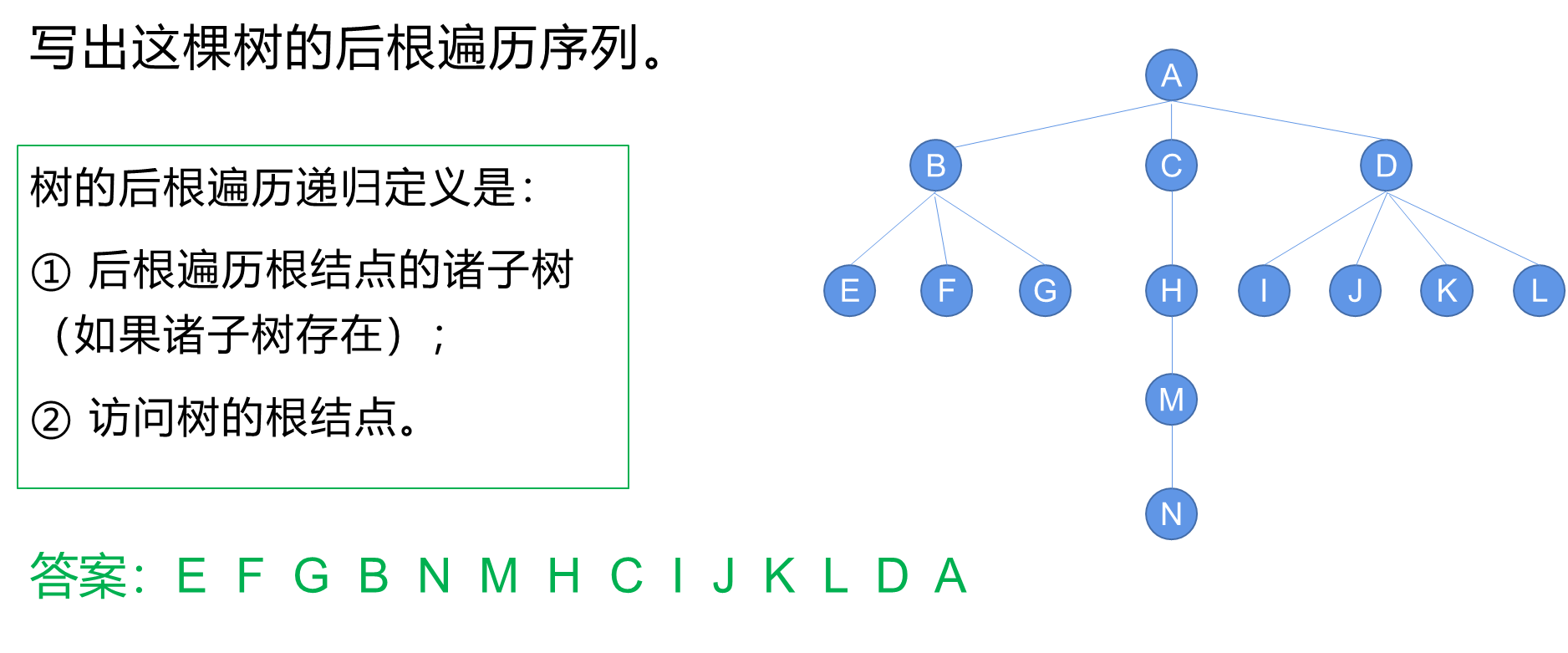
b. ADL算法PostOrder

-
基本条件检查:
IF t=NULL THEN RETURN.:如果树的根节点t为空,直接返回,递归的出口条件。
-
递归调用子树的后根遍历:
PostOrder(t.child).:递归调用后根遍历算法,对当前节点t的第一个孩子进行遍历。
-
迭代调用右兄弟节点的后根遍历:
WHILE child≠∧ DO:使用WHILE循环,判断当前节点的第一个孩子是否存在(child≠∧)。PostOrder(child).:递归调用先根遍历算法,对当前节点child进行遍历。GNB(child.child).:调用算法GNB获取当前节点child的下一个兄弟节点,然后继续遍历。
-
打印根节点数据:
PRINT(Data(t)).:打印当前树节点t的数据。
通过递归地调用后根遍历算法,依次访问树的根节点、根节点的孩子节点、孩子节点的兄弟节点……以此类推,完成对整个树的后根遍历。
c. 代码实现
void PostOrder(TreeNode* t) {
if (t == NULL) {
return;
}
// 递归调用子树的后根遍历
TreeNode* child = getFirstChild(t);
while (child != NULL) {
PostOrder(child);
// 迭代调用右兄弟节点的后根遍历
child = getNextBrother(child);
}
// 打印当前树节点的数据
printf("%c ", t->data);
}
3. 后根遍历(非递归)
a. ADL算法NPO
b. NPO算法解析
暂时仅提供c语言代码,ADL语言及代码解析,有缘再见……
c. 代码实现
// 后根遍历的非递归算法
void NorecPostOrder(TreeNode* root) {
if (root == NULL) {
return;
}
TreeNode* stack1[100];
TreeNode* stack2[100];
int top1 = -1;
int top2 = -1;
TreeNode* p = root;
stack1[++top1] = p;
while (top1 != -1) {
p = stack1[top1--];
stack2[++top2] = p;
TreeNode* child = getFirstChild(p);
while (child != NULL) {
stack1[++top1] = child;
child = getNextBrother(child);
}
}
while (top2 != -1) {
printf("%c ", stack2[top2--]->data);
}
}
-
参数:
root: 树的根节点。
-
局部变量:
stack[100]: 用于模拟栈的数组,存储待访问的节点。
3. 森林的遍历

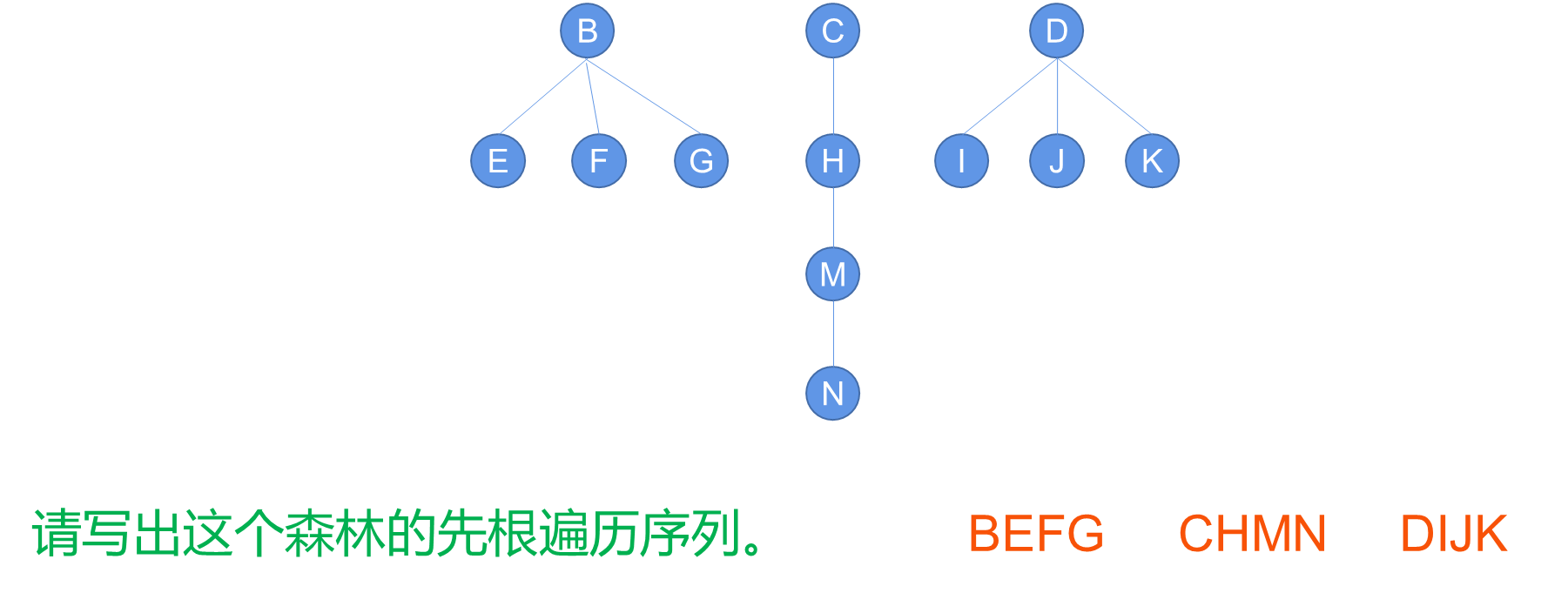
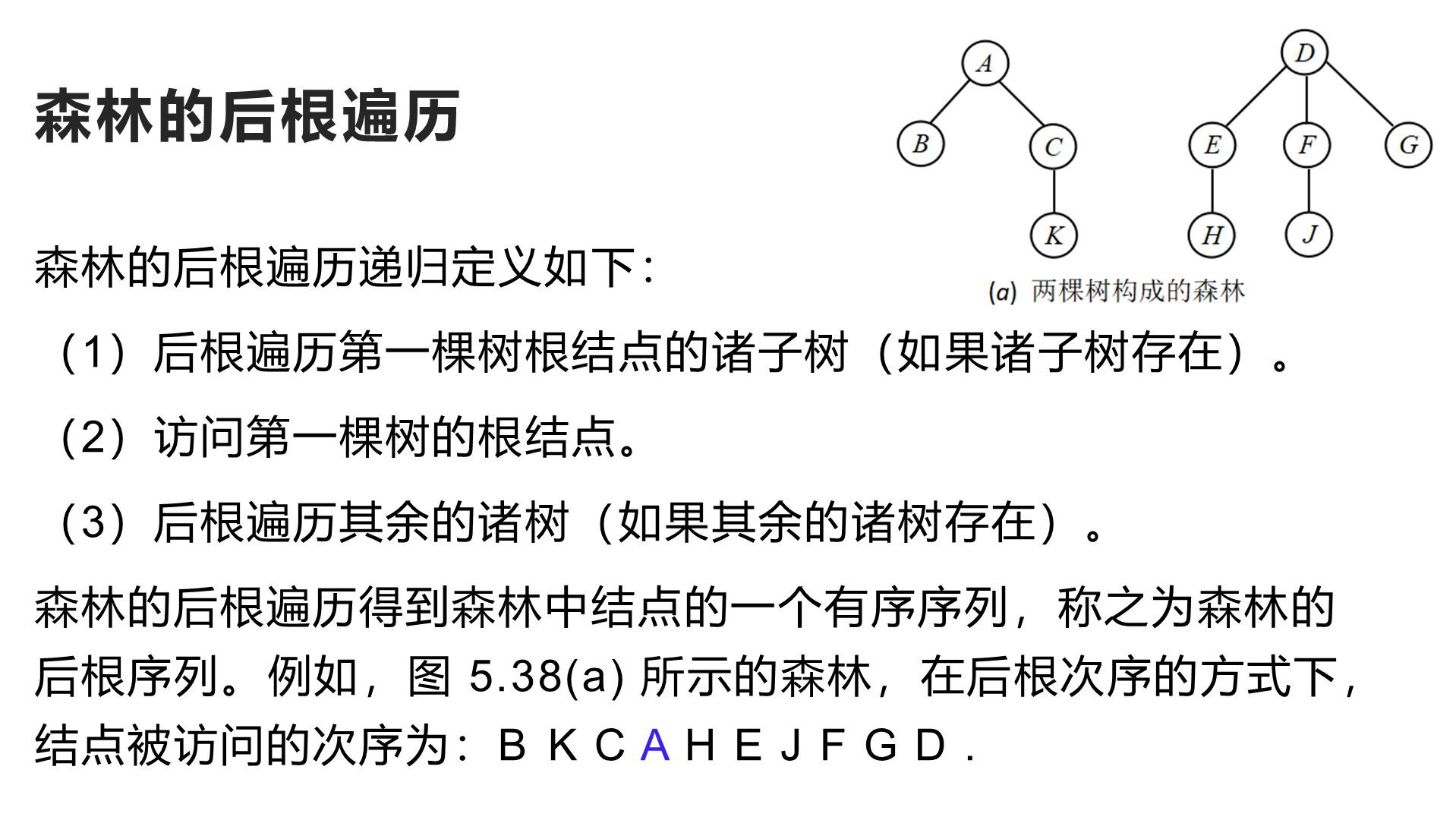
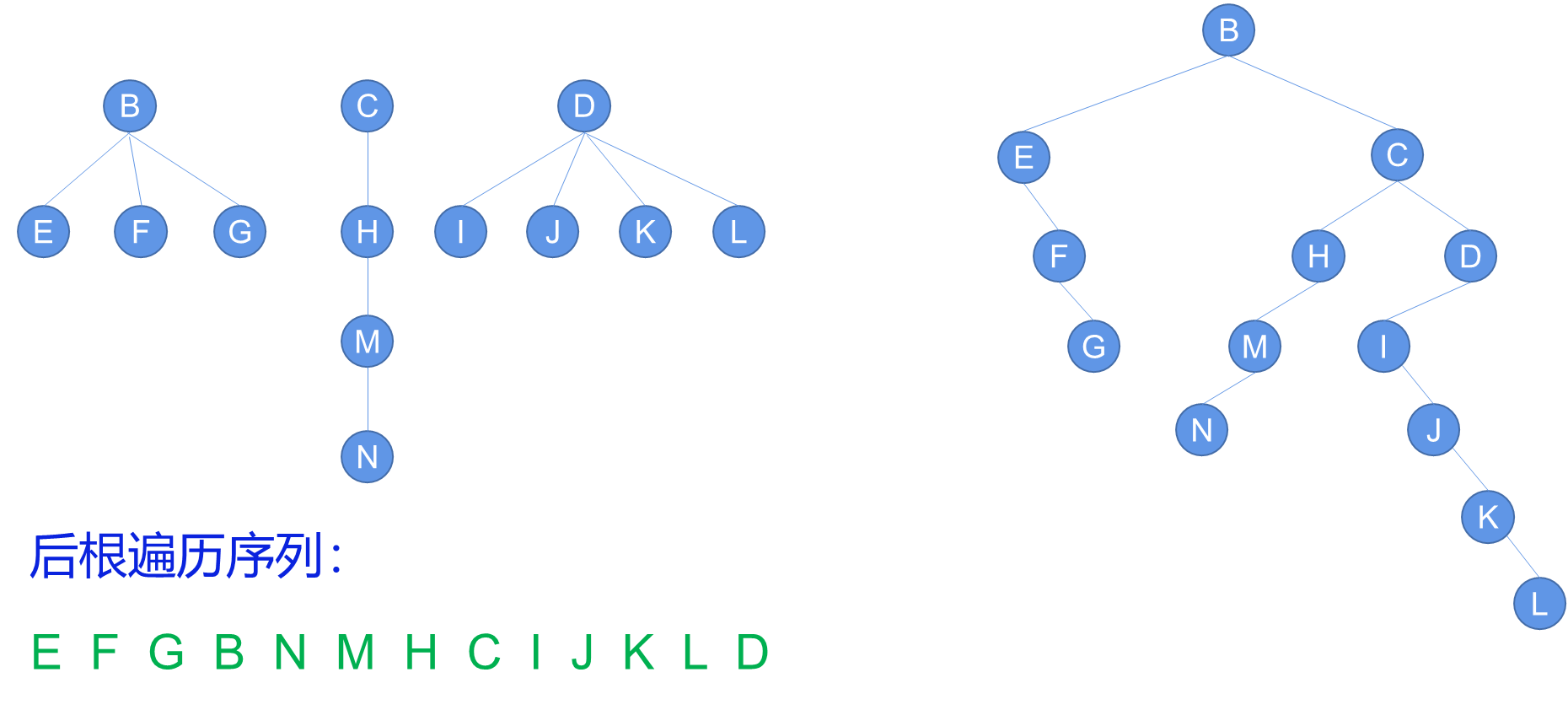
4. 代码整合
#include <stdio.h>
#include <stdlib.h>
// 定义树节点
typedef struct TreeNode {
char data;
struct TreeNode* firstChild;
struct TreeNode* nextBrother;
} TreeNode;
// 创建树节点
TreeNode* createNode(char data) {
TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));
if (newNode != NULL) {
newNode->data = data;
newNode->firstChild = NULL;
newNode->nextBrother = NULL;
}
return newNode;
}
// 释放树节点及其子树
void freeTree(TreeNode* root) {
if (root != NULL) {
freeTree(root->firstChild);
freeTree(root->nextBrother);
free(root);
}
}
// 算法GFC:获取大儿子结点
TreeNode* getFirstChild(TreeNode* p) {
if (p != NULL && p->firstChild != NULL) {
return p->firstChild;
}
return NULL;
}
// 算法GNB:获取下一个兄弟结点
TreeNode* getNextBrother(TreeNode* p) {
if (p != NULL && p->nextBrother != NULL) {
return p->nextBrother;
}
return NULL;
}
/* 使用已知的getFirstChild和getNextBrother函数实现后根遍历以t为根指针的树。*/
void PostOrder(TreeNode* t) {
if (t == NULL) {
return;
}
// 递归调用子树的后根遍历
TreeNode* child = getFirstChild(t);
while (child != NULL) {
PostOrder(child);
// 迭代调用右兄弟节点的后根遍历
child = getNextBrother(child);
}
// 打印当前树节点的数据
printf("%c ", t->data);
}
// 后根遍历的非递归算法
void NorecPostOrder(TreeNode* root) {
if (root == NULL) {
return;
}
TreeNode* stack1[100];
TreeNode* stack2[100];
int top1 = -1;
int top2 = -1;
TreeNode* p = root;
stack1[++top1] = p;
while (top1 != -1) {
p = stack1[top1--];
stack2[++top2] = p;
TreeNode* child = getFirstChild(p);
while (child != NULL) {
stack1[++top1] = child;
child = getNextBrother(child);
}
}
while (top2 != -1) {
printf("%c ", stack2[top2--]->data);
}
}
int main() {
// 构建左儿子右兄弟链接结构的树
TreeNode* A = createNode('A');
TreeNode* B = createNode('B');
TreeNode* C = createNode('C');
TreeNode* D = createNode('D');
TreeNode* E = createNode('E');
TreeNode* F = createNode('F');
A->firstChild = B;
B->nextBrother = C;
C->nextBrother = D;
C->firstChild = E;
E->nextBrother = F;
// 使用递归后根遍历算法
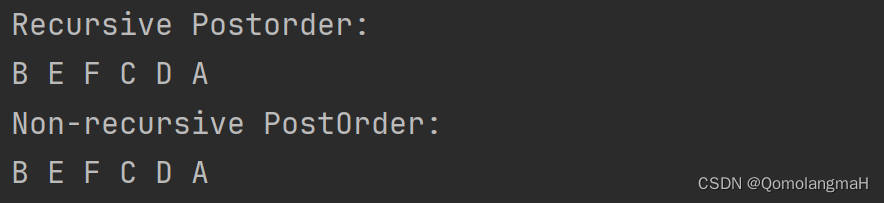
printf("Recursive Postorder: \n");
PostOrder(A);
printf("\n");
// 使用非递归后根遍历算法
printf("Non-recursive PostOrder: \n");
NorecPostOrder(A);
printf("\n");
// 释放树节点
freeTree(A);
return 0;
}