​

摘要：布尔可满足性问题（Boolean Satisfiability Problem，简称SAT问题）是逻辑学和计算机科学中的一个问题，它的目的是确定是否存在一种解释，使给定的布尔公式成立。换句话说，它询问给定布尔公式的变量是否可以被一致地替换为真值或假值，使公式求值为真。如果是这样，那么这个公式就是可满足的。另一方面，如果不存在这样的赋值，那么该公式所表示的函数对于所有可能的变量赋值都为假，该公式不可满足1。

追根溯源，SAT是第一个已知的NP-Complete问题，多伦多大学的Stephen Cook在1971年，国家科学院的Leonid Levin在1973年均独立证明了这一问题。在此之前，NP-Complete问题的概念甚至不存在。另外，证明显示复杂性类NP中的每个决策问题都可以简化为CNF公式的SAT问题，有时也称为“CNFSAT”。

值得注意的是，SAT问题是计算机科学领域最基本的问题之一，有着重要的理论意义和实际应用。在理论研究中，SAT问题是一个经典的判定问题，同样是第一个被证明为NP-Complete的问题。这个决策问题在包括理论计算机科学、复杂性理论、算法、密码学和人工智能等计算机科学的各个领域都至关重要。

在现实场景应用中，SAT是很多工业场景里面的核心工具。尤其在一些包括芯片测试、电路等价性验证、电路模型检测、智慧园区及无线设备的布局、操作系统、航空等对精确度要求很高的核心领域，都需要SAT求解器的重磅参与。例如，芯片SAT分析是一种系统级应用测试分析方法，通过对芯片的性能和可靠性进行全面的测试和分析，以评估芯片在实际应用中的表现。

另外，在腾讯地图中的语音序列调度中，采用SAT算法中的约束加权方法，播报失败率从6.20%可降至2.85%，降幅54%，同时把地图路网更新的内存消耗量降低一半，更新周期缩短一半。

5月16日，北京玻色量子科技有限公司（以下简称“玻色量子”）在新品发布会上推出的100量子比特相干光量子计算机真机——“天工量子大脑”，旨在快速、且高效地求解NP难的组合优化问题，尤其是Ising问题🔗。而布尔可满足性(SAT)和最大可满足性(Max-SAT)是NP-Complete问题和NP难问题的一类，两者同等重要且更切合实际的组合优化问题。

目前，求解布尔SAT的方法有很多，比如量子退火和经典的随机局部搜索(SLS)求解器。然而，它们都需要巨量步骤来解决困难的SAT问题，这将耗费大量的时间和精力。随着量子计算技术的发展，一个SAT问题可以转化为一个Ising/QUBO问题，从而可由玻色量子的“天工量子大脑”快速高效地求出全局最优解。

那么，为了更清楚的理解SAT问题，下面首先介绍一些基本术语。

基本定义和术语

SAT问题，简单地说就是确定是否存在满足给定布尔公式解释的问题，它需要判断给定布尔公式的变量是否可以一致地替换为值 TRUE 或 FALSE，以使公式的计算结果为 TRUE。如果是这种情况，则公式称为“满足”。否则，若不存在这样的赋值，则公式表示的函数对于所有可能的变量赋值都是 FALSE，并且公式是不满足的。例如，公式“a AND NOT b”是可以满足的，因为可以找到值a = TRUE和b = FALSE，这使得（a AND NOT b）= TRUE。相反，“a AND NOT a”是无法被满足的，因为找不到这样的a的值。

命题逻辑公式，也称为布尔表达式，由变量，运算符AND（连接，也用∧表示）、OR（分离，∨）、NOT（否定，¬）和括号构成。如果通过为其变量分配适当的逻辑值（即TRUE，FALSE）可以使公式为TRUE，则称该公式是可满足的。给定公式，布尔可满足性问题（SAT）是检查它是否可满足。

布尔可满足性问题有几种特殊情况，其中公式需要具有特定结构。文字是一个变量，称为正文字，或变量的否定，称为负文字。子句是文字（或单个文字）的分离。如果一个子句最多包含一个正文字，则该子句称为Horn子句。如果公式是条款（或单个子句）的连接，则公式为合取范式（CNF）。

例如，x1是正文字，¬x2是负文字，x1∨¬x2是子句，（x1∨¬x2）∧（¬x1∨x2∨x3）∧x1是联合范式的公式；它的第一和第三个条款是Horn条款，但它的第二个条款不是。

最大可满足性问题（Max-SAT）是确定给定布尔公式（以合取范式表示）中最多有多少个子句可以通过对公式变量赋真值来使其成立。它是布尔可满足性问题的推广，后者询问是否存在一种真值赋值使所有子句都成立。

问题描述

2-SAT和3-SAT问题是SAT问题的两种形式，它们的区别在于每个子句中包含的变量数量不同。

具体来说，2-SAT问题中每个子句最多包含两个变量，形如(a∨b)、（¬a∨c）等，其中∨表示逻辑或，¬表示逻辑非。而3-SAT问题中每个子句最多包含三个变量，形如(a∨¬b∨c)、(¬a∨b∨¬c)等。

因为2-SAT问题中每个子句最多包含两个变量，所以可以使用一些特殊的算法（如Kosaraju算法和Tarjan算法）在多项式时间内求解。而3-SAT问题则是NP-Complete问题，目前还没有已知的多项式时间算法可以解决。由于二元变量存在（0/1或者-1/+1）表达形式的区别，常见模型有两种建模思路，在这里分别进行说明。

建模思路一

我们以Max 2-SAT问题进行讨论，将文字表示为0/1的变量，建立QUBO模型。每个子句由两个文字组成，如果其中一个或两个文字都为真，则满足一个子句。对于这个问题有三种可能的子句类型，每一种都有一个传统的约束，如果子句是真的，则必须满足。

下面是三种常见的转换情况：

① 无负文字

例如：(xi∨xj)

传统约束：(xi+xj)≥1

QUBO惩罚项：(1-xi-xj+xixj)

② 一个负文字

例如：（xi∨¬xj）

传统约束：xi+¬xj≥1

QUBO惩罚项：（xj-xixj)

③ 两个负文字

例如：（¬xi∨¬xj）

传统约束：¬xi+¬xj≥1

QUBO惩罚项：（xixj）

注：由于变量xj为1/0，所以¬xj=1-xj

对于每个子句类型，如果满足传统约束，则对应的惩罚等于0；如果不满足传统约束，则二次惩罚等于1。给定这种一一对应的关系，我们可以通过等价地最小化不满足的子句数量来逼近子句数量最大化问题。通过这种形式我们可以构建一个QUBO模型。

所以，对于给定的Max 2-SAT算例，我们可以添加与问题子句相关的二次惩罚项，得到一个我们想要最小化的复合惩罚函数。由于惩罚项均为二次型，因此该惩罚函数采用QUBO模型形式，min y=xTQx。如果在最小化QUBO模型时等于零，这意味着我们有一个满足所有子句的解；如果等于5，这意味着我们有一个满足除5以外的所有子句的解。

我们用以下4个变量和12个子句的例子来说明这个算例的建模和求解过程。

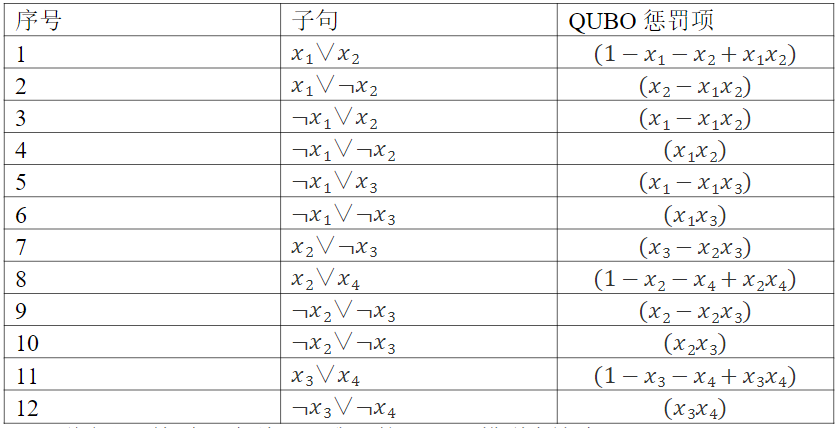
将惩罚项加在一起给出了我们的QUBO模型表达式：

min y=3+x1-2x4-x2x3+x2x4+2x3x4      (1)       

或QUBO模型的矩阵形式：

            min y=3+xTQx                (2)

则Q矩阵表达为

求解这个QUBO模型可以得到y=3-2=1，其中x1=x2=x3=0，x4=1。意思是除一个子句外的所有子句都满足。

注：上述QUBO方法已在Kochenberger等人的研究中得到成功应用[2]，研究解决了含有数百个变量和数千个子句的Max 2-SAT问题。这种方法求解Max 2-SAT问题的一个有趣的特点是，得到的待求解QUBO模型的大小与问题中的子句数无关，仅由变量的个数决定。因此，一个含有200个变量和30000个子句的Max 2-SAT问题可以建模为一个只含有200个变量的QUBO模型并求解。

建模思路二

为了更好地理解这个问题，我们将文字表示为-1/1的变量，继续讨论一个3-Sat问题。

我们讨论一个3-Sat子句：

x1∨x2∨x3

该子句通过引入-1/1辅助变量可以映射成二次函数：

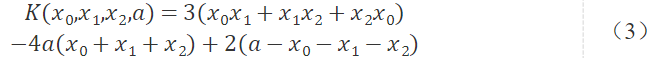
在x0，x1，x2的任意取值中，都有一个使得K最小的值a。如果我们假设a总是被设置为这个最优值，那么除了x0=x1=x2=-1时能量为+1外，其他取值的最低能量都是-7。下表总结了有关变量的取值，其中加粗的数字是给定x0，x1，x2变量的最低可能能量。

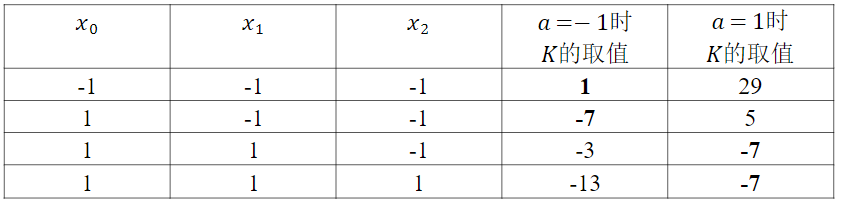
使用这种方法，如果xi在子句中被否定，我们可以通过将xi替换为-xi来编码任意3-Sat子句。现在，如果我们对求和这些每个子句对应的二次函数，我们可以得到一个关于Nxi自旋变量和Maj辅助自旋的二次函数，从而得到一个大小为N+M的Ising/QUBO问题。如果该问题是可满足的，那么最小的Ising能量将是-7M，如果该问题是不可满足的问题，那么最小的Ising能量为-7Msat，其中Msat是可满足子句的个数。

问题拓展

MAX-SAT是最大可满足性问题，是SAT问题的推广。它要求最大数量的条款，任何转让都可以满足。它具有有效的近似算法，但是NP时间难以精确解决。

在量子计算领域，2023年6月，NTT最新的研究提出了一种相干SAT求解器(CSS)的新技术。使用图形处理器(GPU)实现的Cyber-CSS与现有的SLS求解器(如probSAT)相比有一定的竞争力。未来通过量子计算实现SAT问题的快速求解将成为一种新的有效方法。

如今，玻色量子已基于自研的相干光量子计算机真机——“天工量子大脑”在SAT问题求解上具有显著的算力优势，代表了其在NP-Complete问题上的实用性，以进一步拓展更多可实用化量子计算应用场景。

玻色量子还将启动“燎原计划”开发者平台，并持续对外开放“天工量子大脑”的真机测试，热忱欢迎更多不同领域的研究伙伴前来了解相干量子计算的原理和能力，在此基础上展开共同研发，用量子计算去解决更多真实场景中的问题，让量子计算的超强算力能真正服务于各行各业，满足未来时代对于计算的需求。

[参考文献]

[1] Glover, Fred, Kochenberger, Gary, Du, Yu. Quantum Bridge Analytics I: a tutorial on formulating and using QUBO models[J]. 4OR: Quarterly Journal of the Belgian, French and Italian Operations Research Societies,2019,17(4):335-371. DOI:10.1007/s10288-019-00424-y.

[2] Kochenberger G , Glover F , Alidaee B ,et al.Using the unconstrained quadratic program to model and solve Max 2-SAT problems[J].International Journal of Operational Research, 2005, 1(1/2):89--100.DOI:10.1504/IJOR.2005.007435.

[3] Reifenstein S, Leleu T, McKenna T, et al. Coherent SAT solvers: a tutorial[J]. Advances in Optics and Photonics, 2023, 15(2): 385-441.

[4] 百度百科

https://baike.baidu.com/item/%E5%B8%83%E5%B0%94%E5%8F%AF%E6%BB%A1%E8%B6%B3%E6%80%A7%E9%97%AE%E9%A2%98/4715567?fr=aladdin