前言

1、子集||
2、递增子序列
3、全排列
4、全排列||

一、子集 II（力扣90）

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。返回的解集中，子集可以按任意顺序排列。
在这里插入图片描述
思路：

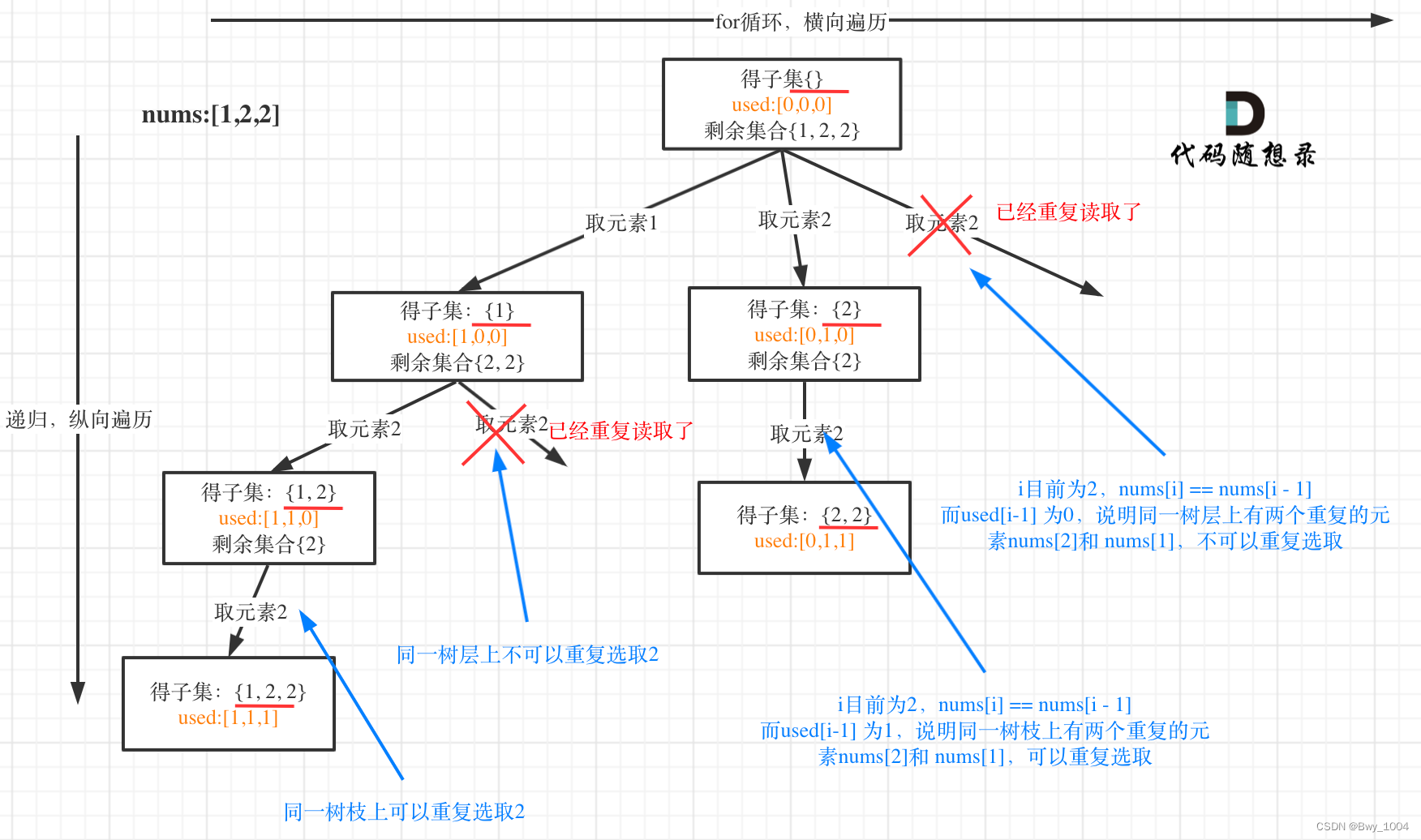
与子集问题相比，关键在于去重问题
去重问题的解决与组合总和||中的解决方式一摸一样。“树层去重”

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> paths = new LinkedList<>();
    boolean[] used;
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        used = new boolean[nums.length];
        Arrays.fill(used,false);
        Arrays.sort(nums);
        backtracking(nums,0,used);
        return res;
    }
    public void backtracking(int[] nums,int startIndex,boolean[] used){
        res.add(new ArrayList<>(paths));

        for(int i=startIndex;i<nums.length;i++){
            if(i>0 && nums[i]==nums[i-1]&&used[i-1]==false){
                //去重
                continue;
            }
            paths.add(nums[i]);
            used[i]=true;
            backtracking(nums,i+1,used);
            //回溯
            used[i]=false;
            paths.removeLast();
        }
    }
}

二、递增子序列（力扣491）

给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中至少有两个元素。你可以按任意顺序返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。
在这里插入图片描述
本题求自增子序列，是不能对原数组进行排序的，排完序的数组都是自增子序列了。

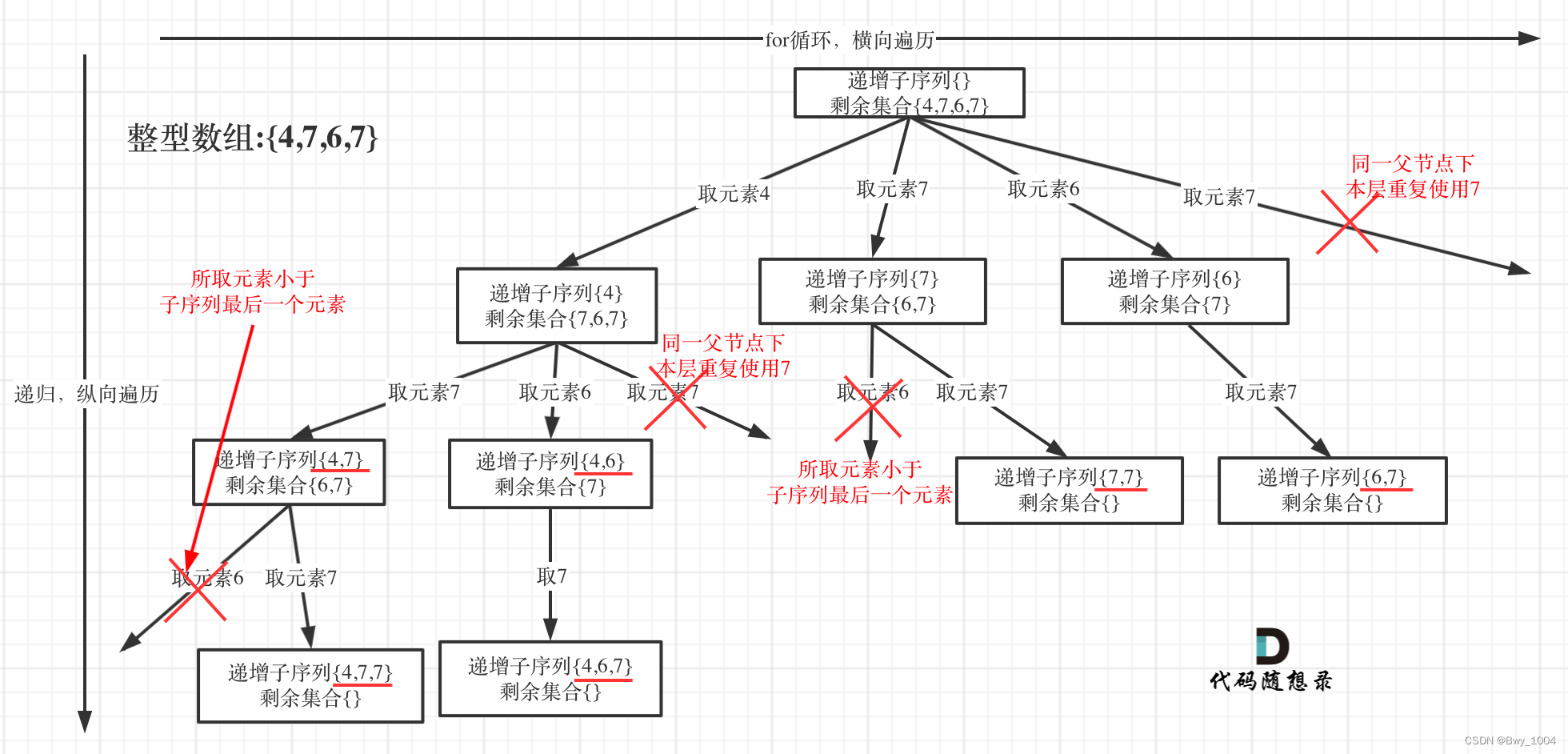
进行去重操作，记录使用过的元素使用map或者数组都可以

used[nums[i]+100]=1;为什么没有回溯
原因在于每一层我都需要去重新记录元素是否被访问过
used是局部变量
是记录本层元素是否重复使用，新的一层used都会重新定义（清空），所以要知道used只负责本层！

数组去重

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> paths = new LinkedList<>();

    public List<List<Integer>> findSubsequences(int[] nums) {
        backTracking(nums,0);
        return res;
    }
    public void backTracking(int[] nums,int startIndex){
        //收集结果集
        if(paths.size()>1){
            res.add(new ArrayList<>(paths));
        }
        int[] used = new int[201];
        for(int i=startIndex;i<nums.length;i++){
            if(!paths.isEmpty()&&nums[i]<paths.get(paths.size()-1) || (used[nums[i]+100]==1)){
                continue;
            }
            used[nums[i]+100]=1;
            paths.add(nums[i]);
            backTracking(nums,i+1);
            paths.removeLast();    
        }
    }
}

map去重

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> paths = new LinkedList<>();

    public List<List<Integer>> findSubsequences(int[] nums) {
        backTracking(nums,0);
        return res;
    }
    public void backTracking(int[] nums,int startIndex){
        //收集结果集
        if(paths.size()>1){
            res.add(new ArrayList<>(paths));
        }
        HashMap<Integer,Integer> map = new HashMap<>();
        for(int i=startIndex;i<nums.length;i++){
            if(!paths.isEmpty()&&nums[i]<paths.get(paths.size()-1)){
                continue;
            }
            if(map.getOrDefault(nums[i],0)>=1) continue;
            map.put(nums[i],map.getOrDefault(nums[i],0)+1);
            paths.add(nums[i]);
            backTracking(nums,i+1);
            paths.removeLast();    
        }
    }
}

在这里插入图片描述

三、全排列（力扣46）

给定一个不含重复数字的数组 nums ，返回其所有可能的全排列。你可以按任意顺序返回答案。
在这里插入图片描述
思路：
全排列问题不再有startIndex 每一次都需要从0开始

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> paths = new LinkedList<>();
    public List<List<Integer>> permute(int[] nums) {
        backtracking(nums);
        return res;
    }
    public void backtracking(int[] nums){
        if(paths.size()==nums.length){
            //收集结果
            res.add(new ArrayList<>(paths));
            return;
        }
        for(int i=0;i<nums.length;i++){
           if(!paths.contains(nums[i])){
               paths.add(num);
               backtracking(nums);
               paths.removeLast();
           } 
        }
    }
}

在这里插入图片描述

四、全排列||（力扣47）

给定一个可包含重复数字的序列 nums ，按任意顺序返回所有不重复的全排列。
在这里插入图片描述
思路：
在上一题的基础上，增加几行去重代码即可

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> paths = new LinkedList<>();
    boolean[] used;
    public List<List<Integer>> permuteUnique(int[] nums) {
        used = new boolean[nums.length];
        Arrays.fill(used,false);
        Arrays.sort(nums);
        backTracking(nums,used);
        return res;
    }
    public void backTracking(int[] nums,boolean[] used){
        if(paths.size()==nums.length){
            //收集结果
            res.add(new ArrayList<>(paths));
            return ;
        }
        for(int i=0;i<nums.length;i++){
            if(i>0 && nums[i]==nums[i-1] && used[i-1]==false){
                continue;
            }
            if(used[i]==false){
                paths.add(nums[i]);
                used[i]=true;
                backTracking(nums,used);
                //回溯
                used[i]=false;
                paths.removeLast();
            }
        }
    }
}