《算法通关村——数论问题解析》

news2024/11/15 8:43:44

《算法通关村——数论问题解析》

辗转相除法

辗转相除法又叫做欧几里得算法,是公元前 300 年左右的希腊数学家欧几里得在他的著作《几何原本》提出的。最大公约数(greatest common divisor，简写为gcd），是指几个数的共有的因数之中最大的一个，例如 8 和 12 的最大公因数是 4，记作 gcd(8,12)=4。辗转相除法最重要的规则是，若 r 是 a ÷ b 的余数, 则gcd(a,b) = gcd(b,r)。例如计算 gcd(546, 429)：

由于 546=1(429)+117
429=3(117)+78
117=1(78)+39
78=2(39)
因此 
gcd(546, 429) 
=gcd(429, 117) 
=gcd(117, 78) 
=gcd(78, 39) 
=39

    public static int  gcd(int a,int b){
        int k = 0;
        do{
            k = a % b;
            a = b;
            b= k;
        }while(k==0);
        return k;
    }

素数和合数

我们看一下素数和合数的问题。素数又称为质数，素数首先要满足大于等于2，并且除了1和它本身之外，不能被任何其他自然数整除。其他数都是合数。比较特殊的是1即非素数，也非合数。2是唯一的同时为偶数和素数的数字。

有了定义，自然第一个问题就是如何判断一个正整数是否为素数。题目要求：给定一个正整数n(n<10^9)，判断它是否为素数。

基本的方式是从2开始依次与n取余测试，看看是否出现n%i==0的情况，如果出现了则说明当前的n能被i整除，所以就不是。理论上一直测试到n-1，假如都不是，那就是素数了。

而事实上不需要测试这么多，只要从2开始遍历一直到n^(1/2)就可以，不用执行到n-1。这个是有明确的数学证明的，我们不再赘述，如果不知道请回家问高中老师。所以实现代码就是：

boolean isPrime(int num) {
  int max = (int)Math.sqrt(num);
  for (int i = 2; i <= max; i++) {
        if (num % i == 0) {
             return false;
         }
      }
   return true;
    }

埃氏筛

基本思想是如果 x是质数，那么大于 x 的 xy的倍数 2x. 3x… 一定不是质数，因此我们可以从这一点入手。如下图所示:
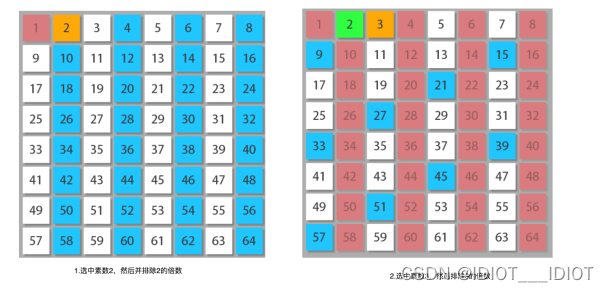
在这里插入图片描述

我们先选中数字2，2是素数，然后将2的倍数全部排除（在数组里将该位置标记为0就行了）。

接着我们选中数字3，3是素数，然后将3的倍数全部排除。

接着我们选择数字5，5是素数，然后将5的倍数全部排除。

接着我们选择 7，11，13一直到n，为什么 4 、6、8 、9 …不会再选择了呢？因为我们已经在前面的步骤中，将其变成0了。所以实现代码如下：

public static int countPrimes(int n) {
    int[] primes = new int[n];
    Arrays.fill(primes,1);
    int count = 0;
    for(int i = 2;i<n;i++){
        if(primes[i]==1){
            count ++;
            if((long)i*i < n){ // 这里是先转为long在计算否则会超出int最大数
                for(int j = i* i ;j<n;j+=i){ // 这里都只要 i * i开始就可以了，因为前面的都被前面的数据给覆盖了。
                    primes[j] = 0;
                }
            }
        }
    }
    return count;

}

丑数问题

我们把只包含质因子 2、3 和 5 的数称作丑数（Ugly Number），求按从小到大的顺序的第 n 个丑数。

示例：
输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数.根据丑数的定义，0 和负整数一定不是丑数。

当 n>0 时，若 n 是丑数，则 n 可以写成 n = 2^a + 3^b + 5^c 的形式，其中 a,b,c 都是非负整数。特别地，当 a,b,c 都是 000 时，n=1。

为判断 n 是否满足上述形式，可以对 n 反复除以 2,3,5，直到 n 不再包含质因数 2,3,5。若剩下的数等于 1，则说明 n 不包含其他质因数，是丑数；否则，说明n包含其他质因数，不是丑数。

public class IsUgly {
    public static boolean isUgly(int n){
        int[] values = {2,3,5};
        for(int value : values){
            while(n%value==0){
                n/=value;
            }
        }
        return n==1;
    }

    public static void main(String[] args) {
        System.out.println(isUgly(10));
    }
}