排序
- 排序的概念
- 常见的排序算法
- 直接插入排序
- 希尔排序(缩小增量排序)
- 选择排序
- 堆排序
- 冒泡排序
- 快排(递归)
- 霍尔版本
- 挖坑法
- 前后指针法
- 快排(非递归)
- 归并排序(递归)
- 归并排序(非递归)
- 计数排序
排序的概念
排序:将杂乱无章的数据元素,通过一定的方法按关键字顺序排列的过程叫做排序
内部排序:数据全部放在内存中的排序
外部排序:由于数据太多不能全部放在内存中,需要借助外存的排序
常见的排序算法
比较排序
插入排序:直接插入排序,希尔排序
选择排序:直接选择排序,堆排序
交换排序:冒泡排序,快速排序
归并排序:归并排序
非比较排序
计数排序
直接插入排序
思路:
直接插入排序是指在待排序的元素中,假设前面n-1(其中n>=2)个数已经是排好顺序的,现将第n个数插到前面已经排好的序列中,然后找到合适自己的位置,使得插入第n个数的这个序列也是排好顺序的
算法实现
void Insertsort(int* a, int n)
{
int i = 0;
for (i = 0; i < n - 1; i++)
{
//[0,end],在end+1位置上插入一个数,使[0,end+1]有序
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
//跳出循环有两种可能
//1.end已经越界,此时end==-1
//2.找到比tmp小的数据
a[end + 1] = tmp;
}
}
图形展示
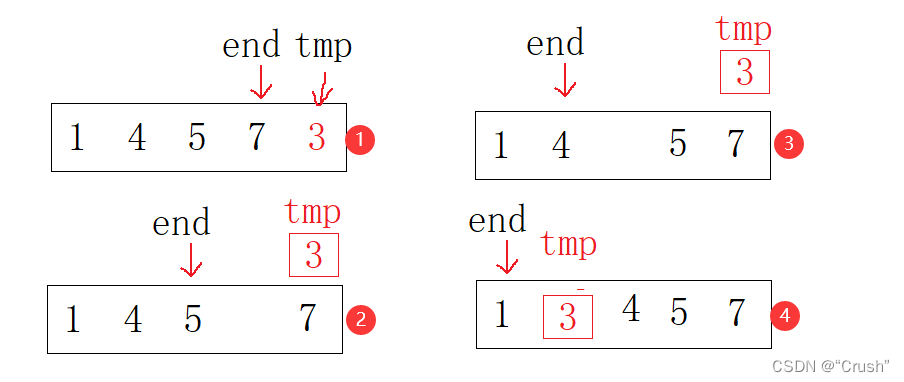
运行结果

直接插入排序的特点
- 元素集合越接近有序,插入排序的时间效率便越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
希尔排序(缩小增量排序)
思路:
先选定一个整数,把待排序的数据按一定距离分成若干小组,对每一组内的数据进行排序;然后逐渐减小距离,重复上面的操作,直到距离为1所有数据被分到一组,结束排序
图形展示
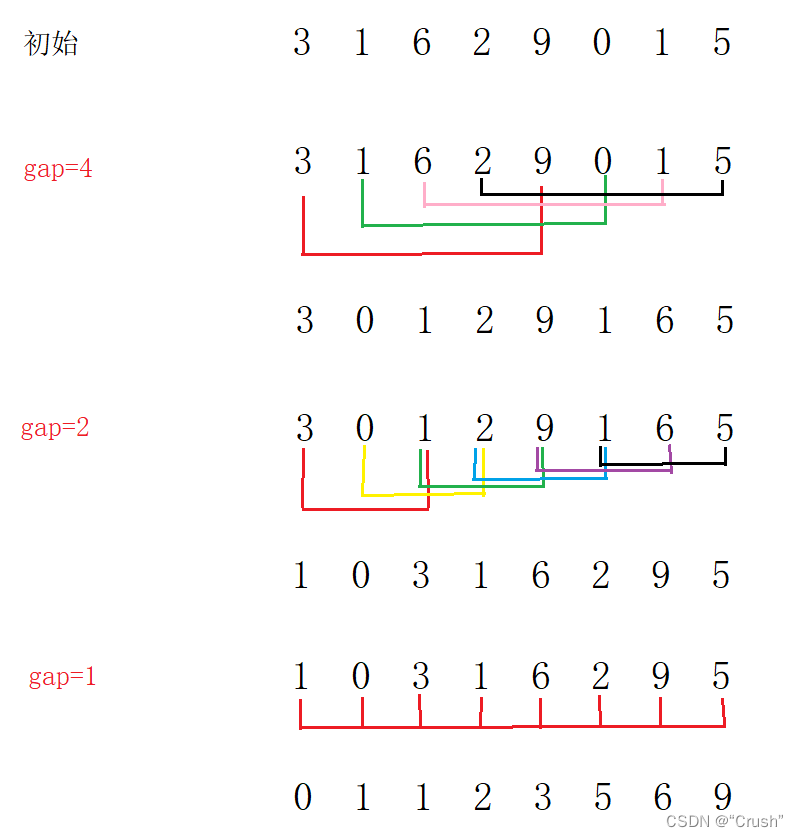
算法实现
void Shellsort(int* a, int n)
{
int gap = n;
while (gap > 0)
{
gap /= 2;
int i = 0;
//gap组数据依次多组并排
for (i = 0; i < n - gap; i++)
{
int end = i;
//[0,end],在end+gap位置上插入一个数据使[0,end+gap]有序
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
运行结果
希尔排序的特点
- 希尔排序是对插入排序的优化
- 当gap>1是称为预排序,目的便是使数组接近有序;gap越大,大的数据可以越快跳到后面,小的数据可以越快跳到前面;gap越小,数据跳的越慢,但也越接近有序;当gap==1时,数组已经接近有序,排序就更加的快
- 由于gap的取值没有统一的规定,便导致时间复杂度不易计算
- 稳定性:不稳定
选择排序
思路:
每次从待排序的数据中选出最小的和最大的数据,若这两个数据不是这组数据的第一个,最后一个数据,则将这两个数据与第一个,最后一个数据进行交换;然后再从剩余的数据中重复此操作,直到排完所有数据

算法实现
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void Selectsort(int* a, int n)
{
int left = 0;
int right = n - 1;
while (right > left)
{
int min = left;
int max = left;
int i = 1;
for (i = left+1; i <= right; i++)
{
if (a[i] > a[max])
{
max = i;
}
if (a[i] < a[min])
{
min = i;
}
}
Swap(&a[left], &a[min]);
//如果最大的数据在第一个位置,需要进行调整
if (max == left)
{
max = min;
}
Swap(&a[right],&a[max]);
left++;
right--;
}
}
选择排序的特点
- 效率不高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
堆排序
在上一篇博客中有详细介绍堆排序,这里就不再赘述需要注意的是
升序:建大堆
降序:建小堆
算法实现
void Adjustdown(int* a, int n, int i)
{
int minchild = 2 * i + 1;
while (minchild < n)
{
if (minchild + 1 < n && a[minchild + 1] > a[minchild])
{
minchild++;
}
if (a[minchild] > a[i])
{
Swap(&a[minchild], &a[i]);
i = minchild;
minchild = 2 * i + 1;
}
else
{
break;
}
}
}
void Heapsort(int* a, int n)
{
int i = 0;
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
//向下调整
Adjustdown(a, n, i);
}
i = 1;
while (i < n)
{
Swap(&a[0], &a[n - i]);
Adjustdown(a, n - i, 0);
i++;
}
}
堆排序的特点
- 效率很高
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
冒泡排序
思路:
它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果顺序(后一个数大于前一个数)错误就把他们交换过来。走访元素的工作是重复地进行,直到没有相邻元素需要交换,也就是说该元素列已经排序完成
就类似气泡一样,越往后越大
图形展示
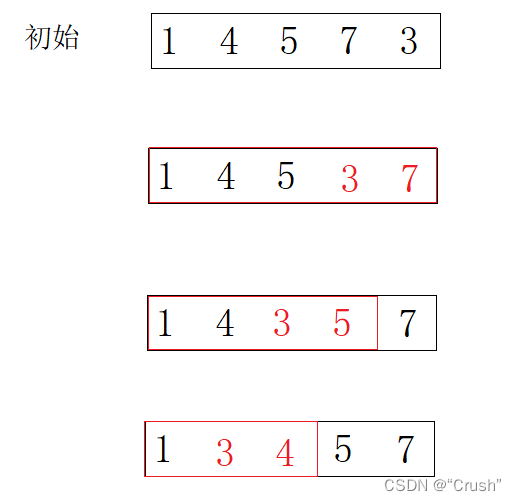
算法实现
void Bubblesort(int* a, int n)
{
int j = 0;
for (j = 1; j <= n; j++)
{
int i = 0;
int exchange = 1;
for (i = 0; i < n - j; i++)
{
if (a[i] > a[i+1])
{
Swap(&a[i], &a[i + 1]);
}
else
{
exchange = 0;
}
}
if (exchange == 1)
{
break;
}
}
}
冒泡排序的特点
- 非常容易理解
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
快排(递归)
思路:
任取待排序元素序列中的某个元素作为基准值,按照该基准值,将待排序的元素分为两个子序列,左子序列的元素全部小于基准值,右子序列的元素全部大于基准值;然后左右子序列重复此操作,直到所有将所有元素排序完 右边找小,左边找大
将整个序列按照基准值划分为左右两部分的常见方式有三种:霍尔版本,挖坑法,前后指针法
单趟排序
- 选择基准值key(一般默认选择第一个数)
- 单趟排序的结果,小的数在key左边,大的数在key右边
霍尔版本
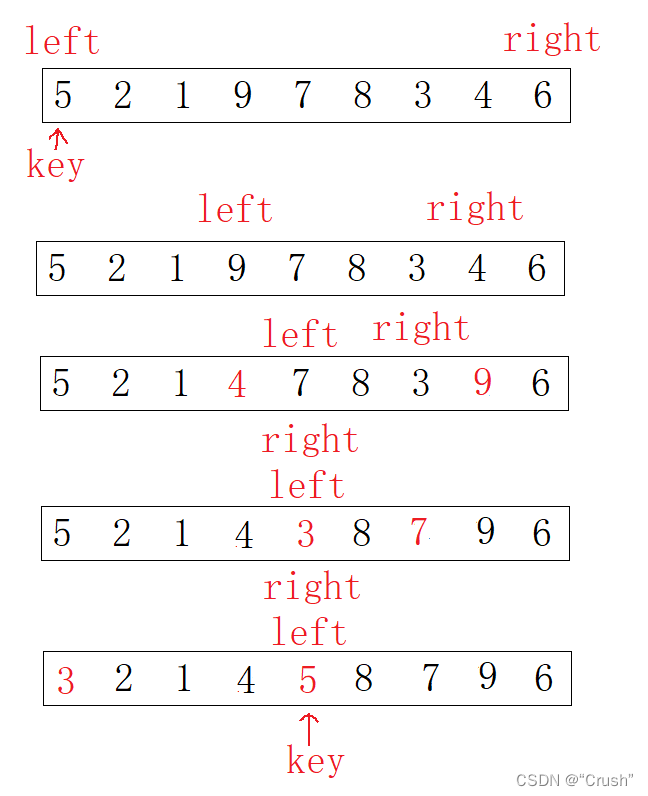
当第一个数为key时,为保证相遇位置的值一定比key小,right先走
- R找到比key小的数停下,L撞到R相遇
- L找到比key大的数与R找到比key小的数进行交换,然后停下,R撞到L相遇
每次基准值确定之后,就代表这个基准值的位置在整个排序中位置就确定好了,不需要再进行变动;接下来只需要在基准值的两边重复此操作,直到两边都只剩余一个元素,便说明排序完成
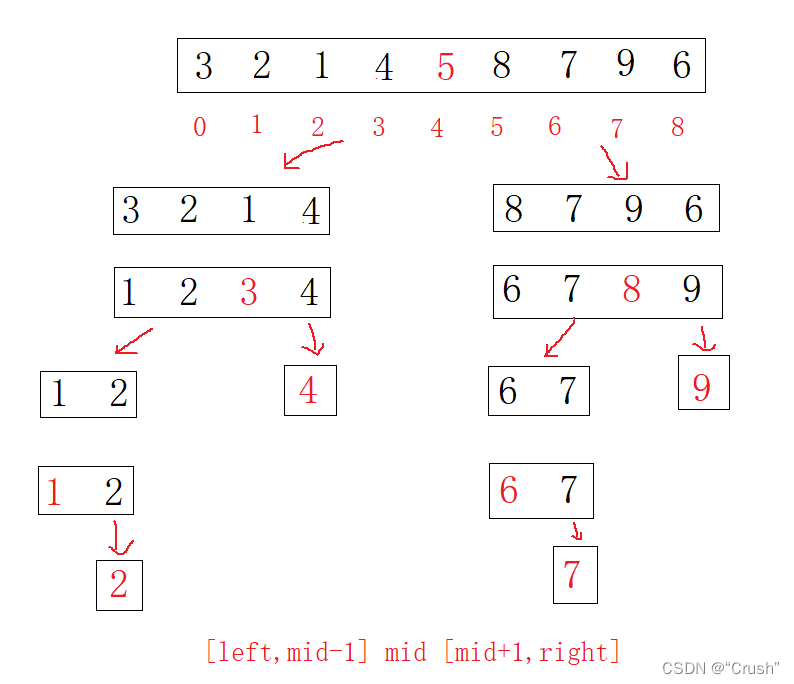
int Partsort1(int* a, int left, int right)
{
int keyi = left;
while (right > left)
{
while (right>left && a[right] >= a[keyi])
{
right--;
}
while (right>left && a[left] <= a[keyi])
{
left++;
}
Swap(&a[right], &a[left]);
}
int meet = right;
Swap(&a[meet], &a[keyi]);
return meet;
}
void Quicksort(int* a, int left, int right)
{
if (right <= left)
{
return;
}
//[left,mid-1] mid [mid+1,right]
int mid = Partsort1(a, left, right);
Quicksort(a, left, mid - 1);
Quicksort(a, mid + 1, right);
}
完成第一趟排序之后,在进行右子序列排序时,发现第一个数(基准值)相较于其他的数还是偏大的,一般情况下基准值都是选择中间值,所以需要对于选基准值进行优化
三数取中
//三数取中
int Getmidindex(int* a, int left, int right)
{
int mid = left + (right - left) / 2;
if (a[right] > a[mid])
{
if (a[mid] > a[left])
{
return mid;
}
// a[mid]<=a[left]
else if (a[right] > a[left])
{
return left;
}
// a[right]<=a[left]
else
{
return right;
}
}
else
{
if (a[right] > a[left])
{
return right;
}
// a[right]<=a[left]
else if (a[mid] > a[left])
{
return left;
}
// a[mid]<=a[left]
else
{
return mid;
}
}
}
优化后的结果
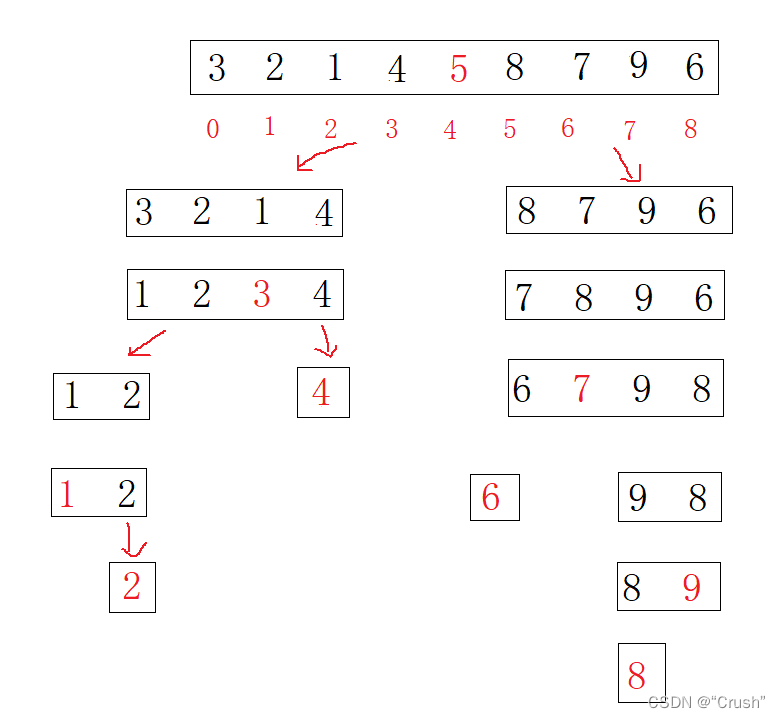
挖坑法
将第一个数据令为基准值,并将存放在临时变量中,形成一个坑位
第一次单趟排序
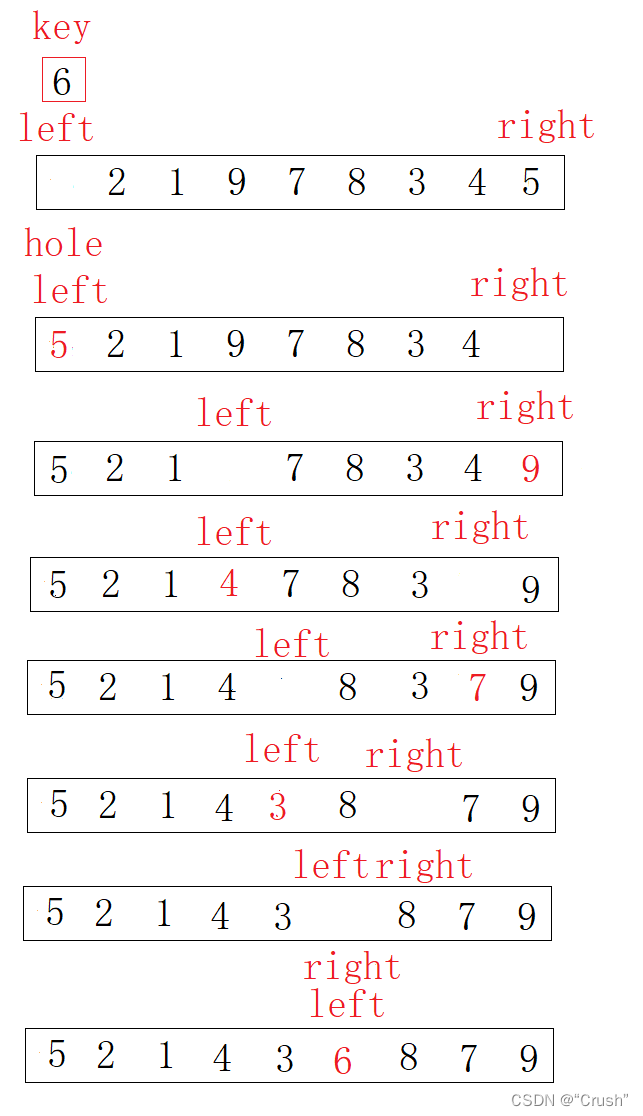
剩余的排序
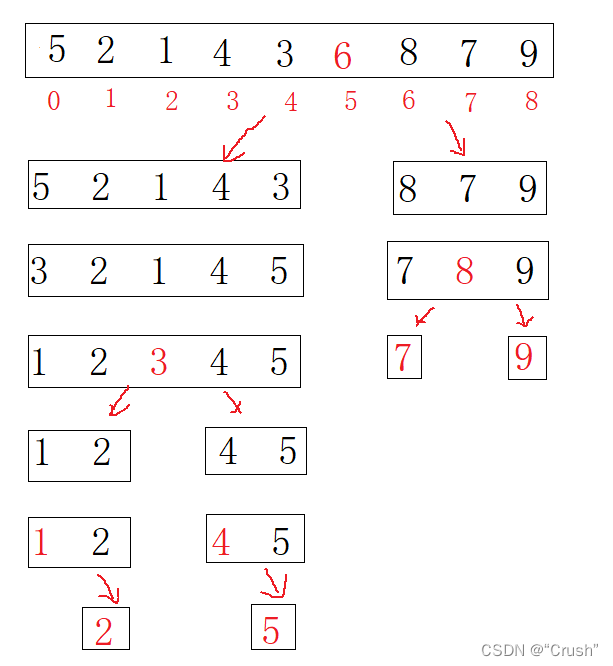
算法实现
int Partsort2(int* a, int left, int right)
{
//三数取中
int key = Getmidindex(a, left, right);
Swap(&a[left], &a[key]);
int hole = left;
while (right > left)
{
//右边找小 填到左边的坑
while (right > left && a[right] >= key)
{
right--;
}
a[hole] = a[right];
hole = right;
//左边找大 填到右边的坑
while (right > left && a[left] <= key)
{
left++;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return hole;
}
void Quicksort(int* a, int left, int right)
{
if (right <= left)
{
return;
}
int mid = Partsort2(a, left, right);
Quicksort(a, left, mid - 1);
Quicksort(a, mid + 1, right);
}
前后指针法
初始化时,prev指针指向序列的开头,cur指针指向prev指针的后一个位置
cur指针找小于key的数;prev指针要么紧跟着cur指针要么停留在比key大的数前面
cur指针遇到比key小的值时,便会停下来,++prev,交换prev和cur位置的值
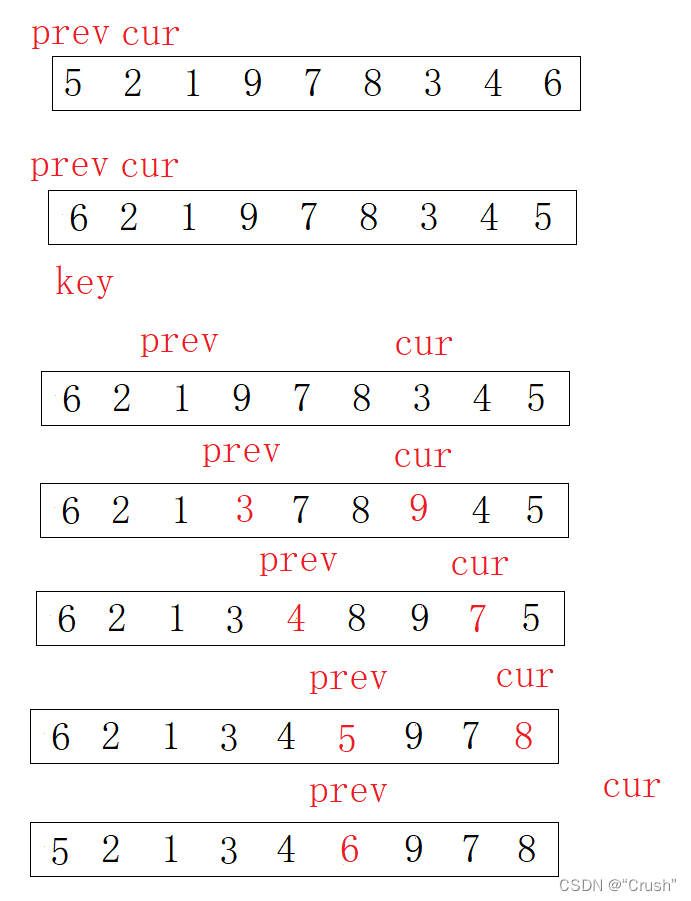
剩余的排序

算法实现
int Partsort3(int* a, int left, int right)
{
int key = Getmidindex(a, left, right);
Swap(&a[left], &a[key]);
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (a[cur] < a[key] && ++prev != cur)
{
Swap(&a[cur], &a[prev]);
}
++cur;
}
Swap(&a[prev], &a[key]);
return prev;
}
void Quicksort(int* a, int left, int right)
{
if (right <= left)
{
return;
}
int mid = Partsort3(a, left, right);
Quicksort(a, left, mid - 1);
Quicksort(a, mid + 1, right);
}
快排(非递归)

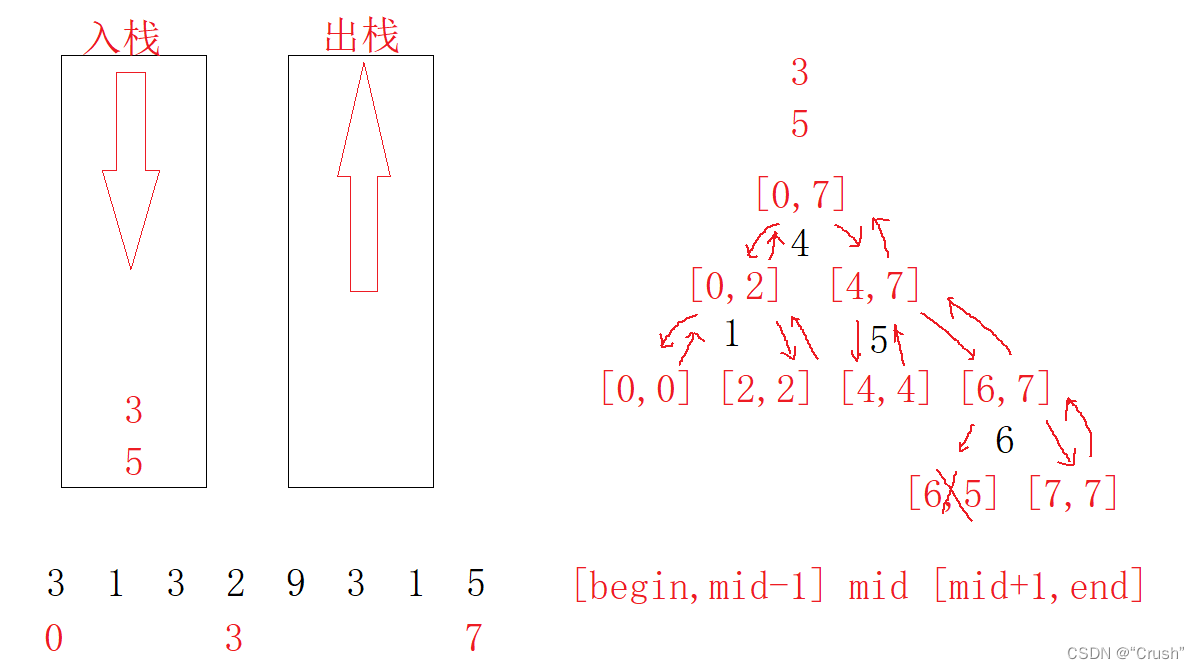
算法实现
void Quicksortnon(int* a, int begin, int end)
{
SK sk;
SKinit(&sk);
SKpush(&sk, begin);
SKpush(&sk, end);
while (!SKempty(&sk))
{
int right = SKtop(&sk);
SKpop(&sk);
int left = SKtop(&sk);
SKpop(&sk);
int key = Partsort3(a, left, right);
if (key + 1 < right)
{
//左边先入栈
SKpush(&sk, key + 1);
SKpush(&sk, right);
}
if (left < key - 1)
{
//右边后入栈
SKpush(&sk, left);
SKpush(&sk, key - 1);
}
}
}
快排的特点
- 综合性能较好,适应场景较多
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:不稳定
归并排序(递归)
思路:将已有序的子序列合并,得到完全有序的序列;若子序列未有序,先使子序列有序,再进行合并(符合分治法的思想)
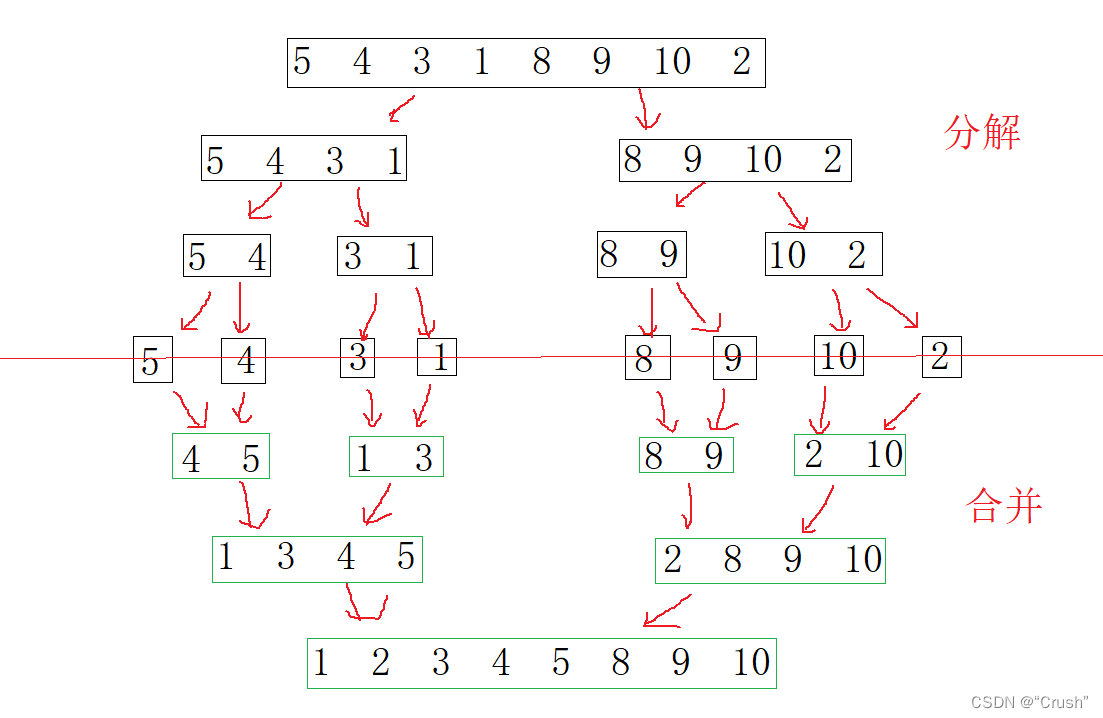
算法实现
void mergesort(int* a, int begin, int end, int* tmp)
{
//递归结束条件
if (begin >= end)
{
return;
}
//将数组平分
int mid = begin + (end - begin) / 2;
//进行递归
mergesort(a, begin, mid, tmp);
mergesort(a, mid+1, end, tmp);
//归并 取小的尾插
int begin1 = begin;
int end1 = mid;
int begin2 = mid + 1;
int end2 = end;
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
//由于两部分不可能同时结束,所以还需要对剩余的数据进行插入
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
//按照相应位置进行拷贝回原数组
memcpy(a+begin, tmp+begin, sizeof(int) * (end - begin + 1));
}
void Mergesort(int* a, int n)
{
int* tmp = (int*)malloc(n * sizeof(int));
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int begin = 0;
int end = n - 1;
//如果直接在归并函数中递归,每次都会开辟空间,导致程序崩溃
//所以创建子函数进行归并
mergesort(a, begin, end, tmp);
free(tmp);
tmp = NULL;
}
归并排序(非递归)

算法实现
void Mergesortnon(int* a, int n)
{
//开辟空间,用于排序
int* tmp = (int*)malloc(n * sizeof(int));
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)
{
int j = 0;
//每组gap个数据
for (j = 0; j < n; j += 2 * gap)
{
//取小尾插,进行归并
int begin1 = j;
int end1 = j + gap - 1;
int begin2 = j + gap;
int end2 = j + 2 * gap - 1;
int i = j;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
//由于两部分不可能同时结束,所以还需要对剩余的数据进行插入
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
//排序之后,按照位置进行拷贝回原数组
memcpy(a+j, tmp+j, (end2 - j + 1) * sizeof(int));
}
gap *= 2;
}
free(tmp);
tmp = NULL;
}
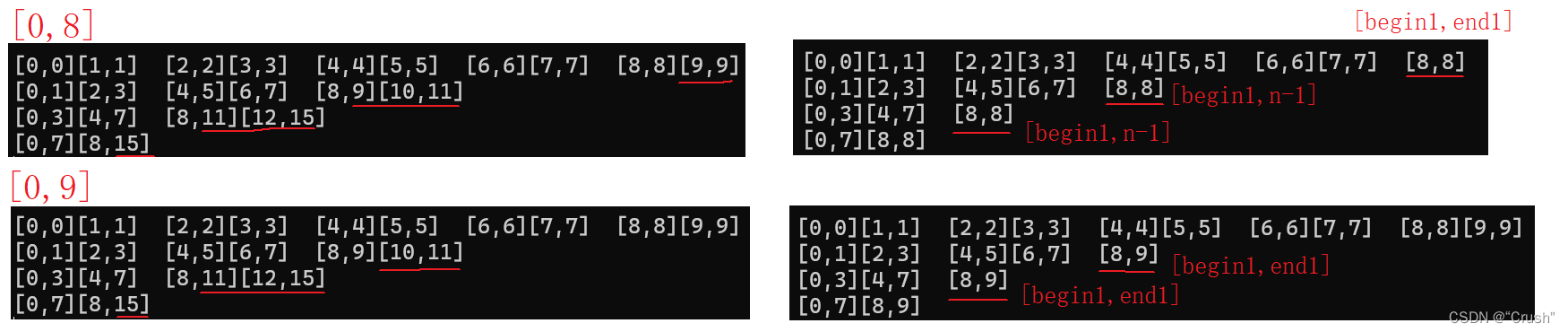
图示分析似乎没有什么问题,但如果再向数组中加一个数,结果会怎么样呢?
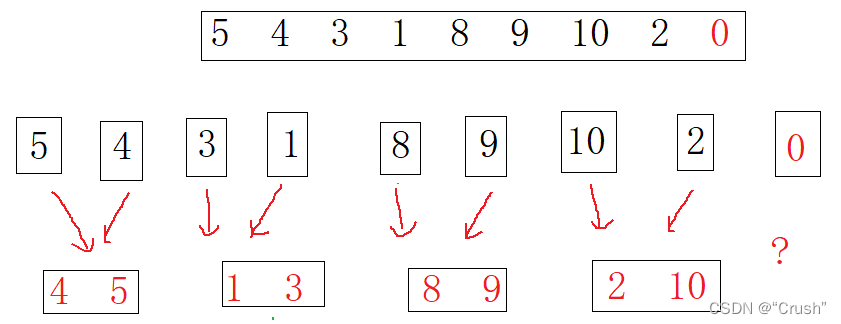
如果再向数组中加入一个数,结果又是怎么样的呢?
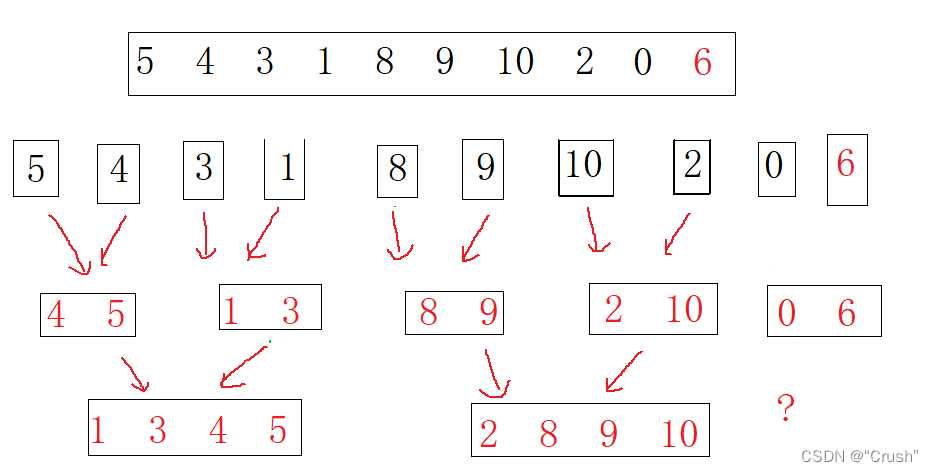
目前出现的这两种情景,上面都没有考虑到,那又该如何解决呢?
先将每次分组的数据下标打印出来,再进行分析
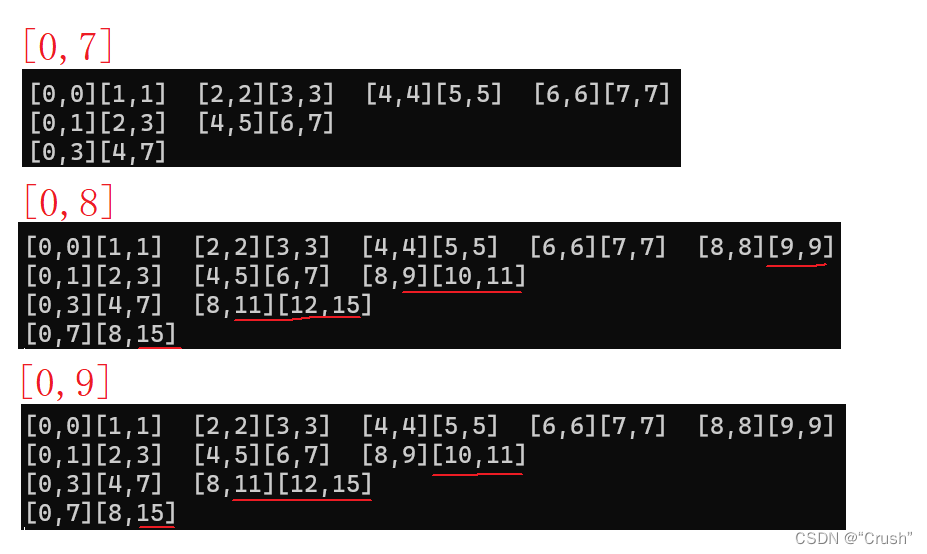
总结下来越界有三种可能
- 前一组的end1越界
- 后一组全部越界
- 后一组end2越界
解决办法
- 直接跳出循环,剩余的数据不再临时开辟的空间中进行排序
- 直接跳出循环,剩余的数据不再临时开辟的空间中进行排序
- 修改end2的数值,end2=n-1 再进行排序
优化后
void Mergesortnon(int* a, int n)
{
//开辟空间,用于排序
int* tmp = (int*)malloc(n * sizeof(int));
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)
{
int j = 0;
//每组gap个数据
for (j = 0; j < n; j += 2 * gap)
{
//取小尾插,进行归并
int begin1 = j;
int end1 = j + gap - 1;
int begin2 = j + gap;
int end2 = j + 2 * gap - 1;
int i = j;
//第一组end1越界
if (end1 >= n)
{
printf("[%d,%d]",begin1,end1);
break;
}
//第二组全部越界
if (begin2 >= n)
{
printf("[%d,%d]",begin1,end1);
break;
}
//第二组部分越界
if (end2 >= n)
{
//修改end2,继续归并
end2 = n - 1;
}
printf("[%d,%d][%d,%d] ", begin1, end1, begin2, end2);
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
//由于两部分不可能同时结束,所以还需要对剩余的数据进行插入
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
//排序之后,按照位置进行拷贝回原数组
memcpy(a+j, tmp+j, (end2 - j + 1) * sizeof(int));
}
gap *= 2;
printf("\n");
}
free(tmp);
tmp = NULL;
}
归并排序的特点
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
计数排序
思路:
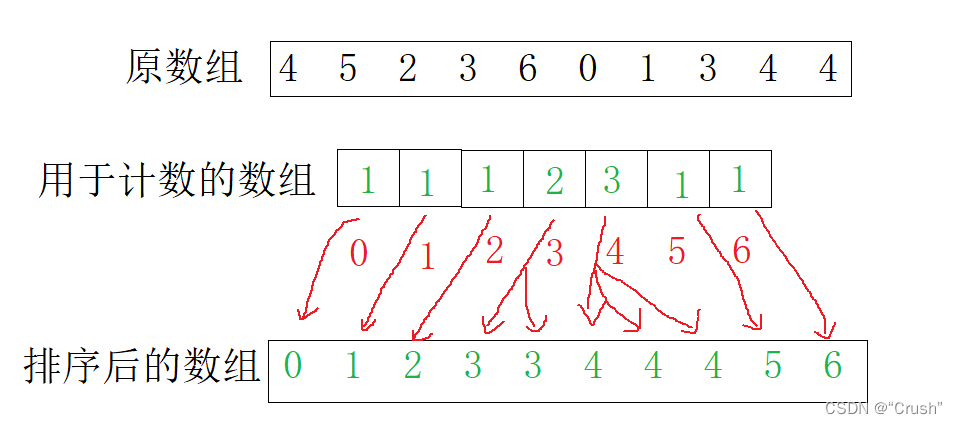
先统计相同元素出现的次数,然后开辟相对大小的空间(最大值-最小值+1),将相同元素按照对应的下标中赋以其出现的次数
用于计数的数组的下标时其对于的值(相对)的个数,某个值出现几次,便会被计数几次
算法实现
void Countsort(int* a, int n)
{
int max = a[0];
int min = a[0];
int i = 0;
for (i = 0; i < n; i++)
{
if (a[i] > max)
{
max = a[i];
}
if (a[i] < min)
{
min = a[i];
}
}
int range = max - min + 1;
//统计次数
int* tmp = (int*)malloc(sizeof(int) * range);
memset(tmp, 0, sizeof(int) * range);
for (i = 0; i < n; i++)
{
tmp[a[i] - min]++;
}
//排序
int j = 0;
for (i = 0; i < range; i++)
{
while (tmp[i]--)
{
a[j] = i + min;
j++;
}
}
free(tmp);
tmp = NULL;
}
计数排序的特点
- 当数据范围比较集中时,效率很高
- 时间复杂度:O(N,range)
- 空间复杂度:O(range)
- 稳定性:稳定


![[附源码]java毕业设计静谧空间自习室预订系统](https://img-blog.csdnimg.cn/6cb003ccc2e8438a82deb1695780eee2.png)





![[附源码]java毕业设计基于篮球云网站](https://img-blog.csdnimg.cn/669010b0ed304d2c8347016b811079c1.png)

