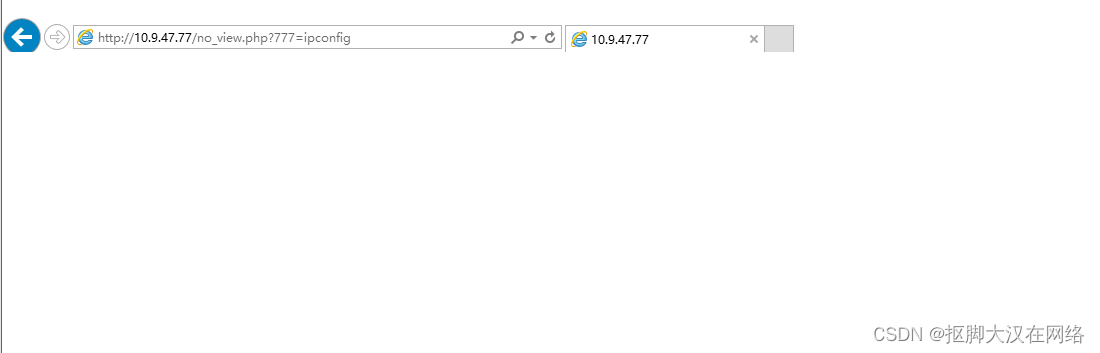
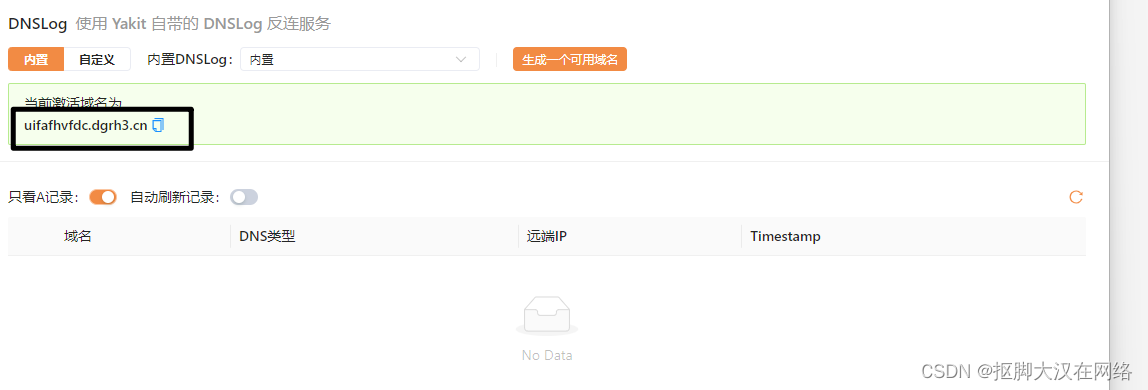
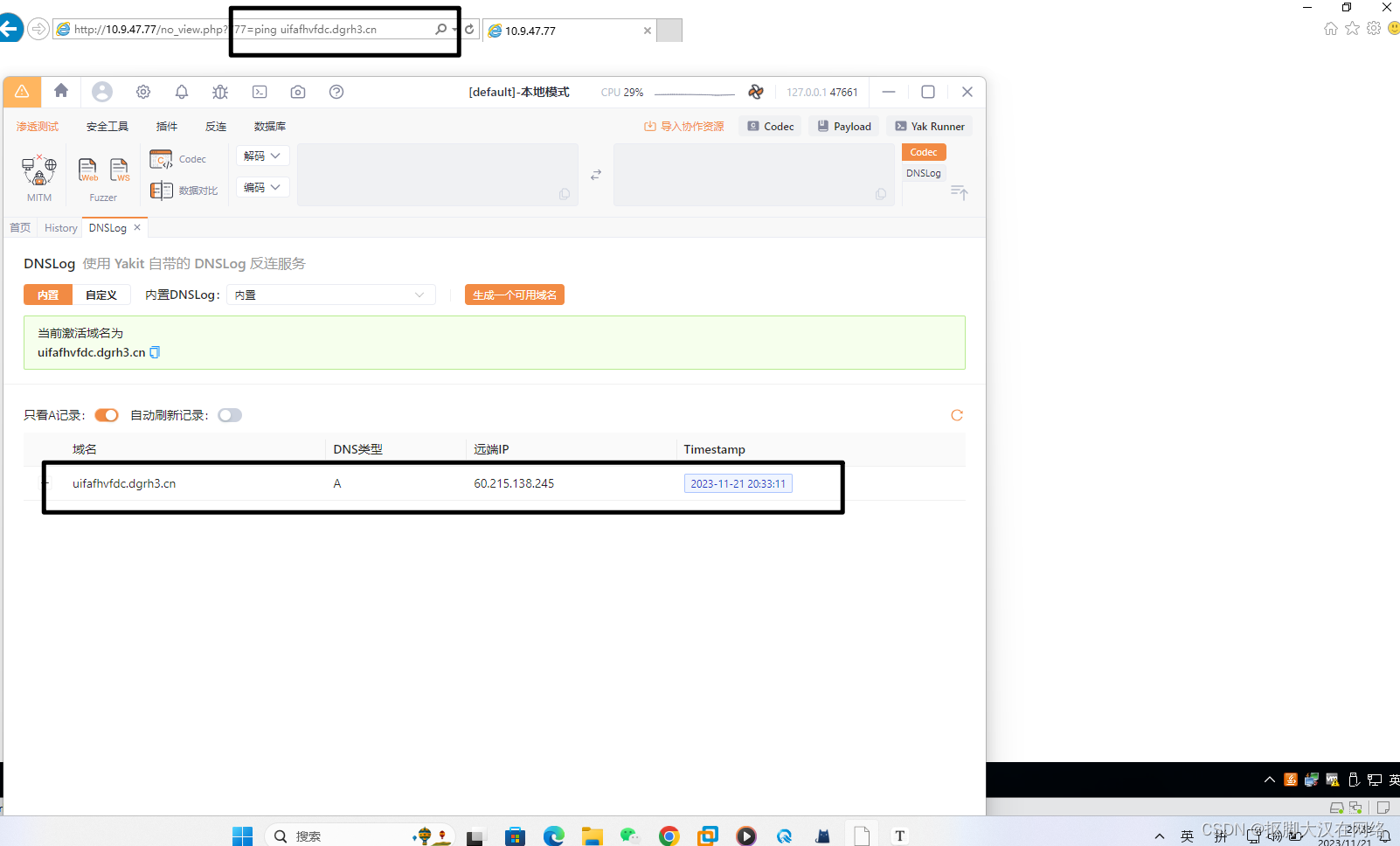
在无回显的情况下如何判断是否存在命令注入漏洞
news2026/2/15 14:55:47
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1234887.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
shell脚本判断语句
目录 一. 判断语句
1. 判断文件是否存在 test
2. 数值比较
3. 字符串比较
4. 逻辑运算
5. [ ] 与 [ [ ] ]
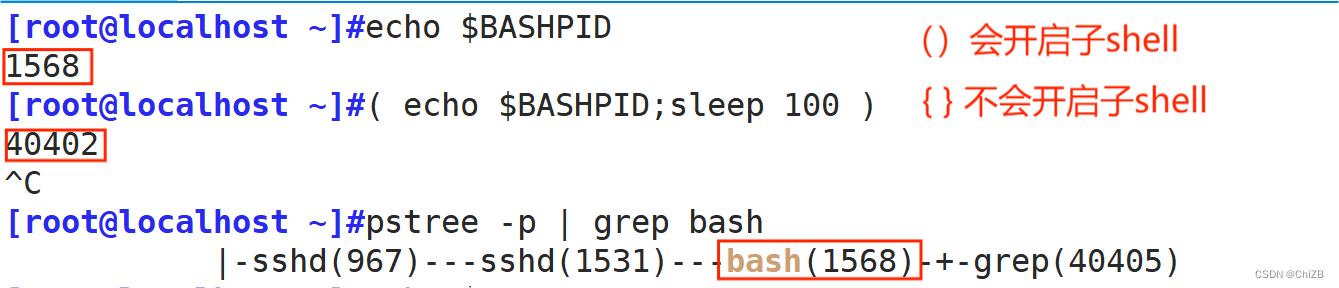
6. ( ) 与 { }
7. if 语句
二. 脚本应用 一. 判断语句
1. 判断文件是否存在 test 选项 -a 和 -e 都可以判断文件是否存在 只是 -a 选项在取反时有问题…
数字化转型导师坚鹏:数字化时代银行网点厅堂营销5大特点分析
数字化时代银行网点厅堂营销存在以下5大特点:
1、产品多样化:在数字化时代,银行的产品和服务变得更加多样化。除了传统的存款、贷款、理财等金融服务外,还新增了各种创新产品,如网上银行、移动支付、投资咨询、保险、…
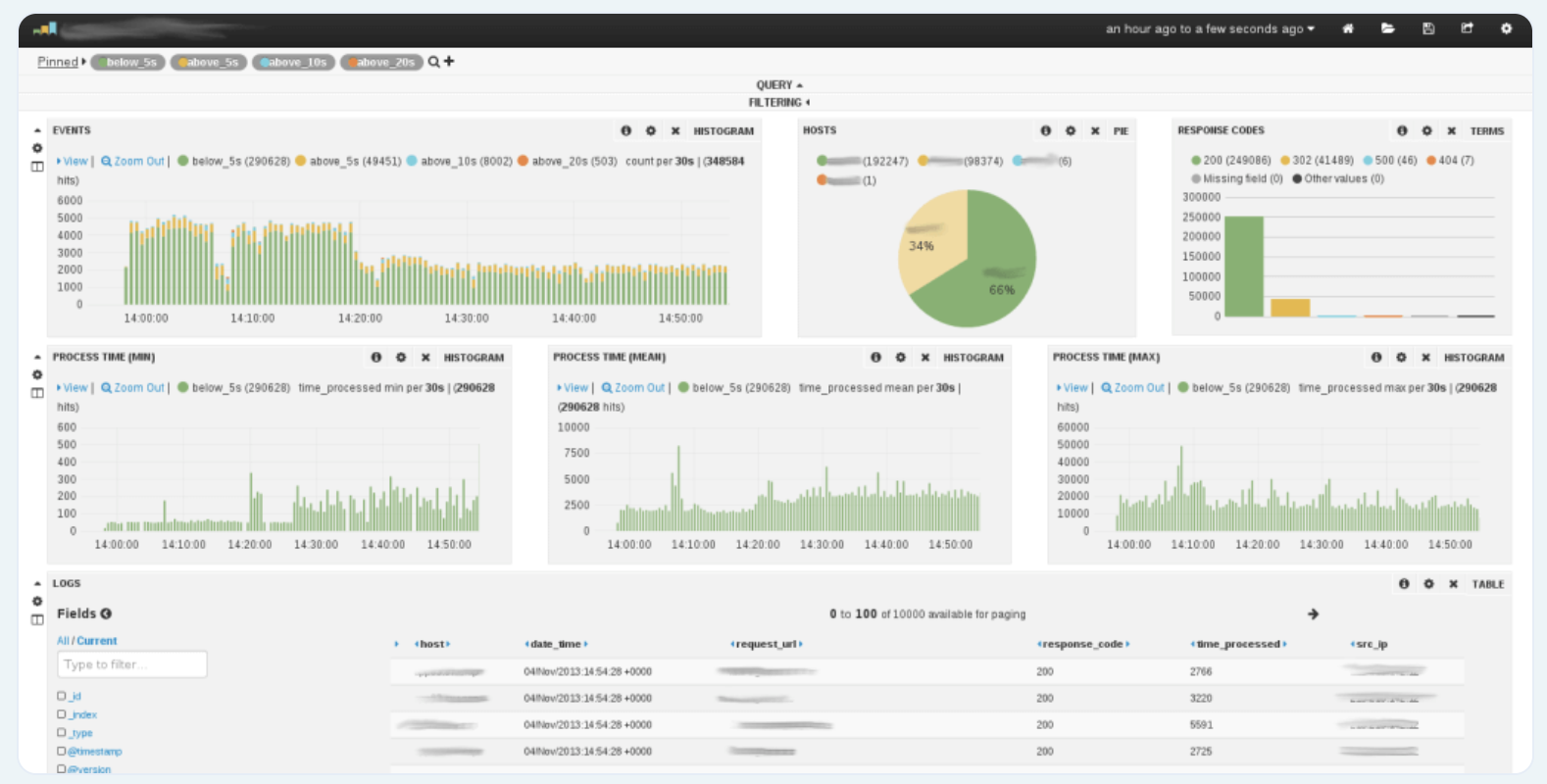
5 个适用于 Linux 的开源日志监控和管理工具
当Linux等操作系统运行时,会发生许多事件和在后台运行的进程,以实现系统资源的高效可靠的使用。这些事件可能发生在系统软件中,例如 init 或 systemd 进程或用户应用程序,例如 Apache、MySQL、FTP 等。 为了了解系统和不同应用程序…
离线安装Linux包的方法
sklearn库安装方法(有详细步骤流程) 离线安装Linux包的方法——以sklearn为例 https://pypi.org/project/scikit-learn
百度搜索万亿规模特征计算系统实践
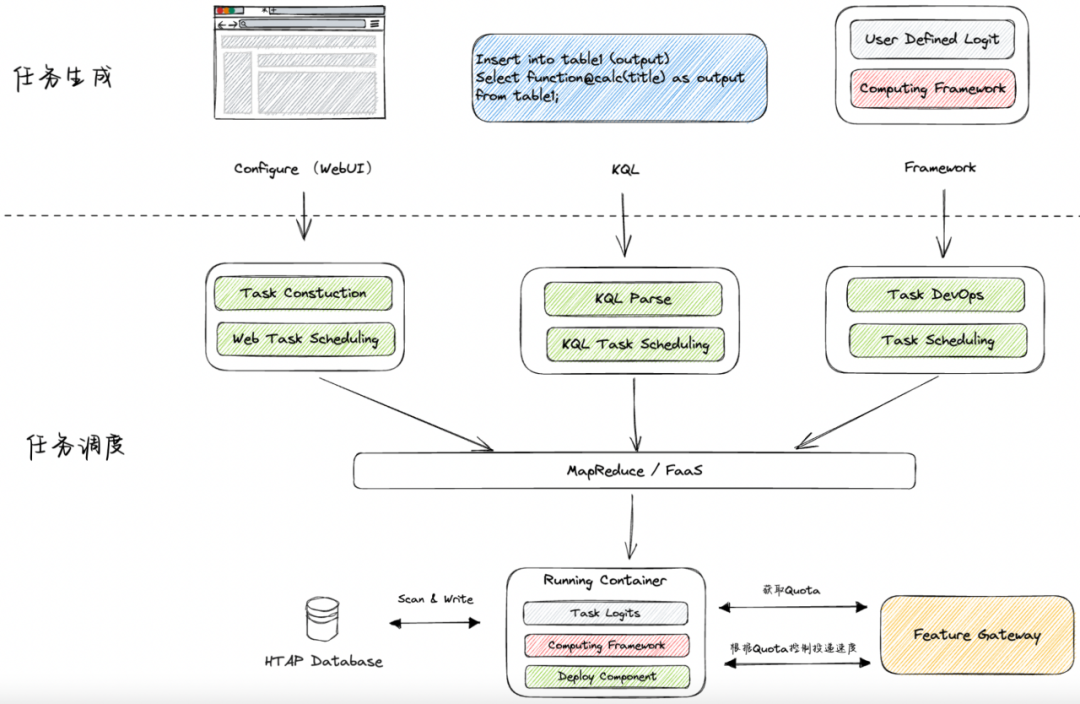
作者 | Jay 导读 本文主要介绍百度搜索在全网万亿级规模内容做内容理解的工程实践,涉及机器学习工程化、资源调度、存储优化等多个Topic。 全文6648字,预计阅读时间17分钟。 01 业务背景
百度收录了互联网海量内容,要索引这些内容࿰…
基于单片机预费电表控制系统(proteus仿真+源程序)
一、系统方案 1、本设计采用这51单片机作为主控器。 2、采集电量值送到液晶1602显示。 3、按键设置预设值,实际使用电量超过设置,蜂鸣器报警。
二、硬件设计 原理图如下:
三、单片机软件设计 1、首先是系统初始化 void LCD_init(void) { …
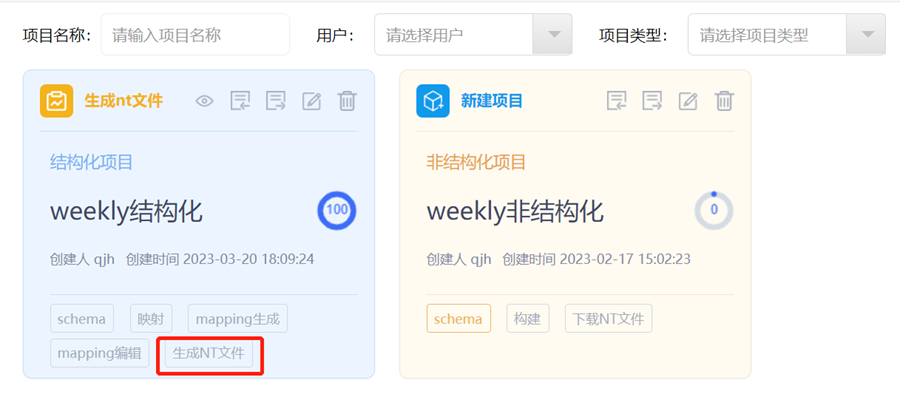
#gStore-weekly | gBuilder功能详解之结构化数据抽取
上一个weekly中已经详细讲解了schema的设计,在schema设计好了之后,gBuilder支持将结构化和非结构化数据转化为RDF图数据。其中结构化数据支持数据的无损转化。
1. 技术介绍
gBuilder的结构化数据抽取采用D2RQ技术实现。
DR2Q是一个能够将关系数据库中…
Redis从入门到精通(二)- 入门篇
文章目录 0. 前言1. 入门篇[【入门篇】1.1 redis 基础数据类型详解和示例](https://icepip.blog.csdn.net/article/details/134438573)[【入门篇】1.2 Redis 客户端之 Jedis 详解和示例](https://icepip.blog.csdn.net/article/details/134440061)[【入门篇】1.3 redis客户端之…
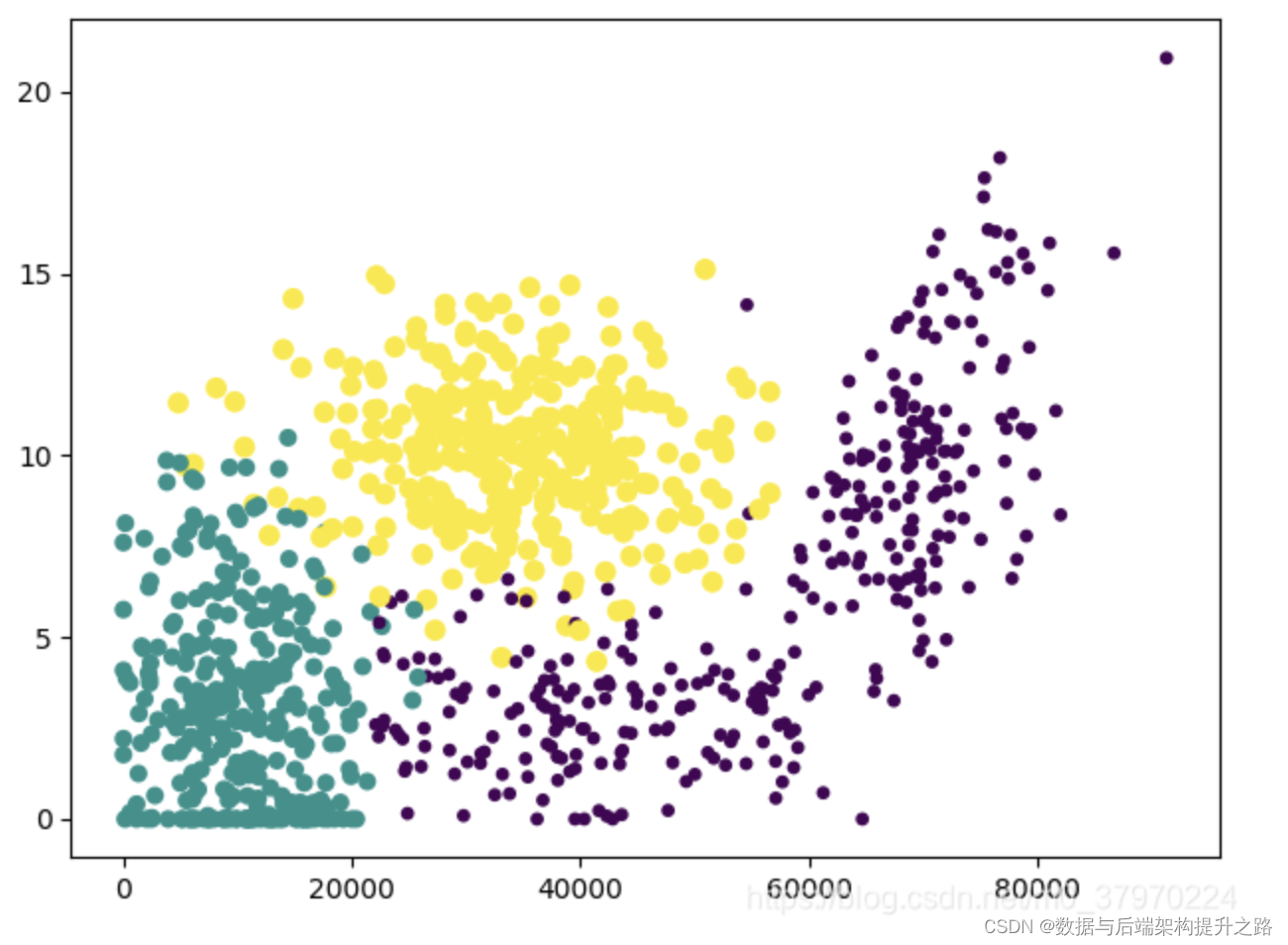
KNN(k近邻法)算法理论和实战
KNN概念
k近邻法(k-nearest neighbor,k-NN)是一种基本分类与回归方法。
k近邻法的输入为实例的特征向量对应于特征空间的点;输出为实例的类别,可以取多类。
k近邻法假设给定一个训练数据集,其中的实例类…
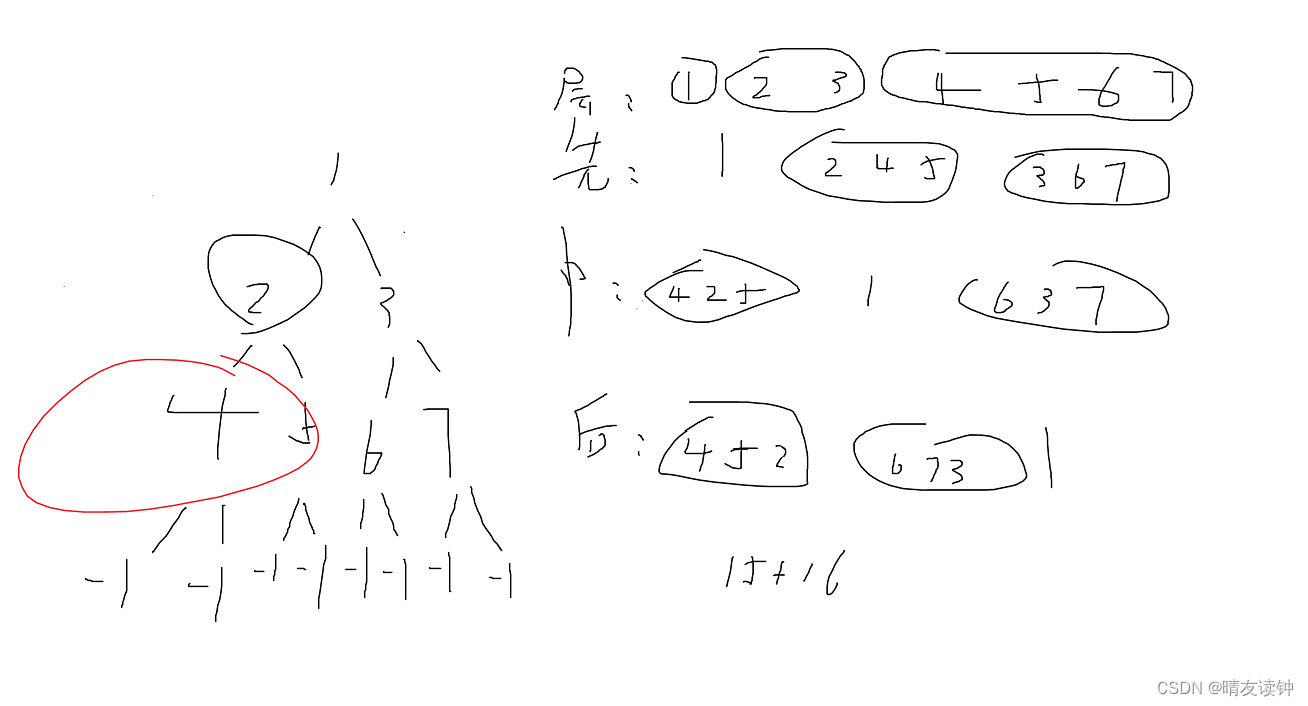
基于非链式(数组)结点结构的二叉树的层序、先序、中序、后序输入创建以及层序、先序、中序、后序输出
这个系列来记录学习一下如何用数组完成二叉树的4种顺序的创建,以及其4种顺序的遍历。
我们知道,对于一棵二叉树而言它有4种遍历的顺序,那自然就导致其输入结点时,也分这四种顺序。
分别是—— 层序: …
Kotlin 核心语法,为什么选择Kotlin ?
Kotlin 是一个基于 JVM 的新的编程语言,由 JetBrains 开发。与Java相比,Kotlin的语法更简洁、更具表达性,而且提供了更多的特性。
Kotlin是使用Java开发者的思维被创建的,Intellij作为它主要的开发IDE。对于 Android开发者&#…
Java实现围棋算法
围棋是一种源自中国的棋类游戏,也是世界上最古老、最复杂的棋类游戏之一。该游戏由黑白两方交替放置棋子在棋盘上进行,目的是将自己的棋子占据更多的空间,并将对手的棋子围死或吃掉,最终获得胜利。围棋不仅是一种游戏,…
两种Deformable Attention的区别
先分别写一下流程
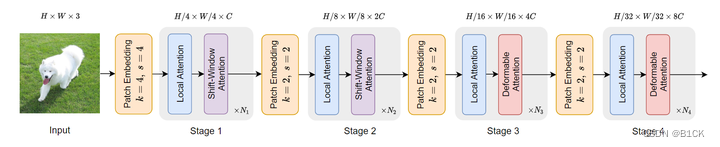
Deformable DETR(2020)的Deformable Attention 解释: Deformable Attention如下图所示K3, M3K是指每个zq会和K个offset算attention,M是指M个head, z q z_q zq有NHW个: 参考点:reference points&am…
golang学习笔记——接口和继承比较1
继承
Go 语言的设计之初,就不打算支持面向对象的编程特性,因此 Go 不支持面向对象的三大特性之一——继承。但是 Go 可以通过组合的思想去实现 “继承”。继承是面向对象的三大特性之一,继承是从已有的类中派生出新的类,新的类能…
快速幂极简写法快速幂求逆元
快速幂原理介绍 快速幂模板
int qmi(int a, int k, int p) {int res 1;while (k) {//后面的a其实是底数与其指数的运算结果了,是不断迭代的//第一个a其实就是a的2的0次方if (k & 1) res (res * a) % p;a (a * a) % p;//注意,a是一个不断变化的过…
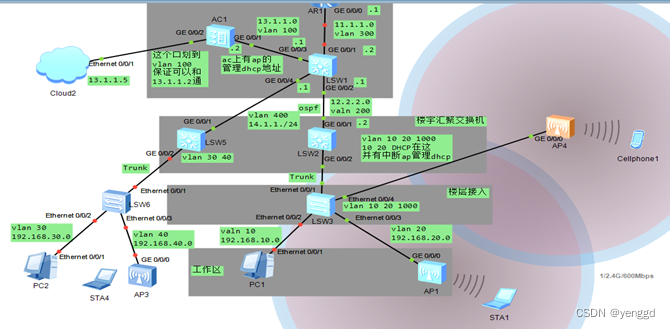
华为ac+fit无线2层漫游配置案例
ap的管理dhcp在ac上,业务dhcp在汇聚交换机上、并且带2层漫游
R1: interface GigabitEthernet0/0/0 ip address 11.1.1.1 255.255.255.0 ip route-static 12.2.2.0 255.255.255.0 11.1.1.2 ip route-static 192.168.0.0 255.255.0.0 11.1.1.2
lsw1: vlan batch 100…
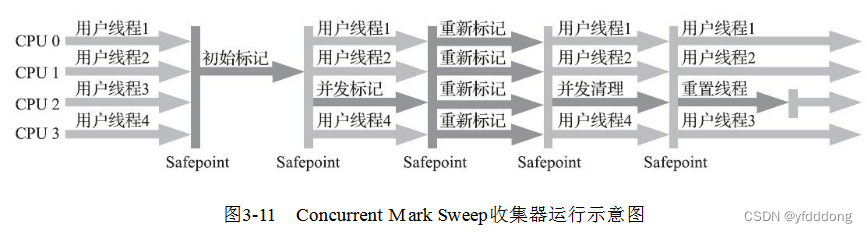
深入理解Java虚拟机-GC
深入理解Java虚拟机-GC
当需要排查各种内存溢出、内存泄漏时,当垃圾回收成为系统到达更高并发量的瓶颈时,我们必须对内存动态分配和内存回收技术这样的“自动化”技术采用必要的监控和调节。
Java堆和方法区:一个接口的多个实现类需要的内存…
基于知识问答的上下文学习中的代码风格11.20
基于知识问答的上下文学习中的代码风格 摘要1 引言2 相关工作3 方法3.1 概述3.2 元函数设计3.3 推理 4 实验4.1 实验设置4.2 实施细节4.3 主要结果 摘要
现有的基于知识的问题分类方法通常依赖于复杂的训练技术和模型框架,在实际应用中存在诸多局限性。最近&#x…