目录
1 我们本节主要介绍的
2 Minimum Snap Optimization
2.1 Differential Flatness(微分平坦)
2 Minimum Snap
3 Closed-form Solution to Minimum Snap
3.1 Decision variable mapping 待优化问题的映射
4 凸优化 及其它问题
1 我们本节主要介绍的
1.轨迹优化需要有边界条件(从当前运动开始的,起始状态-->终止状态)
2.中继节点:我希望经过中继点(到达一个路标点),当然,这个路标点也可以是我们中间的节点(通过路径搜索得到的)。
3.需要有评价函数:评价这个是光滑(经过路标点的左极限右极限)且是动力学可行的。
2 Minimum Snap Optimization
2.1 Differential Flatness(微分平坦)
数学模型描述:
- 无人机的状态(states)指的是位置、速度和朝向等物理量,而输入(inputs)通常是指施加在无人机上的控制信号,比如推力或转矩。
- 这段话表达了一种表示无人机状态和输入的方法:它们可以用代数函数来表达,而这些函数是关于四个特定的平面输出(flat outputs)及其导数的。
平面输出的作用:
- 通过选取这四个特定的输出以及它们的导数,可以更有效地描述无人机的状态和输入。这种选择有助于简化无人机运动的数学表达。
- 这种方法的好处之一是能够自动生成飞行路径(trajectories)。
路径生成和跟踪:
- 在平面输出的空间中,几乎任何光滑的路径都可以通过这种模型下的无人机来追踪。
- 这意味着,只要在平面输出的空间中给定了一个光滑的路径,这个无人机就可以按照这个路径飞行。
一个可能的选择:
- 这段话提到了一个可能的选择,即选取的四个平面输出分别是位置的 x、y、z 分量和朝向 ψ(通常表示偏航角度)。
- 平面输出空间中的轨迹(Trajectory)σ_t 是一个函数,将时间作为参数,输出无人机在三维空间中的位置和旋转。
我们先看无人机的状态:12维度
3维位置 + 3维无人机的转动姿态 + 3维xyz运动的速度 + 3个旋转姿态的角速度
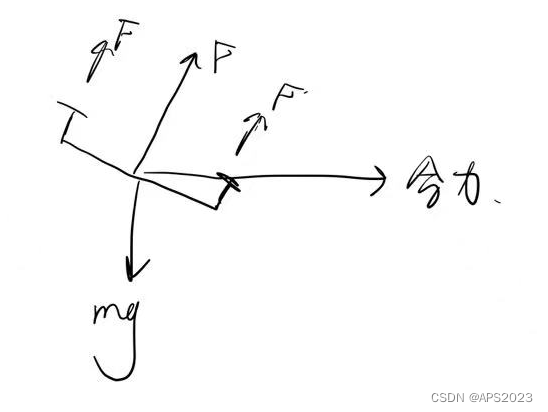
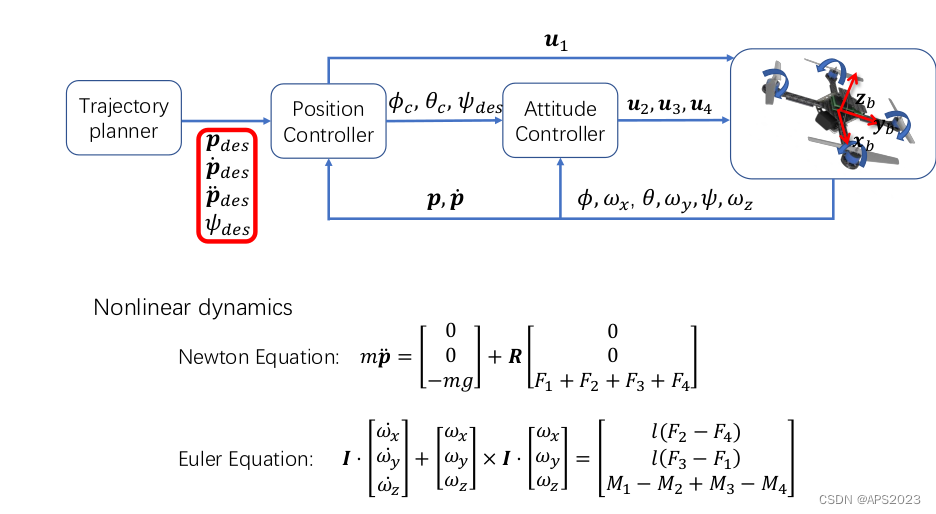
无人机飞行的运动方程:我们通过牛顿方程和欧拉方程描述
无人机的合力垂直于螺旋桨的,ma = -mg + R(F1+F2+F3+F4)就是一个牛顿第二定律,R是坐标变换。第二-四表示转动的关系表示力矩。
我们证明确实可以把无人机的12维状态量压缩到xyz、yaw上:
无人机做planing是否需要对姿态进行planing?它的姿态一定和它的加速度绑定在一起的,因为无人机的合推力一定垂直于螺旋桨的平面垂直于自己的body frame的Z轴产生的推力。我们来看一种情况:
无人机的合力方向是确定的,合力提供的加速度是知道的。
到此推导完毕。
2 Minimum Snap
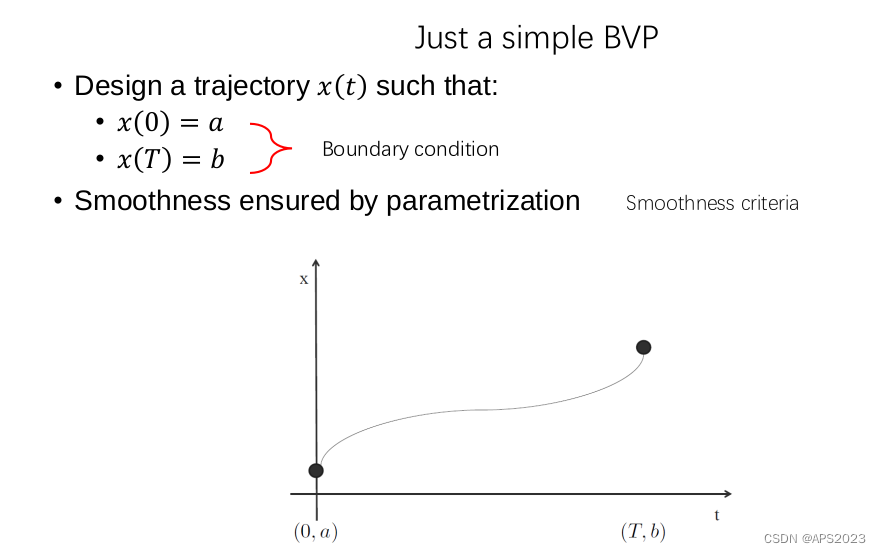
先拿一维来说,如果我们要生成一个光滑的一段轨迹:
光滑等价于可导。(多项式其实就是光滑的,多阶微分可导)(如果要求速度连续,则加速度可导)
连续要保证左右极限相同。
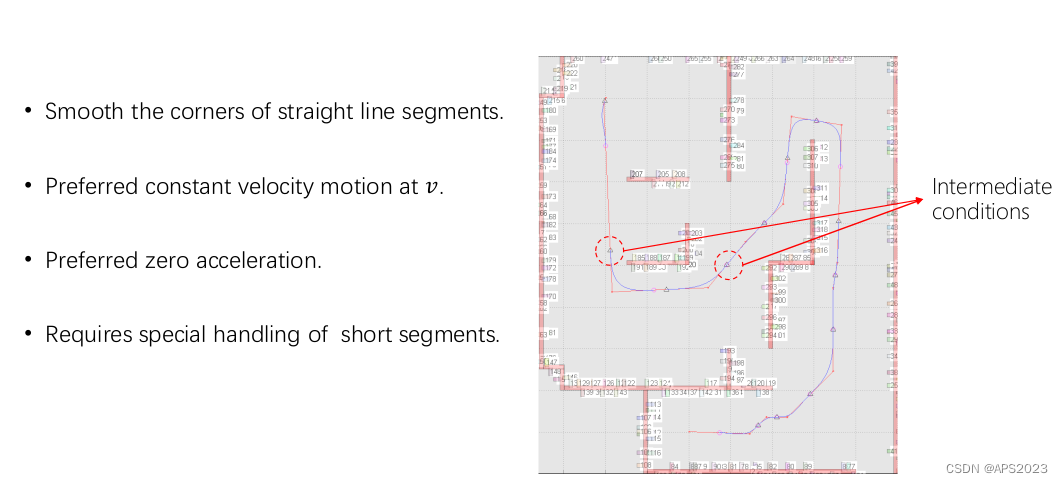
如果多段呢?
我们假设每一段有一个多项式函数,我们的机器人要通过中间点,要给定一个速度加速度的值如下:
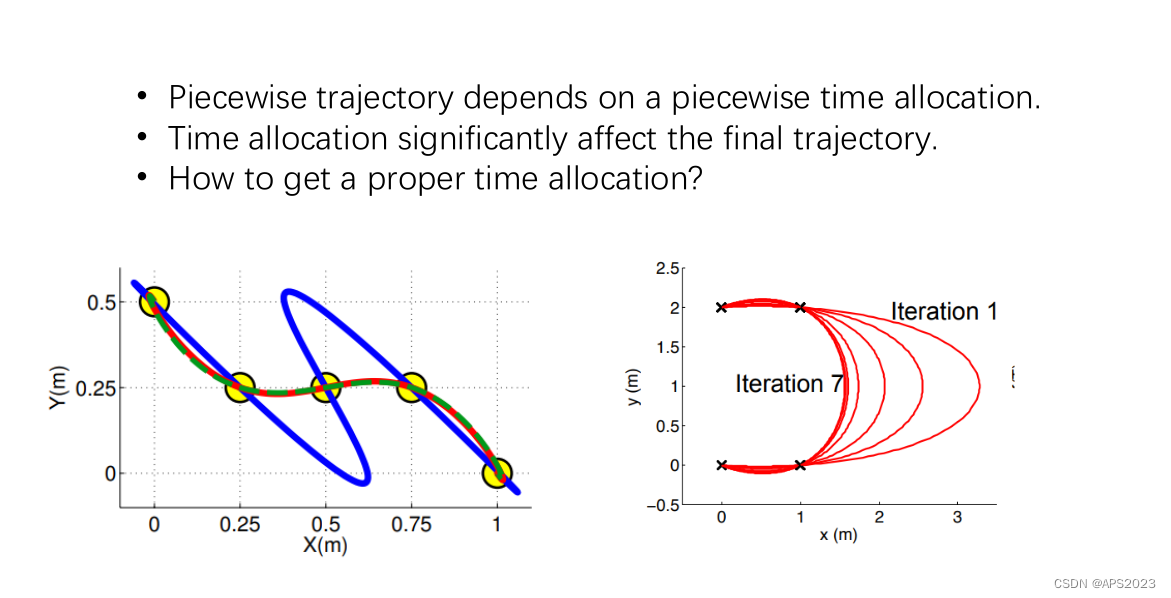
但是中间节点的速度,加速度是我们人为指定的,指定多少是合理的呢?我们往往是指定不了的,我们要去利用优化的思想去求解!
那么我们现在的目标就是求解多段多项式:
满足首末约束,经过中间点,中间点的左右极限高阶导数相同(光滑连续),整体轨迹snap最小。
我们可以看一下分段多项式的形式:
每一段轨迹都是多项式、每一段轨迹的时间一定要是已知的。
那么我们怎么合理的选择轨迹的阶数呢?
1.确保轨迹连续性
2.确保轨迹的光滑性
3.确保优化阶数最小
工程上我们有些约定:
如果我们的轨迹是K段的,我们最小化jerk,首位各提供三个约束(P、V、A),中间有K-1个分段点。每个点提供了位置约束(K-1个P约束),总共有 3 + 3 + K - 1 = K + 5个约束
有K段轨迹,每段的阶数为N,每一段轨迹提供的未知数的自由度是N+1,总共是(N+1)*K,因此可以算出最低的N。
还有时间线的问题:
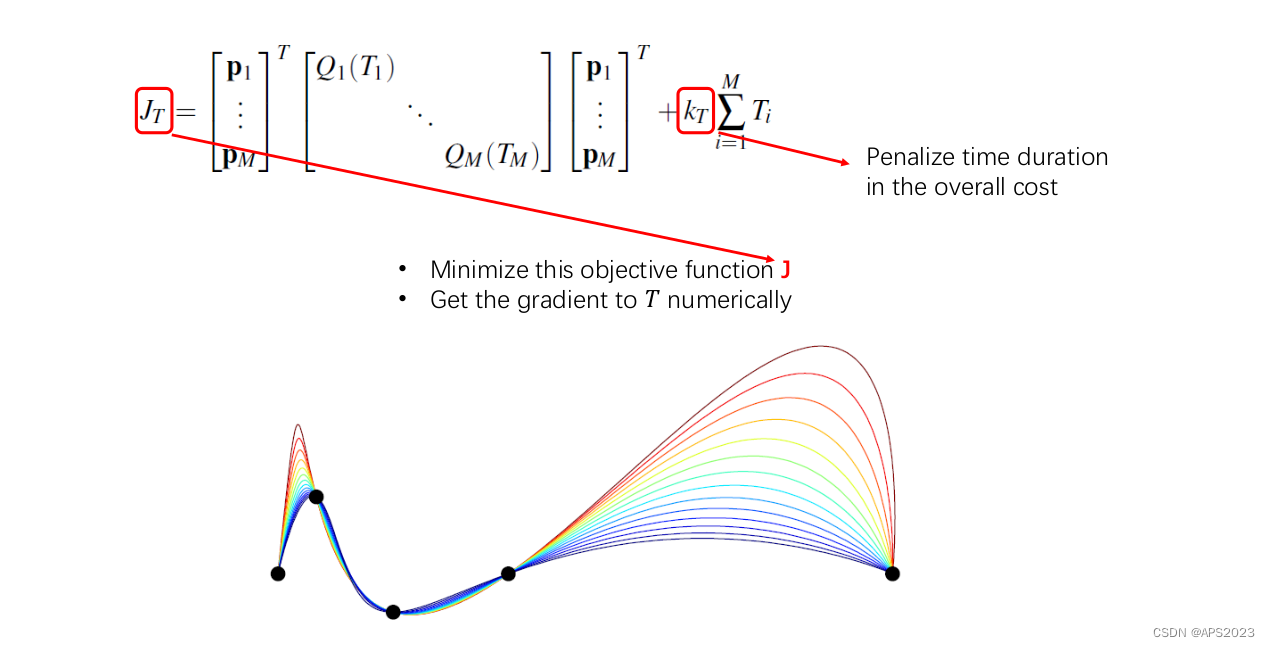
我们来计算代价函数:
Qj是海森矩阵。
我们要对优化问题增加一些约束:
这是一个等式约束,同样的我们要增加连续性约束:
是一个凸优化的问题:
是考研数学的内容:凸集合就是我们在集合中取到任意两个点连接这条线上的每两个点都在集合中:
那什么是凸优化问题呢?
我们有一个目标函数
,它会受制于一些不等式、等式约束。
几种优化问题:
3 Closed-form Solution to Minimum Snap
3.1 Decision variable mapping 待优化问题的映射
我们之前明白了我们优化的其实是多项式的系数:五阶的话就是
,这样的话其实会问题,这里我们求解出了
其实是没有物理含义的。如果我们求解一个
非常大,那么就会出现轨迹不稳定的问题。因此中间点的va需要根据物理意义去求最优解。
那么我们怎么做?我们需要构造映射矩阵M,把所有我们要求解的p映射为端点的导数。
那应该怎么写呢?把多项式的系数映射成导数。
d怎么排布呢?端点的导数,和p排列对应,那么d就是排布第一个点的各阶导数、第二个点的各阶导数......
上面是推导。
我们通过两个式子可以得到下面的式子:
将固定不变的变量和优化变量进行分解:
构造选择矩阵
,乘以构造的结果等于原来端点的导数:df固定的变量、dp待优化变量。
我们求到了解析解
。
我们来看看如何写这个
:
第i段轨迹的最前面的点和最后面的点的各阶导数。我们有16个的量、但是有4个重叠的量,因此只有12个。
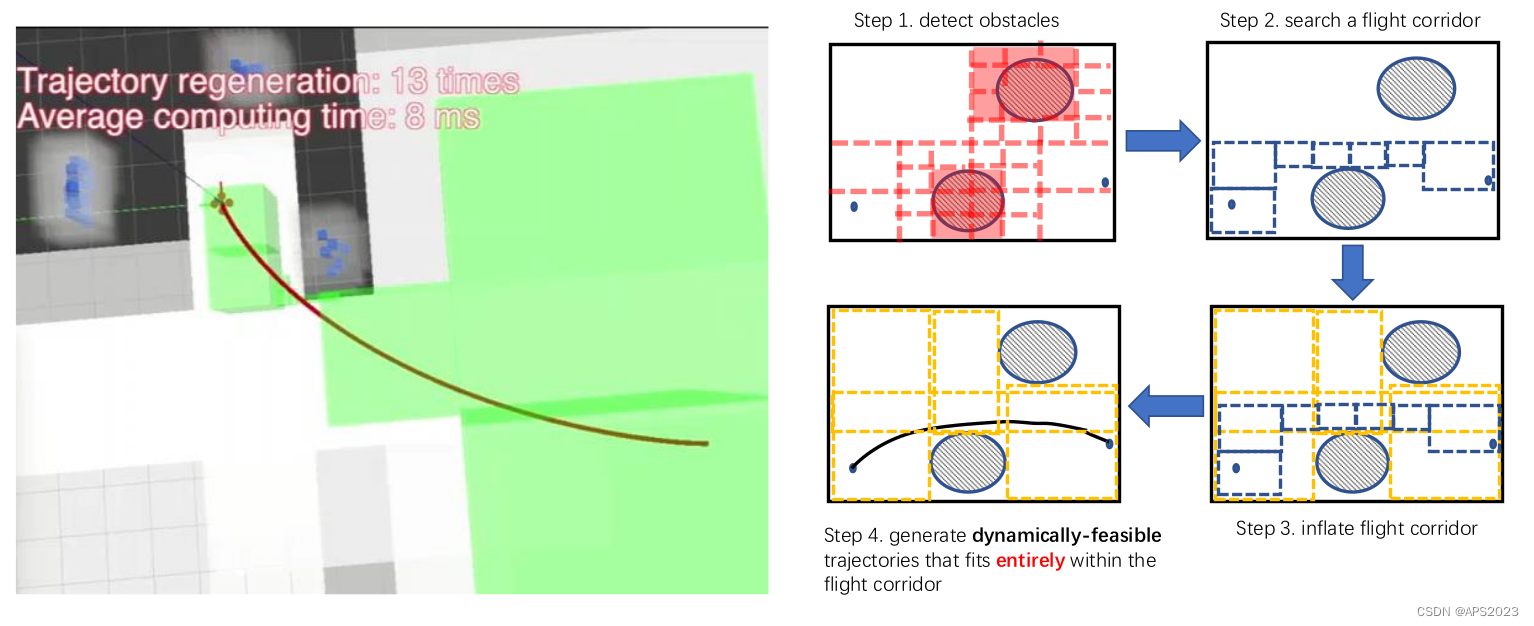
安全性呢?生成轨迹的时候可能撞车??
如果我们碰到了障碍物,我们在轨迹的中间新生成一个路标点去新生成轨迹。
但这也不是很好的:我们添加不等式约束
4 凸优化 及其它问题
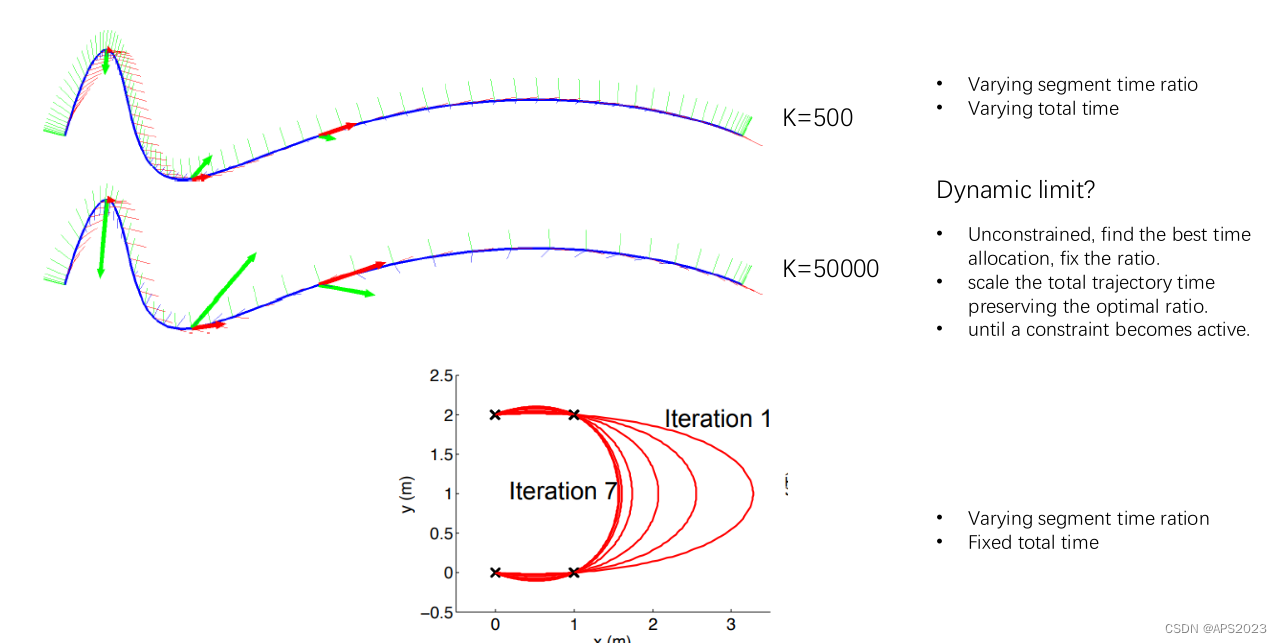
Numerical Stability:数值稳定性












































![2023年中国羽绒制品需求现状、市场规模及细分产品规模分析[图]](https://img-blog.csdnimg.cn/img_convert/2c5266ceeb3caa72909d677679b46acd.png)