照片由 丹·克里斯蒂安·佩杜雷什 on Unsplash
一、说明
在本文中,我们将探讨希尔伯特空间这个非常重要的主题。希尔伯特空间由于其特性而经常出现在物理和工程中。为了理解希尔伯特空间,我们从度量空间的定义开始。
二、基础概念
集合是定义明确的元素的集合。虽然集合本身可能不是很有用,但它们提供了一个非常强大的框架,可以通过笛卡尔积等操作系统地研究更复杂的对象。集合通常使用大写字母表示。
2.1 什么是度量空间
考虑一个任意非空集合 M。定义具有以下属性的操作 d:
- d(x,y) 是一个实数。从形式上讲,d 是一个 Mapping:
![]()
- 非负性质:d(x,y) ≥ 0
- d(x,y) = 0 iff x=y
- 对称性:d(x,y) = d(y,x)
- 三角不等式 d(x,y) ≤ d(x,z)+d(z,y)
其中 x、y 和 z 是 M 的元素。配备有这种运算 d 的集合 M 称为度量空间,表示为 (M,d)。
d 有时被称为距离。
应该注意的是,M 本身不是一个度量空间,因为 d 必须单独定义。
示例:考虑实数 R 的集合。 d₁ 和 d₂ 都是有效的指标。 d₂ 可能看起来很奇怪,但仍然有效。
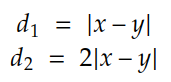
通常,指标是从上下文中理解的,例如实数集。
自定义指标的常见示例是机器学习算法(如 K 最近邻)中使用的距离度量。
2.2 完整的空间
度量空间中的序列 xn 是从自然数集到度量空间 X 元素的映射。也就是说,它是属于 X 的元素的有序序列。
柯西序列是元素在度量意义上不断靠拢的序列 d。从形式上讲,每个 r > 0 都存在一些 N,因此:
![]()
如果在 (X, d) 上定义的每个柯西序列 xn 收敛到 (X, d) 中的元素,则度量空间 (X, d) 是完整的。也就是说,取 (X, d) 上柯西的所有可能序列,如果它们最终收敛到 (X, d) 中的元素,则它是一个完整的空间。
2.3 不完整空间示例
考虑 Rational Numbers 的度量空间,其中度量为 |x-y|。柯西序列

收敛到 e,它不是 X 的元素。因此,有理数序列x【n】不是完备序列,就是说,序列x【n】从有理数集合虽然有极限,但极限不在有理数集合范围内。
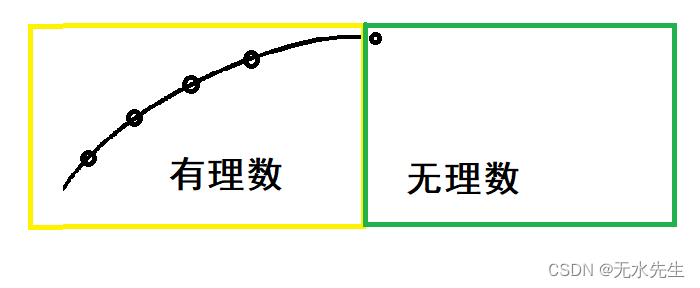
如图表示不完备性:就是有理数中的一个数列,按某个运算法则,其结果从有道理集合跑到集合之外。这种现象称为不完备。
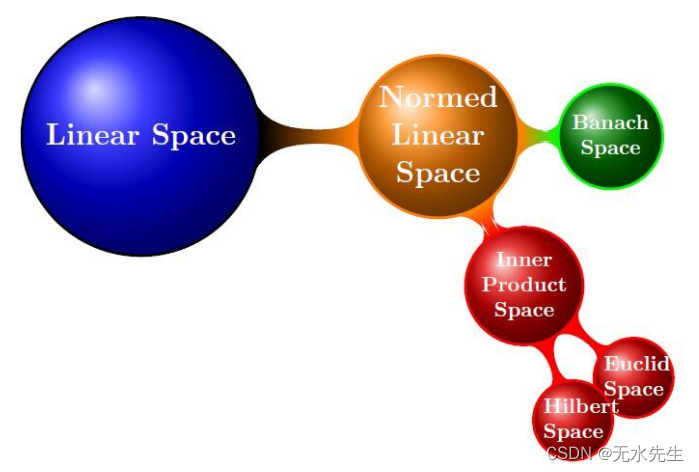
三、线性空间
标量 Field 上的线性空间 V 是定义加法和标量乘法运算的集合。总结一下:
- 元素添加是交换的和关联的。
- 两个加法都存在一个恒等元素 O。
- 存在加法逆。
- 标量乘法是加法的、分配的和关联的。
请注意,在工程和物理中,矢量空间和线性空间是同义词。有关属性的更好说明,请参阅此链接。
请注意,字段是定义了 +、* 的代数结构。
3.1 规范线性空间
规范 ||.||线性空间 V 是一个函数,它将集合的元素映射到具有以下属性的实数:
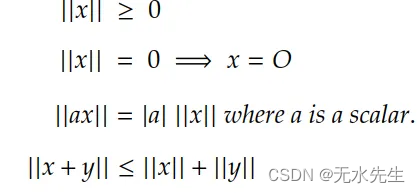
其中 x 是 V 的一个元素。配备范数的线性空间称为范数线性空间。由于函数 ||x-y||满足度量的属性,它是规范线性空间的自然度量。也就是说,规范线性空间始终是度量空间。当然,其他指标也可能是可能的。
范数是一种量级。
3.2 巴纳赫空间
如果度量 || 的范数线性空间 (X, ||.||) 是完整的x-y||,则称为 Banach 空间。
现在,我们可以定义希尔伯特空间。
四、内积空间
给定线性空间 X,内积 <x,y> 是具有以下属性的运算:
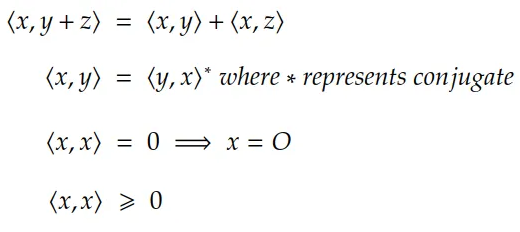
其中 x、y 和 z 是 X 的元素。具有定义内积的线性空间称为内积空间。请注意,内部产品空间的可能规范是:
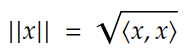
因此,每个内积空间也是一个规范线性空间。
五、希尔伯特空间
下标完备的内积空间:
![]()
被称为希尔伯特空间。
在数学里,希尔伯特空间(英语:Hilbert space)即完备的内积空间,也就是一个带有内积的完备向量空间。内积的构造推广了欧几里得空间的距离和角的概念;完备则确保了其上所有的柯西序列会收敛到此空间里的一点,从而微积分中的许多概念都可以推广到希尔伯特空间中。
希尔伯特空间为基于任意正交系上的多项式表示的傅立叶级数和傅立叶变换提供了一种有效的表述方式,而这也是泛函分析的核心概念之一。另外希尔伯特空间也是量子力学的重要数学基础之一。