树，二叉树，二叉树遍历，哈夫曼树（详解+刷题）

👂 后街男孩经典之精选 - 歌单 - 网易云音乐

👂 年轮（电视剧《花千骨》男声版插曲） - 汪苏泷 - 单曲 - 网易云音乐

🌼5.1 -- 树

🌼5.2 -- 二叉树

1，性质

2，存储

3，创建

🌼5.3 -- 二叉树遍历

(1)先序

(2)中序

(3)后续

(4)层序

(5)还原树

⚽刷题

🦎P1305 新二叉树

🦎Tree Recovery

🦎Tree

🌼5.4 -- 哈夫曼树

1，前置知识

2，实现

3，分析

4，优化

⚽刷题

🦎围栏修复

🦎信息熵

🦎转换哈夫曼编码

🌼5.1 -- 树

1，树：除根节点，分为 m 个互不相交的有限集

2，节点的度：节点拥有的子树个数

3，由于树中没有环，树中任意两个节点的路径是唯一的

4，有序树：节点的各子树，从左至右有序，不能互换位置

5，树 -- 顺序存储 -- 3种方式👇

#图解数据结构：树的存储结构 - 知乎 (zhihu.com)

双亲表示法，无法直接得到该节点的孩子；孩子表示法，由于不知道每个节点到底有多少个孩子，只能按照树的度（节点的最大度）分配孩子空间，极大浪费空间；双亲孩子表示法，浪费空间

6，树 -- 链式存储 -- 2种方式

二叉树的链式存储 - C语言学习教程_C语言程序_ c语言编程_ c语言入门 (itheima.net)

（1）孩子链表表示法：

类似邻接表，表头包含数据元素data和指向第一个孩子的指针，所有孩子都放入一个单链表中，单链表中的节点记录该节点的下标和下一个节点的地址。

（2）孩子兄弟表示法：

类似二叉链表，节点存储数据域data和2个指针域（lchild和rchild），lchild存储第1个孩子地址，rchild存储右兄弟地址。

7，树，森林和二叉树的转换

（1）森林和二叉树（2）树和二叉树

森林、树与二叉树相互转换-阿里云开发者社区 (aliyun.com)

兄弟关系在右斜线上，长子是左孩子👆

8，总结

由于在普通的树中，每个节点子树个数不同，存储和运算都比较困难

（比如：不知道每个节点有多少个孩子，或者，知道用书中节点最大度分配空间，造成浪费）

因此实际应用中，将树 / 森林转换为二叉树（进行存储和运算）

二者存在唯一对应关系，不影响结果

🌼5.2 -- 二叉树

1，性质

（1）二叉树第 i 层至多有 $2^{i+1}$ 个节点（某一层）

（2）深度为 k 的二叉树至多有 $2^{k} - 1$ 个节点（总共）

（3）任何一棵二叉树，叶子数 $n_{0}^{}$ ，度为2的节点数 $n_{2}^{}$ ，那么 $n_{2}^{}$ $+ 1 =$ $n_{0}^{}$

-- 度表示节点拥有的子树个数 --

（4）具有 n 个节点的完全二叉树，深度为 $\left \lfloor \log n \right \rfloor + 1$

（5）完全二叉树，若从上至下，从左至右编号，编号为 i 的节点，其左孩子编号为 2*i，右孩子编号为 2*i + 1，双亲编号为 i / 2（下取整）

2，存储

完全二叉树 -- 顺序存储👇

二叉树的顺序存储结构（看了无师自通） (biancheng.net)

普通二叉树 -- 链式存储

（顺序存储需要补充为完全二叉树（补0），浪费空间）

链式存储分为二叉链表和三叉链表👇

二叉树的存储结构二叉链表三叉链表 - papering - 博客园 (cnblogs.com)

3，创建

树的应用 —— 二叉树的创建_创建二叉树_Ding Jiaxiong的博客-CSDN博客

👆就是《算法训练营入门篇》的原文，下面是代码👇

1，询问法

先序遍历顺序，每次输入节点信息后，都询问是否创建该节点的左 / 右子树（递归创建）

不创建则置空（NULL）

void createtree(Btree &T) //创建二叉树（询问法）
{
    char check; //是否创建左右孩子
    T = new Bnode;
    cout<<"请输入节点信息："<<endl; //输入根节点数据
    cin>>T->data;

    cout<<"是否添加 "<<T->data<<"的左孩子? (Y/N)"<<endl; //询问创建T的左子树
    cin>>check;
    if(check == "Y")
        createtree(T->lchild);
    else
        T->lchild = NULL;

    cout<<"是否添加 "<<T->data<<"的右孩子? (Y/N)"<<endl; //询问创建T的右子树
    cin>>check;
    if(check == "Y")
        createtree(T->rchild);
    else
        T->rchild = NULL;
}

2，补空法

为空则用特殊字符补空（比如"#"），依然是先序遍历和递归创建

void Createtree(Btree &T) //创建二叉树（补空）
{
    char ch;
    cin>>ch; //二叉树补空后，先序遍历输入字符
    if(ch == '#')
        T = NULL; //建空树
    else {
        T = new Bnode;
        T->data = ch; //生成根节点
        Createtree(T->lchild); //递归创建左子树
        Createtree(T->rchild); //递归创建右子树
    }
}

🌼5.3 -- 二叉树遍历

(1)先序

访问根，先序遍历左子树，左子树为空（或已遍历）才可以先序遍历右子树

void preorder(Btree T) //先序遍历
{
    if(T) {
        cout<<T->data<<" ";
        preorder(T->lchild);
        preorder(t->rchild);
    }
}

(2)中序

中序遍历左子树，左子树为空才可以访问根，最后中序遍历右子树

void inorder(Btree T) //中序遍历
{
    if(T) { //该节点不为空
        inorder(T->lchild); //中序遍历左子树
        cout<<T->data<<" "; //访问根节点
        inorder(t->rchild); //中序遍历右子树
    }
}

(3)后续

后续遍历左子树，后续遍历右子树，左右子树为空才可以先访问根

void posorder(Btree T) //后序遍历
{
    if(T) { //该节点不为空
        posorder(T->lchild); //后序遍历左子树
        posorder(t->rchild); //后序遍历右子树
        cout<<T->data<<" "; //访问根节点
    }
}

(4)层序

第1层开始，从左至右顺序访问（队列实现：先被访问节点的孩子也先被访问）

bool Leveltraverse(Btree T)
{
    Btree p;
    if(!T) 
        return false;
    queue<Btree>Q; //创建一个普通队列，存放指针类型
    Q.push(T); //根指针入队
    while(!Q.empty()) { //队列不为空
        p = Q.front(); //取队头作为当前节点
        Q.pop(); //队头出队
        cout<<p->data<<" ";
        if(p->lchild)
            Q.push(p->lchild); //左孩子指针入队
        if(p->rchild)
            Q.push(p->rchild); //右孩子指针入队
    }
    return true;
}

(5)还原树

根据遍历顺序，可以还原这棵树，包括二叉树还原，树还原，森林还原（3种方式）

1，二叉树还原

（已知中序和先序）

根据中序和先序或者中序和后续，可以唯一地还原二叉树

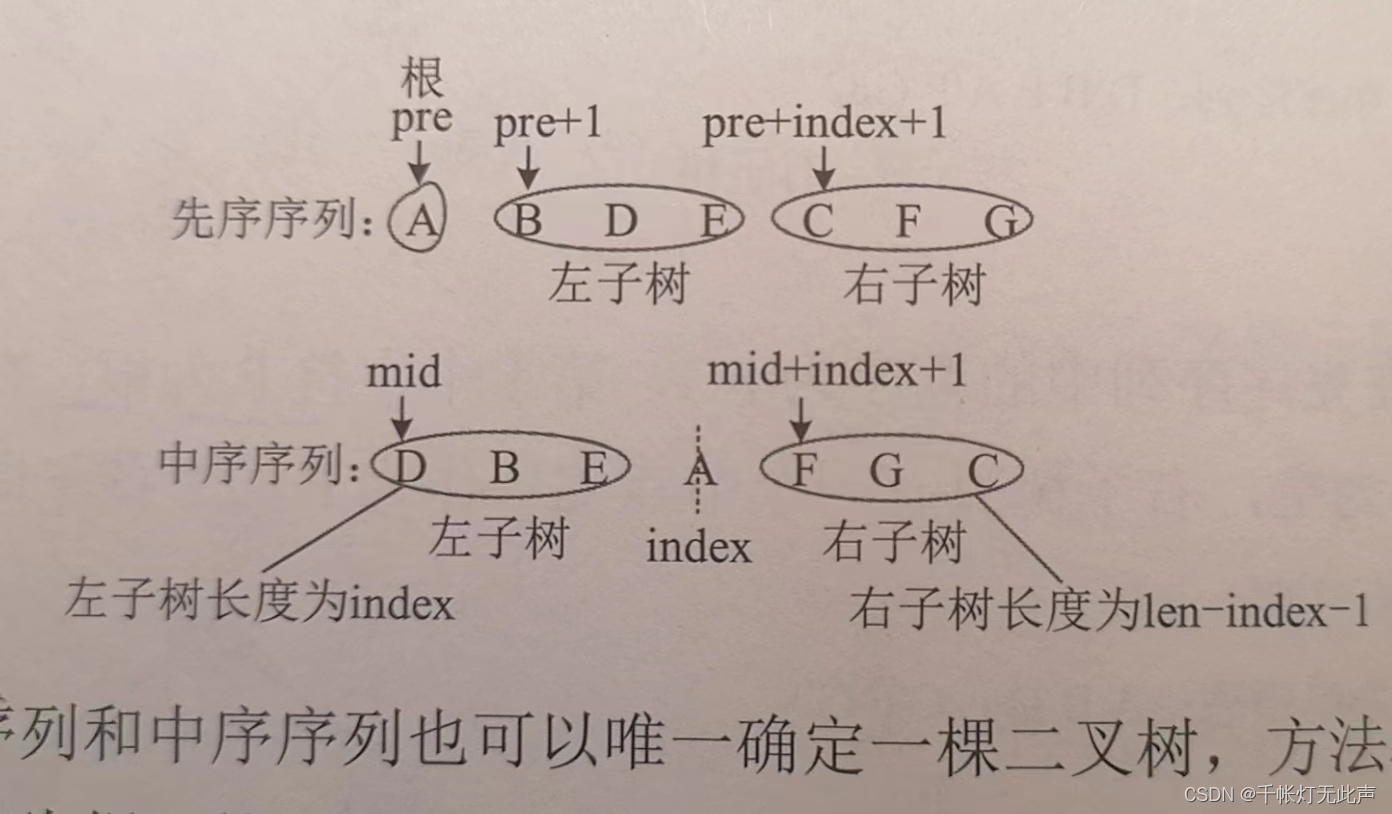
步骤：a.先序序列第1个字符为根 b.中序序列，以根为中心划分左右子树 c.重复上述步骤

eg:

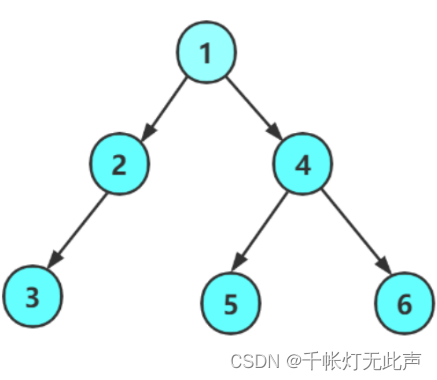
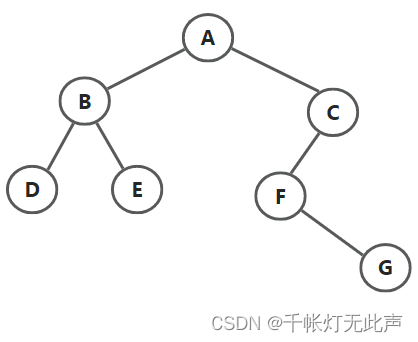
1，已知一棵二叉树，先序ABDECFG，中序DBEAFGC，那么根为A，左子树DBE，右子树FGC

分析1：

左子树DBE在先序中是BDE，所以左子树的根为B，且中序以B为中心划分左右孩子D，E

分析2：

右子树FGC在先序中是CFG，所以右子树的根为C，左子树包含FG，右子树空，先序中为FG，所以F为根，中序中以F为根划分左右子树，左子树为空，右子树为G

代码

BiTree pre_mid_createBiTree(char *pre, char *mid, int len) //先，中序还原二叉树
{
    if(len == 0)
        return NULL;
    char ch = pre[0]; //先序第1个节点，作为根
    int index = 0; //中序查找根节点，index记录查找长度
    while(mid[index] != ch)
        index++; //找到根节点后，左边左子树，右边右子树
    BiTree T = new BiTNode; //创建根节点
    T->data = ch;
    //递归创建左子树
    T->lchild = pre_mid_createBiTree(pre + 1, mid, index); 
    //递归创建右子树
    T->rchild = pre_mid_createBiTree(pre+index+1, mid+index+1, len-index-1); 
    return T;
}

👆代码解释👇

1，pre，mid为指针类型，分别指向先序，中序序列的首地址

len为序列长度

2，先序序列第1个字符pre[0]为根，index记录中序中查找pre[0]的长度

3，左子树：先序的首地址为pre + 1，中序首地址mid，长度index

4，右子树：先序首地址pre + index + 1，中序首地址mid + index + 1，长度len - index - 1

（右子树长度 = 总长度 - 左子树长度 - 根）

（已知中序和后序）

后序 DEBGFCA，中序 DBEAFGC

建议画图

BiTree pro_mid_createBiTree(char *last, char *mid, int len) //后中序建立二叉树
{
    if(len == 0)
        return NULL;
    char ch = last[len - 1]; //后续最后1个节点为根
    int index = 0; //中序查找根节点，index记录查找长度
    while(mid[index] != ch)
        index++;
    BiTree T = new BiTNode; //创建根节点
    T->data = ch;
    T->lchild = pro_mid_createBiTree(last, mid, index); //创建左子树
    T->rchild = pro_mid_createBiTree(last+index, mid+index+1, len-index-1); //创建右子树
    return T;
}

2，树还原

树的先序，中序遍历 == 二叉树的先序，中序遍历，所以

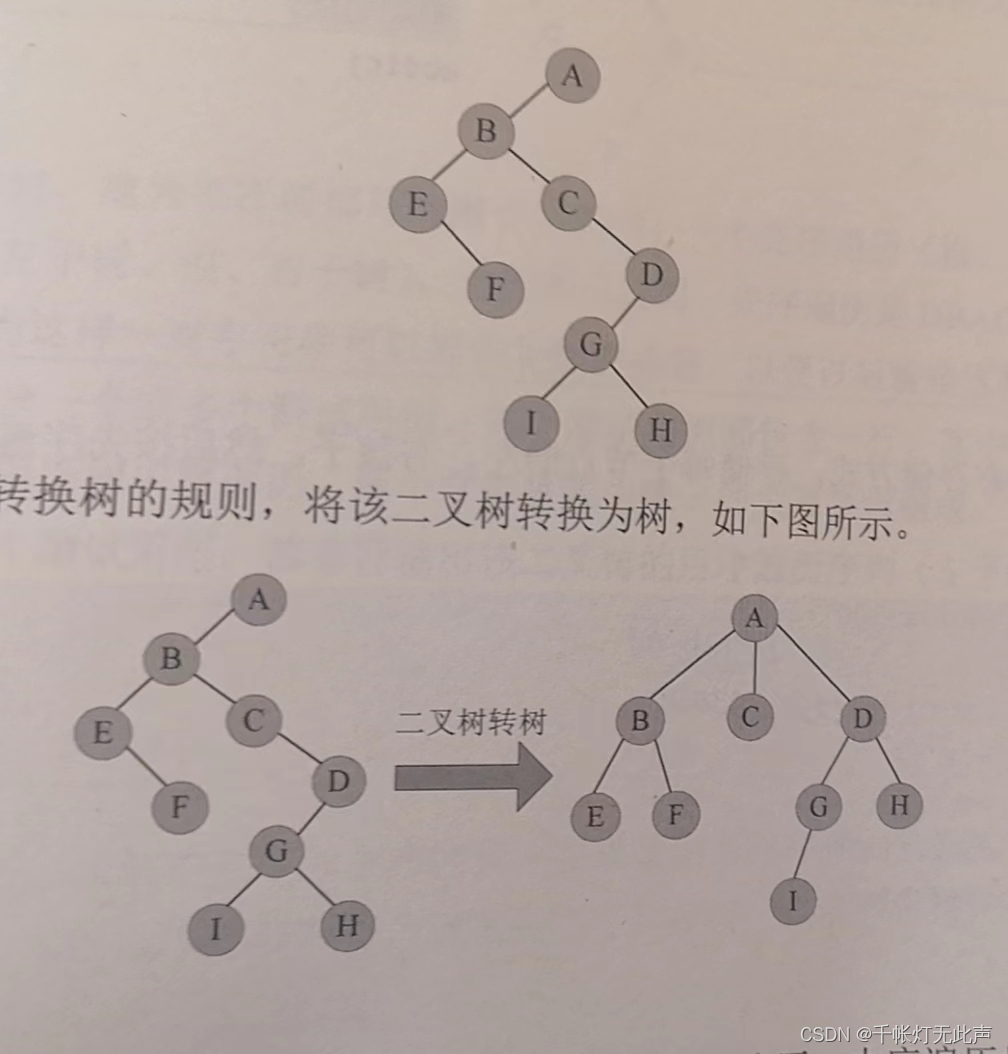
（根据给定的先序，中序序列）👇先还原为二叉树，再从二叉树转树

先序ABEFCDGIH，中序EFBCIGHDA （A是根）

先序BEFCDGIH，中序EFBCIGHD （B是根）

先序EFCDGIH，中序 (左)EF (右)CIGHD （E，C是根）

先序DGIH，中序IGHD （D是根）

先序GIH，中序IGH （G是根）

-->（至此，还原完毕）

👆二叉树转树，长子作为左孩子，兄弟关系右斜

3，森林还原

类似上面的树还原，区别在于，森林加1个根节点，就变成了普通的树

⚽刷题

🦎P1305 新二叉树

P1305 新二叉树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

静态存储的方式，l[]存储左儿子，r[]存储右儿子，比如：

l[0] == 1表示a的左儿子是b

r[0] == 2表示a的右儿子是c

#include<iostream>
using namespace std;

int l[30], r[30], root, n;
string s;

void preorder(int t) //先序遍历
{
    if(t != '*' - 'a') { //非空节点
        cout<<char(t + 'a'); //整型转字符
        preorder(l[t]); 
        preorder(r[t]);
    }
}

int main()
{
    cin>>n;
    for(int i = 0; i < n; ++i) {
        cin>>s;
        if(!i) //根节点
            root = s[0] - 'a'; //字符转整型
        l[s[0] - 'a'] = s[1] - 'a'; //存储左儿子
        r[s[0] - 'a'] = s[2] - 'a'; //存储右儿子
    }

    preorder(root); //先序遍历并输出

    return 0;
}

🦎Tree Recovery

Tree Recovery - UVA 536 - Virtual Judge (vjudge.net)

为了更好理解postorder()函数的过程，想想递归树，也可以对照样例来模拟

比如👇

DBACEGF ABCDEFG
ACBFGED

解释

int len = inorder.find(preorder[l1]) - l2; //左子树长度

👆inorder.find(preorder[l1]) 表示中序中根节点下标，l2表示中序中子树的起始位置

根节点 - 起始 = 左子树长度

AC 代码

#include<iostream>
using namespace std;

string preorder, inorder;

//l1先序起始位置, l2中序起始, n节点数
void postorder(int l1, int l2, int n)
{
    if(n <= 0) return; //递归出口
    int len = inorder.find(preorder[l1]) - l2; //左子树长度
    //先序DBACEGF 中序ABCDEFG  对照样例写递归
    postorder(l1 + 1, l2, len); //递归左子树
    postorder(l1 + len + 1, l2 + len + 1, n - len - 1); //递归右子树
    cout<<preorder[l1]; //输出根节点位置
}

int main()
{
    while(cin>>preorder>>inorder) {
        int len = preorder.size();
        postorder(0, 0, len);
        cout<<endl;
    }

    return 0;
}

🦎Tree

Tree - UVA 548 - Virtual Judge (vjudge.net)

思路

输入二叉树中序，后续序列，求从根到叶子编号之和最小的叶子节点，sum一样就取编号最小的叶子节点。

先根据后序确定根，然后在中序中划分左右子树，还原二叉树，最后先序遍历，并查找根到叶子编号之和最小的叶子节点的编号（权值）。

解释

（1）

stringstream s(line);

将字符串传递给 stringstream 构造函数，后续的int x; while(s>>x); 因为x是int，所以会读取字符串中的int，而不读取空格

（2）

if(!getline(cin, line)) {}

getline 函数会从输入流cin中读取一行数据，并将其存储在字符串变量line中，包含空格和其他特殊字符

（3）

lch[root]=createtree(l1,l2,len);
rch[root]=createtree(l1+len+1,l2+len,m-len-1);

与

findmin(rch[v],sum);

这里解释下lch[] 和 rch[]，两个数组保存的是左，右子树的信息，下标索引为节点编号，也即节点的值，比如 lch[13] = 5; 表示节点13的左儿子为5

（4）

sum_min = 0x7fffffff;

0x 十六进制，0 八进制，0b 二进制

0x7fffffff 就表示 0111 1111 1111 1111 1111 1111 1111 1111，即10进制中 2^31 - 1

十六进制的 7 表示成二进制 0111，十六进制的 f，即 15，表示成二进制 1111

AC 代码

#include<iostream>
#include<sstream> // stringstream
using namespace std;

const int maxn = 10000+5;
int lch[maxn], rch[maxn], in[maxn], post[maxn], n, ans; // in中序, post后序
int sum_min; // 最大int

// 读入带空格字符串
bool read(int *a)
{
    string line;
    if(!getline(cin, line))
        return false; // 读入失败
    stringstream s(line);
    n = 0;
    int num;
    while (s >> num) // num为int，所以只会读取整数
        a[n++] = num; // 得到初始节点总数 n
    return n > 0;
}

// 递归建树
int create_tree(int L1, int L2, int len) // L1中序起始, L2后序起始
{ // len当前子树长度
    if (len <= 0)
        return 0; //空树
    int root = post[L2 + len - 1]; // 当前子树后序最后一个为根, 所以要加上L2
    // 中序中找根节点
    int p = 0;
    while (in[L1 + p] != root)
        p++; // 根节点在中序位置
    lch[root] = create_tree(L1, L2, p); // 递归左子树
    rch[root] = create_tree(L1 + p + 1, L2 + p, len - p - 1); // 递归右子树
    return root;
}

void findmin(int v, int sum) // v当前节点编号值value
{
    sum += v;
    if (!lch[v] && !rch[v]) // 没有左右子树, 即叶子节点
        if (sum < sum_min || (sum == sum_min && v < ans)) {
            ans = v;
            sum_min = sum;
        }
    if (lch[v]) // v 有左子树
        findmin(lch[v], sum); // 递归左子树
    if (rch[v]) // v 有右子树
        findmin(rch[v], sum); // 递归右子树
}

int main()
{
    while(read(in)) {
        read(post);
        create_tree(0, 0, n);

        sum_min = 0x7fffffff; // 记得在此处更新

        findmin(post[n - 1], 0);
        cout<<ans<<endl;
    }
    return 0;
}

🌼5.4 -- 哈夫曼树

1，前置知识

（1）根据维基百科

霍夫曼编码使用变长编码表对源符号（如文件中的一个字母）进行编码，其中变长编码表是通过一种评估来源符号出现机率的方法得到的，出现机率高的字母使用较短的编码，反之出现机率低的则使用较长的编码，这便使编码之后的字符串的平均长度、期望值降低，从而达到无损压缩数据的目的。

（2）

哈夫曼编码（Huffman Coding）多图详细解析_von Libniz的博客-CSDN博客

👍 ---- 知识点介绍，引用别人的就好，省的敲

（3）

为了追求最优编码方案，如果每个字符使用频率一样，我们可以采用固定长度编码

但使用频率不一样的话，需要采用不等长编码，哈夫曼编码就是其中的一个代表

哈夫曼编码广泛用于数据压缩，尤其是远距离通信和大容量数据存储，常用的JPEG图片，就是采用哈夫曼编码压缩的。

基本思想

以字符的使用频率作为权值构建一颗哈夫曼树。

要编码的字符作为叶子节点，出现的频率作为权值。

以自底向上的方式，进行 n - 1 次“合并”。

权值越大的叶子节点，离根越近。

（4）

贪心策略

每次从森林中，找到2棵权值最小的孤儿树，作为左右子树，构造一棵新树，新树权值为2颗孤儿树的权值和，将新树放回森林。

2，实现

（1）数据结构

节点结构体 HnodeType -- 二叉树

typedef struct {
    double weight; // 权值
    int parent, lchild, rchild; // 双亲,左孩,右孩
    char value; // 字符
} HNodeType;

编码结构体 HcodeType -- 与字符一一对应的二进制

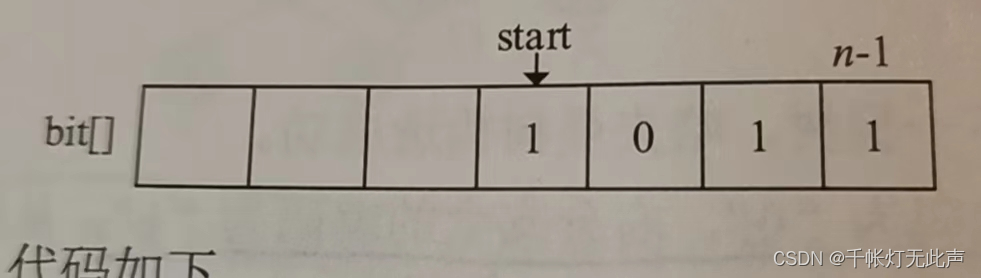
bit[] 存放节点的编码，start 记录开始的下标

逆向编码存储时（从叶子到根），start 从 n - 1 开始依次递减，从后向前存储

读取时，从 start + 1开始到 n - 1，前向后输出，即该字符的编码

为什么存储 -- 后向前；而读取 -- 前向后呢？

这符合哈夫曼树的构造和编码流程，每个字符对应的二进制，都是从根节点开始读的（前向后），但是记录 bit[] 时，是从每一个叶节点出发的（后向前）（详情看前置只是的博客）

typedef struct {
    int bit[MAXBIT]; // 存储编码的数组
    int start; // 编码开始的下标
} HCodeType;

（2）初始化

节点权值为 0

parent, lchild, rchild 为 -1

value 对应字符

然后读入叶子节点权值

（3）循环构造哈夫曼树

集合T中取出双亲为-1且权值最小的两棵树ti, tj，合并为一颗新树zk

int x1, x2; //  最小权值节点的序号
double m1, m2; // 最小权值节点的权值
for (int i = 0; i < n - 1; i++) {
    m1 = m2 = MAXVALUE; // 初始化为最大值, m编号, x序号
    x1 = x2 = -1; // 初始化为 -1
    // 找出所有节点中权值最小, 无双亲节点的两个节点
    for (int j = 0; j < n + i; j++) {
        if (HuffNode[j].weight < m1 && HuffNode[j].parent == -1) {
            // 交换当前最小权值的两棵树
            m2 = m1, x2 = x1; // m1最小, m2次小

            m1 = HuffNode[j].weight; // 最小节点权值
            x1 = j; // 记录序号
        }
        else if (HuffNode[j].weight < m2 && HuffNode[j].parent == -1) {
            m2 = HuffNode[j].weight; // 次小节点权值
            x2 = j; // 记录序号
        }
    }
    /* 更新新树信息 */
    // 设置 parent
    HuffNode[x1].parent = n + i;
    HuffNode[x2].parent = n + i;
    // 设置 child 和 weight
    HuffNode[n + i].weight = m1 + m2;
    HuffNode[n + i].lchild = x1; 
    HuffNode[n + i].rchild = x2;
}

解释

（1）外层 for 循环 n - 1 次

构建哈夫曼树时，假设 n 个叶节点，那么总节点数 2n - 1 个，此时内部节点数 = 总数 - 叶子数 = n - 1

所以循环次数为 n - 1（内部节点数）

（2）初始化权值MAX 和序号 -1

为了保证后续选择序号和权值时，有合适的初始值

（3）内层 for 循环

在当前节点集合中找出权值最小的两个节点x1和x2，并且这两个节点没有双亲节点

（parent == -1）

通过遍历节点集合，比较节点的权值找出最小和次小的节点并记录它们的序号

（4）更新信息

为什么双亲的序号是 n + i 呢

n 表示原始叶子节点的个数，i 表示当前正在处理的第 i 个非叶子节点

保证新节点的编号是唯一的，不会与其他已存在的节点重复

（4）输出哈夫曼编码

回顾

节点结构体 HNodeType

typedef struct {
    double weight; // 权值
    int parent, lchild, rchild; // 双亲,左孩,右孩
    char value; // 字符
} HNodeType;

编码结构体 HCodeType

typedef struct {
    int bit[MAXBIT]; // 存储编码的数组
    int start; // 编码开始的下标
} HCodeType;

代码

解释看注释（详细过程的图解 + 图表 + 代码，请自行看书）

// (用于生成叶子节点编码) 参数1编码结果的HCodeType数组, 参数2叶子个数
void HuffmanCode(HCodeType HuffCode[MAXLEAF], int n) 
{
    HCodeType cd; // 编码信息
    int c, p; // 叶节点和父节点
    for (int i = 0; i < n; i++) { // 遍历所有叶节点
        // 索引0开始, 所以最后一个位置是 n - 1
        cd.start = n - 1; // 临时编码起始位置 n - 1, 后往前
        c = i; // i 为叶子节点编号
        p = HuffNode[c].parent; // 叶节点父亲的编号
        // p != -1保证向上遍历, 直到根节点, 因为根节点没有父亲, p == -1
        while (p != -1) { // 父节点不为 -1
            if (HuffNode[p].lchild == c) 
                cd.bit[cd.start] = 0; // 左 0
            else 
                cd.bit[cd.start] = 1; // 右 1
            cd.start--; // 向前记录编码的 0 / 1
            c = p; // 子变父
            p = HuffNode[c].parent; // 此时的c就是原来的p, 父变爷爷
        } 
        // while循环结束后, 当前叶节点 i 的二进制记录完毕
        // 每个while循环, 都是一条完整的从叶节点到根节点的路径

        /* 叶节点的编码从临时编码cd中复制出来, 放入编码结构体数组 */
        // bit是结构体成员, cd是临时编码结构体, 第 i 个叶节点, 第 j 个编码位置
        // 编码起始位置开始, 依次复制
        // cd.start + 1, 开始, 因为最后多前移了一格, 而这一格没有父节点, bit[]没有记录
        for (int j = cd.start + 1; j < n; j++) // 前往后
            HuffCode[i].bit[j] = cd.bit[j]; 
        HuffCode[i].start = cd.start; // 更新HuffCode中起始位置, 打印时和cd位置一样
    }
}

3，分析

在构造循环哈夫曼树 JuffmanTree() 函数中，

if (HuffNode[j].weight < m1 && HuffNode[j].parent == -1) 为基本语句

外层 i 与内层 j 双层循环

i = 0，该语句执行 n 次

i = 1，n + 1次

...

i = n - 2，执行 n + (n - 2) 次

加起来 (3n - 2) * (n - 1) / 2

而在函数 HuffmanCode() 中，编码和输出的时间复杂度都接近 n^2

所以时间复杂度 O(n^2)

空间复杂度：所需存储空间为节点结构体数组和编码结构体数组

哈夫曼树数组 HuffNode[] 中节点为 n 个，每个节点包含 bit[MAXBIT] 和 start 两个域，

则算法空间复杂度为 O(n * MAXBIT)

4，优化

（1）时间

HuffmanTree() 构造哈夫曼树中，找两个权值最小节点时，使用优先队列，时间复杂度 O(logn)，执行 n - 1 次，总时间复杂度 O(nlogn)

（2）空间

HuffmanCode() 输出哈夫曼编码中，哈夫曼编码数组 HuffCode[] 中，定义一个动态分配空间的线性表来存储编码（每个线性表的长度都为实际编码长度，大大节省空间）

⚽刷题

🦎围栏修复

Fence Repair - POJ 3253 - Virtual Judge (vjudge.net)

3253 -- Fence Repair (poj.org)

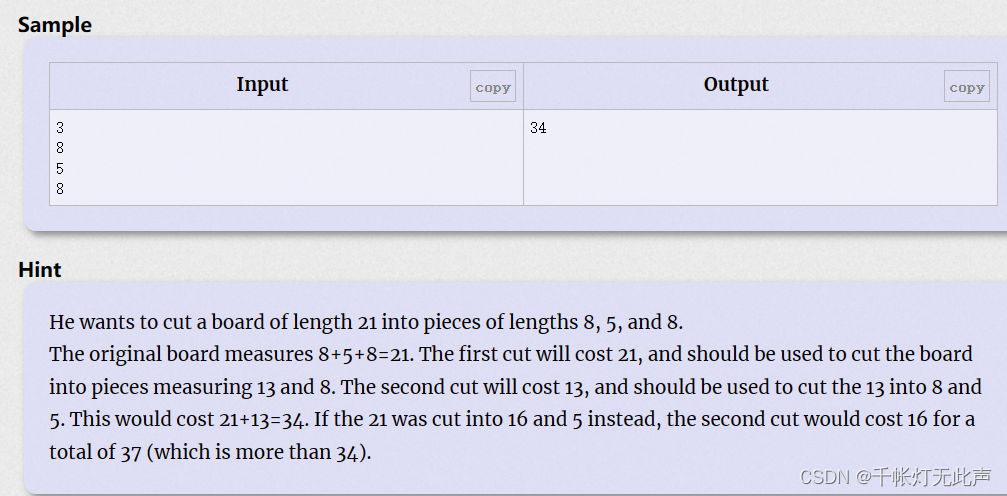
样例解释

思路

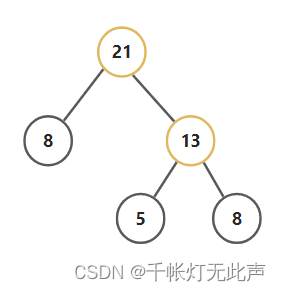
21 + 13 = 34

容易发现，要取最小值，正向思考，每次去掉当前最大值，逆向则符合哈夫曼树的构造

（每次取两个最小的合并，直到合并为一棵树，每次合并的结果就是切割的费用）

（优先队列默认最大堆，队头（堆顶）元素始终是最大值，这里我们需要设置最小堆）

使用优先队列（最小值优先），每次都弹出两个最小值 t1, t2， t = t1 + t2， sum += t，将 t 入队，继续，直到队空。sum为所需花费

假设20000个木板，每块50000米，哈夫曼构造，结果 sum = 10^4 * (5*2 + 5*3 + ... + 5*20000) = 5 * 10^4 * (2 + 3 + ... + 20000) ≈ 5 * 10^4 * 2 * 10^8 = 10^13（用long long）

priority_queue三个参数👇

std::priority_queue - cppreference.com

关于第 2 参数

用于存储元素的底层容器类型。容器必须满足 SequenceContainer 的要求，其迭代器必须满足 LegacyRandomAccessIterator 的要求

priority_queue常用函数

AC 代码

注意测试样例

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;

int main()
{
    long long sum = 0;
    int n, t, t1, t2;
    priority_queue<int, vector<int>, greater<int> > q;

    scanf("%d", &n);
    for (int i = 0; i < n; ++i) {
        scanf("%d", &t);
        q.push(t);
    }

    if (q.size() == 1) {
        sum += q.top();
        q.pop();
    }

    while (q.size() > 1) {
        t1 = q.top(), q.pop();
        t2 = q.top(), q.pop();
        t = t1 + t2, q.push(t);
        sum += t;
        // cout << sum << endl;
    }

    printf("%lld", sum);
    return 0;
}

🦎信息熵

Entropy - POJ 1521 - Virtual Judge (vjudge.net)

Huffman模板题

The text strings will consist only of uppercase alphanumeric characters and underscores (which are used in place of spaces)

文本字符串只包含大写字母数字字符和下划线（用来代替空格）

样例解释

对于输入中的每个文本字符串，输出 8 位 ASCII 编码的比特长度、最佳无前缀变长编码的比特长度，以及精确到小数点后一位的压缩比

思路

最佳无前缀可变长度编码（optimal prefix-free variable-length encoding）

就是哈夫曼编码

首先根据字符串统计每个字符出现频率，然后按频率构造哈夫曼树，计算总的编码长度

（多次读入）

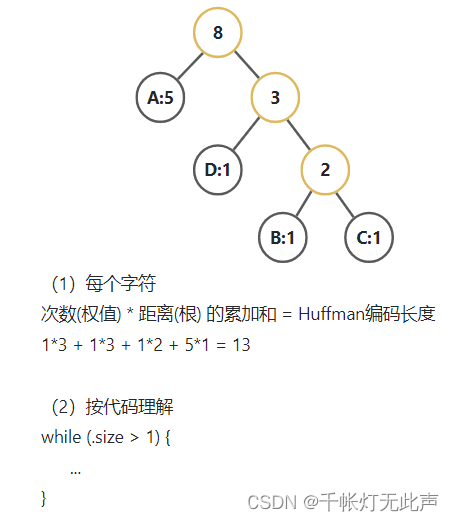
理解

这里可以按2种方式理解

AC 代码

源码是漏了考虑数字，但是，有点还是不错，它有对一个字符的特判，初始化 ans = s.size()，这是我不足的地方

有个坑，double 的 printf 输出用 .f ，而 scanf 输入用 .lf

第二个坑，需要特判一个字符的情况，比如 aaaa，输出应该是 32 4 8.0

所以 if (q.size() == 1) ans = s.size()

#include<iostream>
#include<cstring> //memset()
#include<cstdio> // printf()
#include<queue>
using namespace std;

int a[200]; // 字符出现次数

int main()
{
    string s;
    int ans, t1, t2, t, n;
    while (1) {
        cin >> s;
        if (s == "END") break;

        memset(a, 0, sizeof(a)); // 初始化
        ans = 0, n = s.size();

        for (int i = 0; i < n; ++i) {
            if (s[i] == '_')
                a[99]++; // _代替空格
            else
                a[s[i] - '0']++; // 字符出现次数
        }

        // 最小值在堆顶的优先队列
        priority_queue<int , vector<int>, greater<int> > q;

        for (int i = 0; i <= 99; ++i)
            if (a[i]) q.push(a[i]);

        // 特判: 只出现一种字符
        if (q.size() == 1) ans = n; // 注意这里是n, 每个字符用一个0/1表示, n个0/1

        while (q.size() > 1) {
            t1 = q.top(), q.pop();
            t2 = q.top(), q.pop();
            t = t1 + t2;
            ans += t, q.push(t);
        }

        printf("%d %d %.1f\n", 8*n, ans, (double)8*n / ans);
    }

    return 0;
}

也可以不用 a[] 来统计数字 + 大写字母 + 下划线，出现次数

直接对字符串 s 排序，然后顺序判断每个字符出现次数

🦎转换哈夫曼编码

Inverting Huffman - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

Inverting Huffman - UVA 12676 - Virtual Judge (vjudge.net)

思路

本题不是常规（简单）的哈夫曼编码问题，不是给出字符出现次数，来求最短编码长度；

而是给定编码长度，即离根节点的距离

编码长度 = 离根节点距离（与出现次数成反比）

给定编码长度，已知长度越大，离根节点越远，权值越小（出现次数越小）

那么我们假定编码长度最大的为1，然后秉持着 “每一层当前节点权值，至少是下一节点权值的最大值”，即可找到最短编码长度

如果当前节点权值比下一层最大值小，那么应该出现在下一层，而不会出现在本层

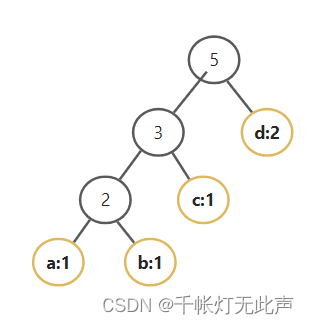
举个例子

4 // 4个不同字符
3 1 2 3 // 每个字符编码长度

3 1 2 3 即 3 3 2 1，那么可以假定离根节点距离最大，为 3 的两个字符，权值都为 1👇

那么最短编码长度为 5

算法设计

根节点权值最大可能：1 2 3 5 8 13 21 34 55 89 144 ... 到第50个数，第49层，用 long long

读取输入的字符个数 n

清空之前的数据，对深度数组 deep[] 进行清空操作，确保每次循环都是从空数组开始

初始化变量 maxd 为 0（最大深度）

读取每个字符对应的深度 x

a. 更新 maxd，如果当前深度 x 大于 maxd，则更新 maxd 的值为 x

b. deep[x] ，第 x 层中，初始化每个节点权值为 0

向上遍历处理树的每一层，从最大深度开始，直到第 0 层

a. 当前层

i. 节点的值为 0，找到一个字符，根据贪心，赋值为上一层最大元素

ii. 对当前层的节点进行排序

b. 合并节点，并放入上一层

i. t = t1 + t2，t 加入上一层

c. 更新 temp 当前层最大值

输出第 0 层第 1 个元素的值，即 *(deep[0].begin())

AC 代码

#include<iostream>
#include<algorithm> // sort()
#include<cmath> // max()
#include<vector>
using namespace std;

const int maxn = 55; // 最大深度
vector<long long> deep[maxn]; // 每个元素都是vector数组

int main()
{
    int n, x; // 第 x 层, n 个字符

    while (cin >> n) {

        // 清空
        for (int i = 0; i < n; ++i)
            deep[i].clear(); // 清空vector数组

        // 初始化
        int maxd = 0; // 最大深度
        for (int i = 0; i < n; ++i) {
            cin >> x; // 第 x 层, 即到根节点距离 x
            maxd = max(maxd, x);
            deep[x].push_back(0); // 第 x 层每个节点初始化为0
        }

        // 向上遍历
        long long temp = 1; // 该层排序后最大元素 (最后一个)
        for (int i = maxd; i > 0; --i) { // 最大深度开始

            for (int j = 0; j < deep[i].size(); ++j)
                if (!deep[i][j])
                    deep[i][j] = temp; // 第 i 层没有权值的节点, 被上一层最大值赋值
            sort(deep[i].begin(), deep[i].end()); // 第 i 层排序

            // 合并后放入上一层
            for (int j = 0; j < deep[i].size(); j += 2)
                deep[i - 1].push_back(deep[i][j] + deep[i][j + 1]);

            // 更新 temp 为第 i 层最大值
            temp = *(deep[i].end() - 1); // 最大值即最后一个元素
        }
        cout << *(deep[0].begin()) << endl; // 输出第 0 层第 1 个元素
    }

    return 0;
}