100. 相同的树 

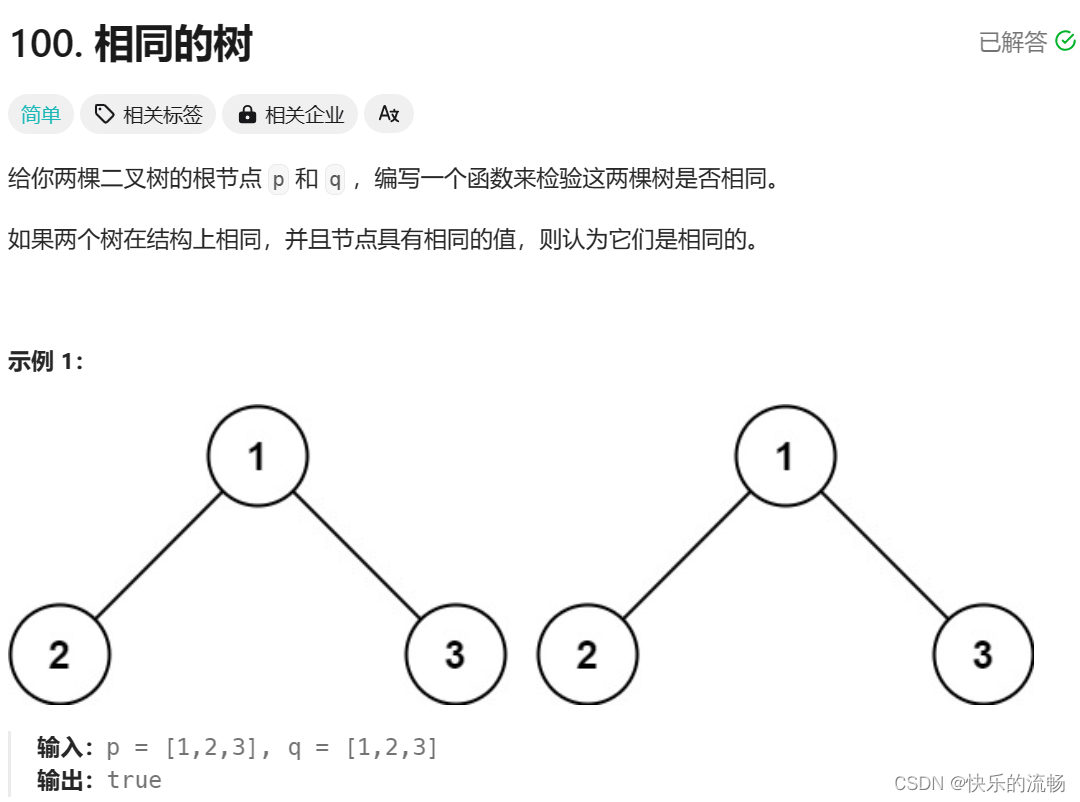
关于树的递归问题，永远考虑两方面：返回条件和子问题

1. 先考虑返回条件，如果当前的根节点不相同，那就返回false（注意，不要判断相等时返回什么，因为当前相等并不能说明后面节点相等，所以要转换为不相等返回什么）
2. 但是还要考虑为空的情况，如果两个树的根节点都为空，则返回true（只有经过层层比较，当比较到最后都为空树时，才返回true）；如果一个为空一个不为空，则返回false
3. 最后考虑子问题，当前树的根节点比较完毕，那就转化为左子树和右子树进行递归比较 

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
    if (p == NULL && q == NULL)
    {
        return true;
    }

    if (p == NULL || q == NULL)
    {
        return false;
    }

    if (p->val != q->val)
    {
        return false;
    }

    return isSameTree(p->left, q->left)
        && isSameTree(p->right, q->right);
}

965. 单值二叉树 

思路：判断单值的条件，就是让父节点的值与两个孩子的值相等 

具体方法：

• 如果为空树，则返回true（必然走到末尾，那前面的值判断都通过）
• 当前节点与左孩子的值进行比较，如果不相等，则返回false（注意，加上条件判断，保证左孩子不为空，防止对空指针的解引用）
• 同理，当前节点与右孩子的值进行比较，如果不相等，则返回false
• 最后的子问题，则返回左子树与右子树的返回值的逻辑与，只要不满足上述条件，就一直往下递归

bool isUnivalTree(struct TreeNode* root)
{
    if (root == NULL)
    {
        return true;
    }

    if (root->left && root->val != root->left->val)
    {
        return false;
    }

    if (root->right && root->val != root->right->val)
    {
        return false;
    }

    return isUnivalTree(root->left)
       && isUnivalTree(root->right);
}

101. 对称二叉树

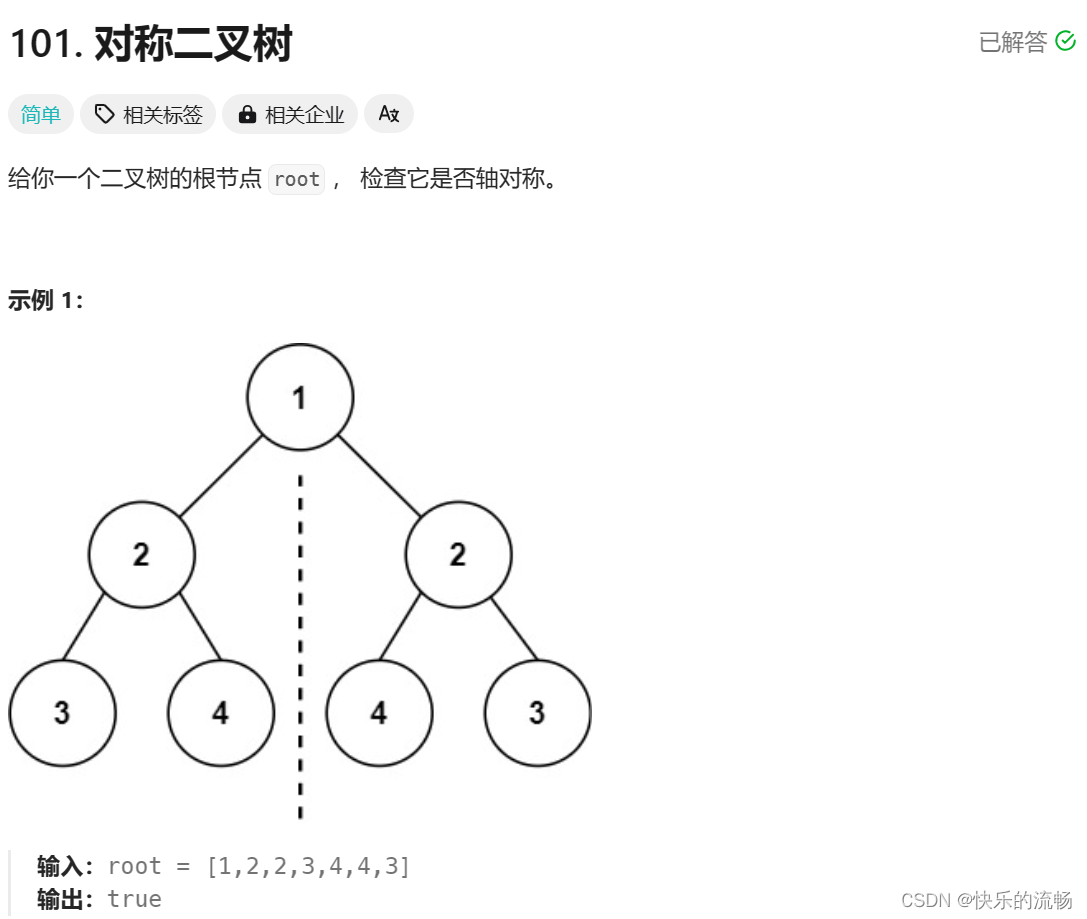
 思路：因为要用左子树的左支（右支）和右子树的右支（左支）进行比较，所以再创建一个子函数接受两个参数。

具体方法：

1. 如果左右子树根节点都为NULL，则返回true
2. 如果左右子树根节点一个为空一个不为空，则返回false
3. 如果左右子树根节点非空，并且不相等，则返回false
4. 子问题划分为，左子树的左支与右子树的右支相比，左子树的右支与右子树的左支相比，检查是否对称，如果都对称，则返回true

bool _isSymmetric(struct TreeNode* left, struct TreeNode* right)
{
    if (left == NULL && right == NULL)
    {
        return true;
    }

    if (left == NULL || right == NULL)
    {
        return false;
    }

    if (left->val != right->val)
    {
        return false;
    }

    return _isSymmetric(left->left, right->right)
        && _isSymmetric(left->right, right->left);
}

bool isSymmetric(struct TreeNode* root)
{
    return _isSymmetric(root->left, root->right);
}

144. 二叉树的前序遍历 

 首先，这题要注意的是，它要求动态开辟一个数组，将二叉树的值以前序遍历的顺序放入，最后再返回该数组，所以它跟我们之前直接前序遍历还是不一样的，变得更加复杂了。

具体实现思路：

1. 这道题，因为数组大小不确定，所以题目传进来一个返回型参数（returnSize），那么我们则把求二叉树的节点个数的函数写出来（对现在的我们来说，应该挺简单的），再将节点个数求出，赋给returnSize
2. 动态开辟数组，大小为二叉树节点个数个整型空间
3. 创建前序遍历子函数，用来真正实现以前序遍历的顺序，将二叉树的值放入数组
4. 注意，这里如果传进来i，那么会因为其为局部变量，递归时内层函数栈帧i++，并不会影响到外层函数栈帧中的i，导致数组中有些值被重叠覆盖，而有些值未初始化（随机值）。所以，正确的做法，是传入i的地址，对其解引用++

 传入i时，会造成内存错误，如下图：

 

void _preorderTraversal(struct TreeNode* root, int* a, int* pi)
{
    if (root == NULL)
    {
        return;
    }

    a[(*pi)++] = root->val;
    _preorderTraversal(root->left, a, pi);
    _preorderTraversal(root->right, a, pi);
}

int BTreeSize(struct TreeNode* root)
{
    return root == NULL ? 0 : BTreeSize(root->left) + BTreeSize(root->right) + 1;
}

int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
    *returnSize = BTreeSize(root);
    int* a = (int*)malloc(*returnSize * sizeof(int));

    int i = 0;
    _preorderTraversal(root, a, &i);

    return a;
}