微❤关注“电气仔推送”获得资料(专享优惠)
本模型主要是基于一致性理论的自适应虚拟阻抗、二次电压补偿以及二次频率补偿,实现功率均分,保证电压以及频率稳定性。
一致性算法
分布式一致性控制主要分为两类:协调同步和跟踪同步。所谓协调同步是指将系统各个节点的某个控制目标同步到一个未规定或不可控的相同值,也称无领导者的一致性控制。跟踪同步控制是有领导者的一致性控制,其最终目的是将系统的其他各个节点的某个控制目标追踪到领导者状态,即向领导者看齐。对于本节要介绍的无功分配一致性控制采用的是无领导者的协调同步一致性控制。
分布式协同控制是通过建立稀疏通信网络的有向图实现的。将信息状态xi分配到通信节点i 上,每个节点都需要获取自身信息以及有向图上相邻节点的信息以更新其状态xi,基于连续一致性算法根据不同一致性控制采用不同更新规则。
针对协调同步问题,采用无领导者的一致性算法:
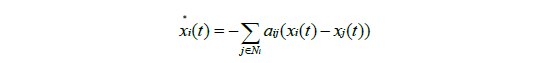
针对跟踪同步问题,采用有领导者的一致性算法:
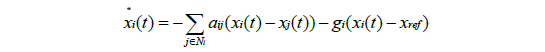
在分析功率分配问题时,需要把系统中所有节点的状态量niQi同步到一个未规定的共同值,因此,这里采用无领导者的一致性算法。
基于一致性算法的自适应虚拟阻抗控制
为了实现无功功率按比例分配,需要把系统中所有节点的状态量niQi同步到一个未规定的共同值,是一阶线性多智能体系统的协调同步问题。
![]()
其中, UQi是一个辅助控制,根据一致性控制协议,辅助控制是根据每一台DG 的自身信息和有向图中与其相邻的DG 信息得到的,即每一台DG 的无功功率控制器将本地无功分配信息与相邻的无功分配信息进行比较得到无功不匹配。
![]()
其中,cQ 是控制增益,eQi 为同步误差,即i 节点与相邻节点的无功分配误差
![]()
aij是邻接矩阵AG的元素, AG反映了通信网络的状态,如果通信网络发生变化,则AG 也会随之变化。
无功功率分配误差通过辅助控制uQ反馈到一个比例积分(PI)控制器,得到虚拟阻抗矫正项。虚拟阻抗矫正项动态更新虚拟阻抗的值。
![]()
如果各DG 的输出无功不能按各自的额定无功成比例分配,则通过分布式通信网络获取相邻DG 的无功分配信息,以更新本地的无功分配误差按照下式自适应地调节自身的虚拟电感。
![]()
同时采用自适应虚拟电阻可对微电网系统提供一定的阻尼效果
![]()
需要注意的是,这种方法不是直接调节每个DG 的无功功率,而是将每个DG 的虚拟阻抗调整到一个值,并且使得各DG 的等效阻抗与无功功率成反比,以消除由于线路阻抗不匹配所造成的无功功率分配误差。

基于一致性算法的二次电压补偿
电压恢复二次控制是将各DG 的参考电压幅值Vfi 同步到参考值 Vfref ,属于跟踪同步问题,故uvi 是根据有领导者的跟踪同步一致性算法确定的:

而Vfref 是根据公共母线电压Vpcc 和其参考电压Vref pcc 通过一个 PI 控制器确定的。
![]()
基于一致性算法的二次频率补偿
二次频率补偿类似于二次电压补偿
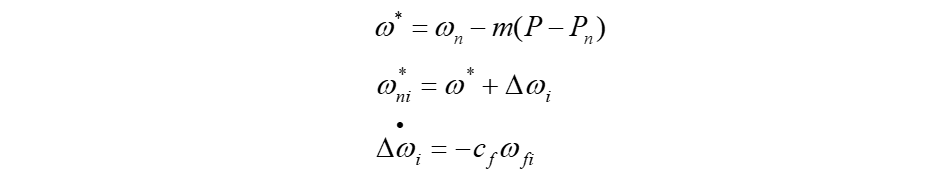
cf是控制增益,wfi用来实现频率控制的跟踪误差。

由公共母线参考频率wPCC和参考电压wPCCref通过PI控制后得到wfref。

仿真主体模型:
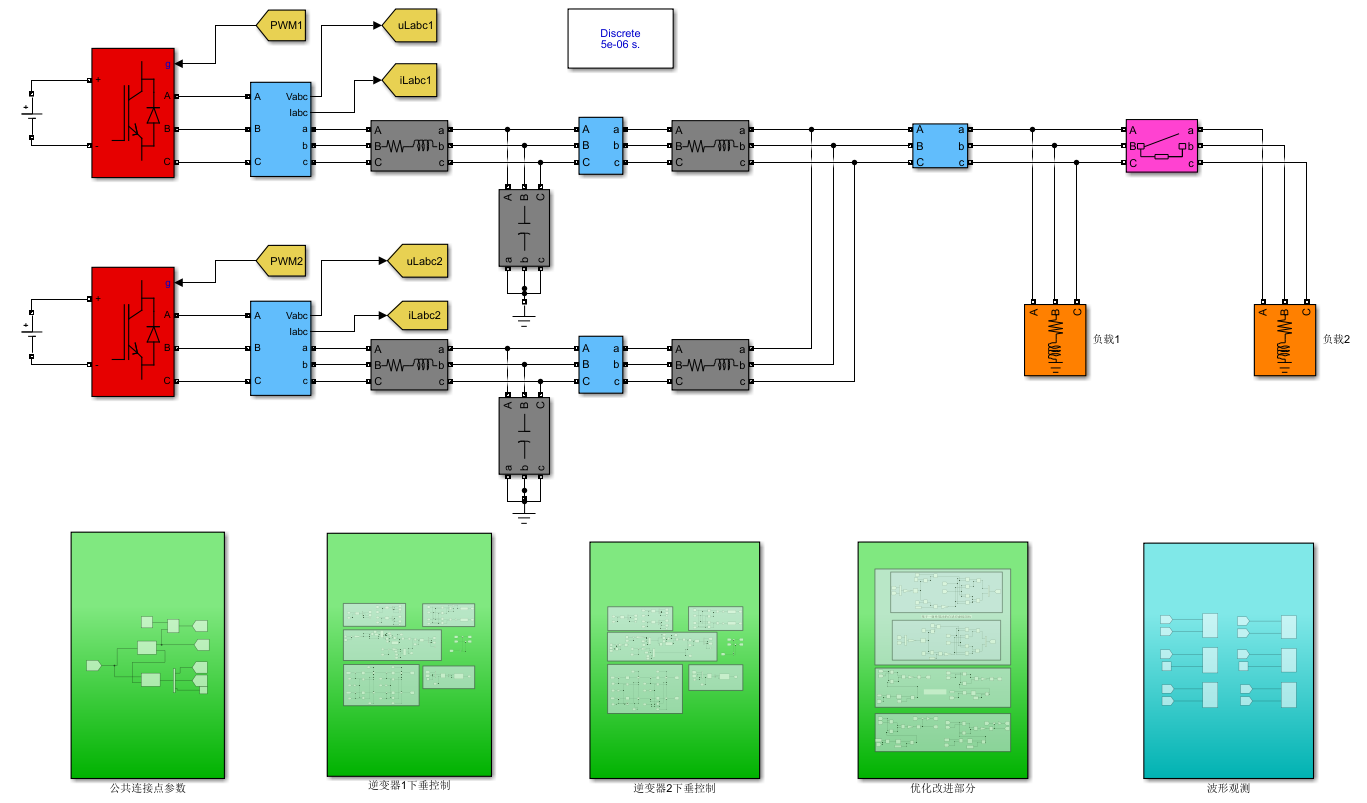
优化控制部分:

功率输出波形:
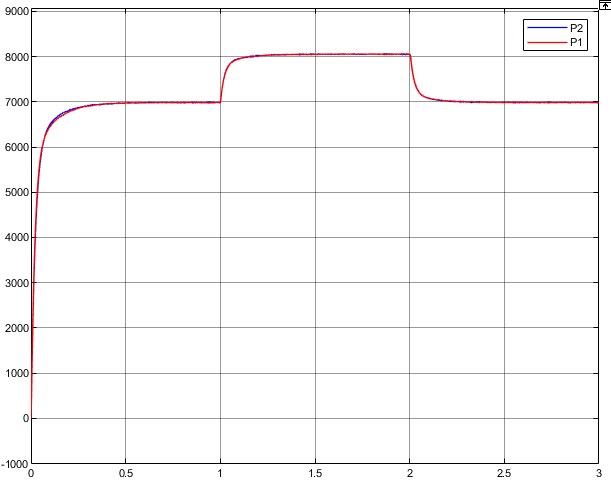

因为自适应虚拟阻抗的加入,有功、无功都能达到均分效果。
电压补偿:


上图为没有加入二次电压补偿的公共点电压,下图为加入二次补偿后的效果。因为二次电压补偿后,公共点电压不会因为虚拟阻抗的引入而导致电压跌落,快速回复到稳定值。
频率补偿:

上图为没有加入二次频率补偿的公共点电压,下图为加入二次频率补偿后的效果。因为二次频率补偿后,频率会稳定在50Hz,增加了系统的稳定性。
参考文献:
基于一致性理论的孤岛微电网分布式控制策略研究_熊德超
微电网中分布式电源改进下垂控制研究_曾信毅