首先在讲这个定理前,首先科普一下前置知识
约数:
何为约数,只要能整除n的整数就是n的约数,举个例子,3的约束是1和3因为1和3能整除3
质数:
除了这个数字本身和1以外没有其他因子的数字就叫质数,也就是说只能被1和它本身整除。当然1不算质数。2是最小的质数。
分解质因数的定理
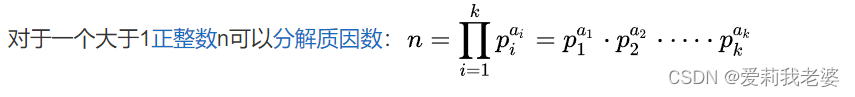
也就是说任意一个大于一的正整数可以分解为从无数质数累乘。
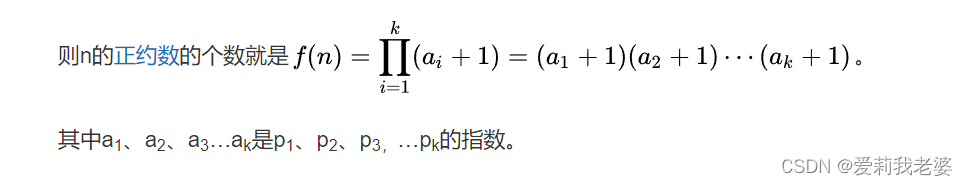
而一个数的正约数就是上面的公式。
来解释一下把:

首先在讲这个定理前,首先科普一下前置知识
何为约数,只要能整除n的整数就是n的约数,举个例子,3的约束是1和3因为1和3能整除3
除了这个数字本身和1以外没有其他因子的数字就叫质数,也就是说只能被1和它本身整除。当然1不算质数。2是最小的质数。
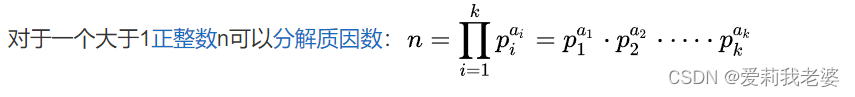
也就是说任意一个大于一的正整数可以分解为从无数质数累乘。
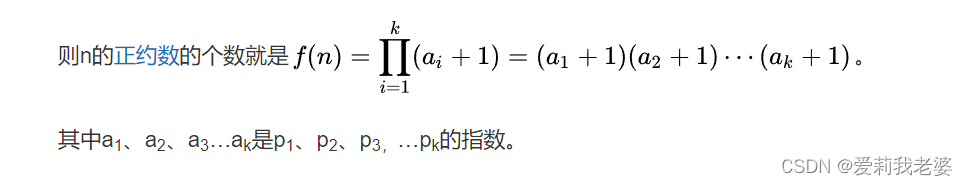
而一个数的正约数就是上面的公式。
来解释一下把:

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1227912.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!