文章目录
- 导论
- 随机过程
- 相关
学习视频来源:https://www.bilibili.com/video/BV18p4y1u7NP?p=1&vd_source=5e8340c2f2373cdec3870278aedd8ca4
将持续更新——
第一次更新:2023-11-19
导论
教材:《随机过程及其应用》陆大絟.张颢
参考:A.Papoulis,S.U.Pillai,帕普里斯.Probability, random variables and stochastic processes[M].机械工业出版社,2013.
Kiyosi Ito.Stochastic Processes
课程理念
No Reading.No Learning.
No Writing.No Reading.
No Writing.No listening.
No Data.No Truth.(获取真实数据,建立在仿真上的数据不可靠)
No Analysis.No Understand.(能用符号向大家说明)
No Programing.No Cognition.(解析的东西可以让我们理解,但是未必能让我们形成直觉,但是认知可以很好的和我们的直觉相结合)
随机过程
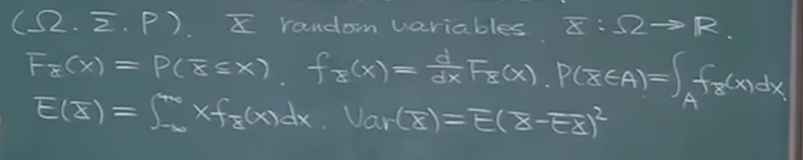
映射是没有随机性的,只是映射到实轴上进行量化
随机过程有一组随机变量,当我们把随机变量的角标等同于空间时,就是随机场。
随机变量常用的关联方式:
- 线性相关
- 马尔可夫性
- 鞅论martingale
相关
相关时一种二元的关系,
X
X
X和
Y
Y
Y隶属于同一个概率空间
P
P
P

- 独立:一个变量的变化对另一个变量的分布情况没有任何影响
- 不独立不相关
- 相关
相关的度量方式
采用均方度量时:
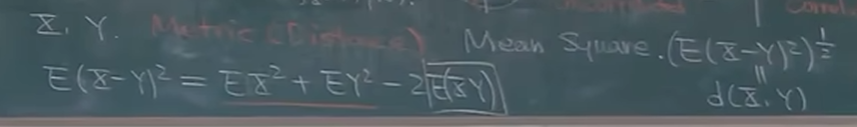
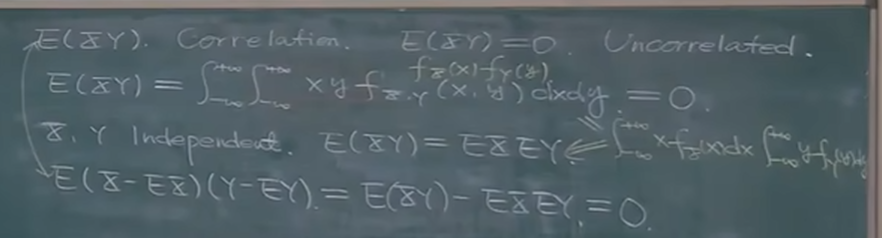
不相关但是不独立的例子
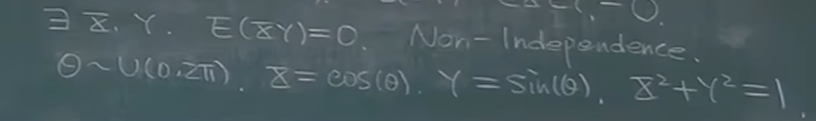

独立是两个随机变量没有联系,相关是两个随机变量有微弱联系
相关系数
通俗理解:两个人之间的关系受个人自身情况的限制
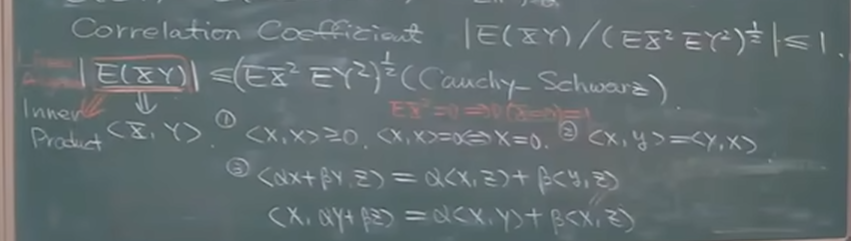
相关是一种内积,满足内积的三个条件。
柯西不等式的证明与举例
E
(
X
Y
)
≤
(
E
X
2
E
Y
2
)
E(XY)\le(EX^2EY^2)
E(XY)≤(EX2EY2)
构造自身的内积
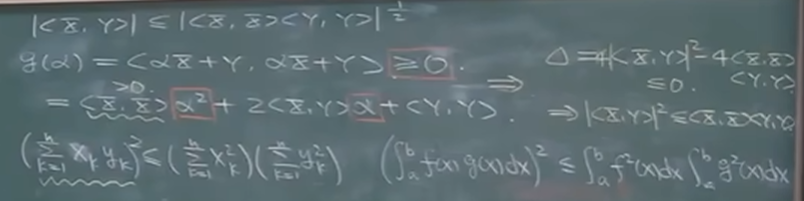
相关的几何看法
内积(相关)能够代表角度
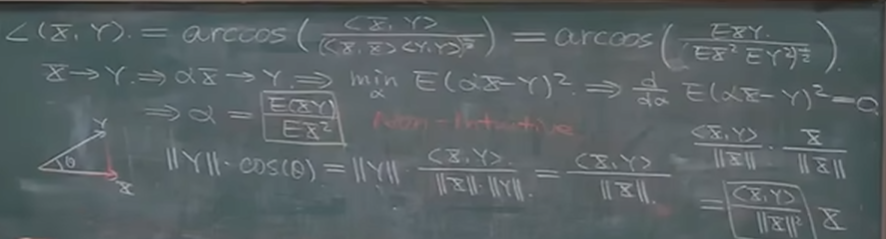
随机过程的相关
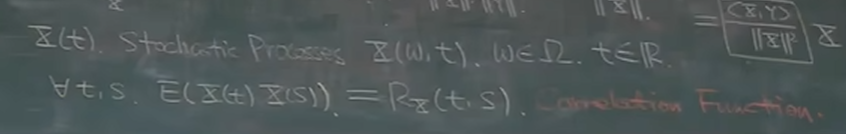
平稳性假设
好假设的要素:陈述简单;进展很快;广泛存在
宽平稳:
R
x
(
t
+
τ
,
s
+
τ
)
=
R
x
(
t
,
s
)
R_x(t+\tau,s+\tau)=R_x(t,s)
Rx(t+τ,s+τ)=Rx(t,s)
R
x
(
t
,
s
)
=
R
x
(
t
−
s
)
=
R
x
(
τ
)
,
τ
=
t
−
s
R_x(t,s)=R_x(t-s)=R_x(\tau),\tau=t-s
Rx(t,s)=Rx(t−s)=Rx(τ),τ=t−s
例:相位调制

例:随机电报信号
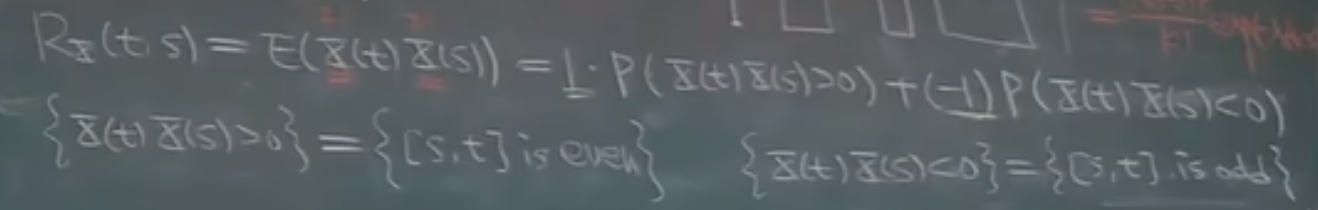
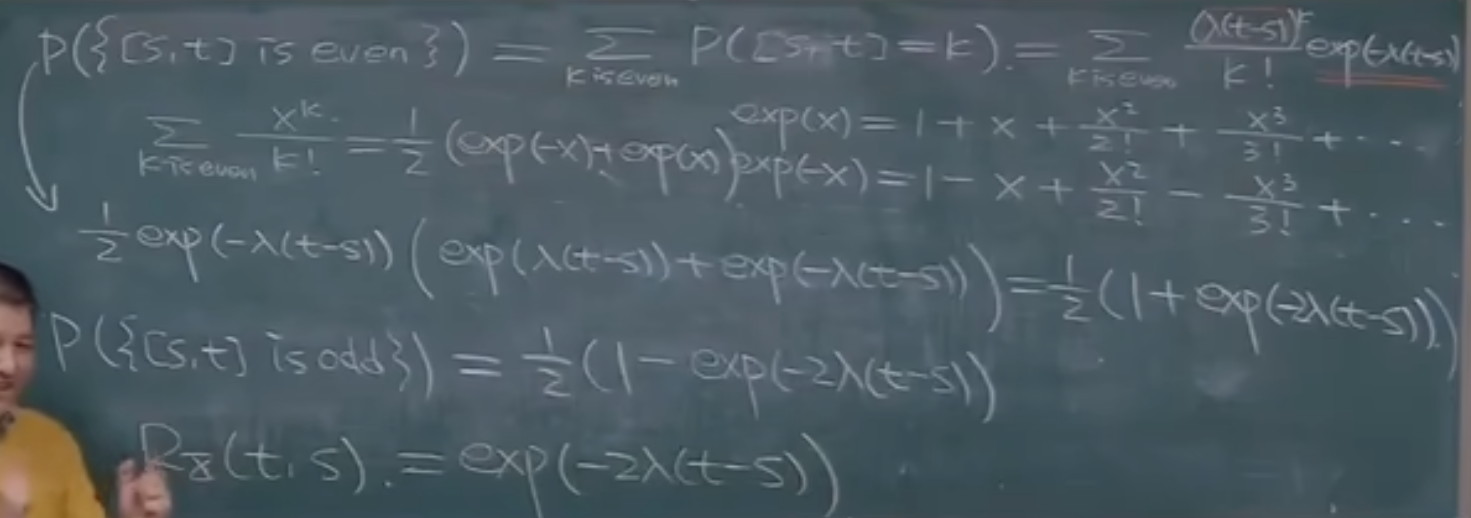





![[AI]ChatGPT4 与 ChatGPT3.5 区别有多大](https://img-blog.csdnimg.cn/fa98ee2c1eef427a88412f9bc6483e55.png)
