【文末送书】今天推荐一些考研数学优质书籍,带你筑牢知识体系
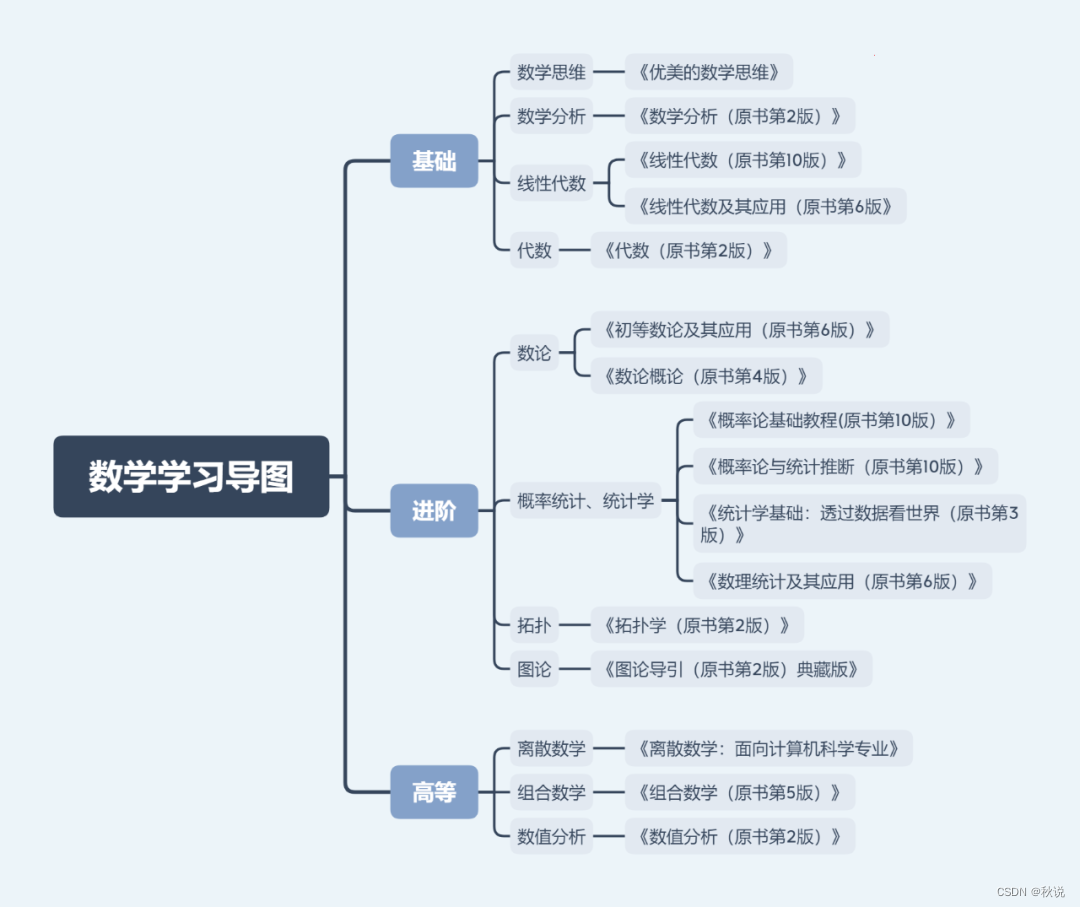
目录
- 导语
- 优美的数学思维:问题求解与证明
- 数学分析
- 线性代数
- 线性代数及其应用
- 代数
- 初等数论及其应用
- 数论概论
- 概率论基础教程
- 概率论与统计推断
- 统计学基础:透过数据看世界
- 数理统计及其应用
- 拓扑学
- 图论导引
- 离散数学:面向计算机科学专业
- 组合数学
- 数值分析
- 文末送书
导语

导读:关于大学数学教材的吐槽似乎从来没停止过。有人慨叹:数学教材晦涩难懂。错!难懂,起码还可以读懂。数学教材你根本读不懂;也有人说:数学教材简直就是天书。
数学教材有好有坏,这话不假,但更多情况下是适合与不适合。不知道怎么选择?这些国内外数百所高校的核心教材,畅销几十年的神作,赶快囤起来慢慢啃吧!

优美的数学思维:问题求解与证明
(原书第2版)
作者:约翰·P.丹吉洛 道格拉斯·B.韦斯特
译者:汪荣贵、孙毅、张桂芸
推荐语:让热爱数学的人体会到绝处逢生的喜悦,让讨厌数学的人从此爱上数学。以大量生动有趣的问题求解实例为背景,使用通俗易懂的语言,深入浅出地介绍优美的数学思维和严谨的证明方法。

数学分析
(原书第2版)
作者:[美] 汤姆·M.阿波斯托尔
译者:邢富冲 邢辰 李松洁 贾婉丽
推荐语:一部现代数学名著。自20世纪70年代面世以来,一直受到西方学术界、教育界的广泛推崇,被许多知名大学指定为教材。
本书是在“高等微积分”的水平上阐述数学分析中的论题,提供了从初等微积分向实变函数论及复变函数论中的高等课程的一种过渡,而且介绍了某些涉及现代分析的抽象理论.内容既涵盖我国大学的数学分析课程的内容,又包括勒贝格积分及柯西定理和留数计算等。

线性代数
推荐语:Leon的线性代数入门经典教材,自1980年初版以来,畅销40多年,已经更新到第10版,中文版累计销售十几万册,配习题+答案。尽量以简单直白的方式讲授线性代数基础知识,第10版更加突出可视化效果,增加了很多图示。

线性代数及其应用
(原书第6版)
作者:戴维·C.雷 史蒂文·R.雷 朱迪·J.麦克唐纳
译者:刘深泉 陈玉珍 张万芹 等
推荐语:线性代数经典教材全新升级,国内外数百所高校核心教材,中文版累计销售20余万册。线性代数应用典范,开创理论与实际应用相结合的先河。

代数
(原书第2版)
作者:[美] 阿廷(Michael Artin)
译者:姚海楼 平艳茹
推荐语:著名代数学家与代数几何学家Michael Artin在代数领域数十年的智慧和经验结晶,配习题。书中既介绍了矩阵运算、群、向量空间、线性变换、对称等较为基本的内容,又介绍了环、模型、域,伽罗瓦理论等较为高深的内容。

初等数论及其应用
(原书第6版)
作者:[美] Kenneth H.Rosen
译者:夏鸿刚
推荐语:Kenneth H. Rosen的数论课程的经典教材,被美国加州大学伯克利分校、伊利诺伊大学、得克萨斯大学等数百所名校采用。三类习题由易到难,理论结合实践。

数论概论
(原书第4版)
作者:[美] 约瑟夫H.西尔弗曼
译者:孙智伟 吴克俭 卢青林 曹惠琴
推荐语:数论经典入门教材新版,面向非数学专业,讲解生动有趣,注重数学思维的培养。

概率论基础教程
(原书第10版)
作者:谢尔登·M.罗斯(Sheldon M. Ross)
译者:梁宝生 童行伟
推荐语:经过锤炼的优秀教材,已在世界范围内畅销三十多年推荐语:经典概率论教材。通过大量的例子系统介绍了概率论的基础知识及其应用。

概率论与统计推断
(原书第10版)
作者:罗伯特·V. 霍格 艾略特·A. 塔尼斯 戴尔·L.齐默曼
译者:王璐 马锋
推荐语:本书是一本优秀的教材,由经验丰富的统计学家撰写,全面介绍概率论和统计推断的核心内容,强化基本数学概念,同时辅以大量现实示例和应用,帮助读者了解这些重要概念之间的关系,从而更好地建立概率模型,做出更好的推断和决策。

统计学基础:透过数据看世界
(原书第3版)
作者:罗伯特·古尔德 丽贝卡·王 科琳
译者:田金方
推荐语:人人可读的统计学图书。通过本书,读者可以学会对数据进行批判性思考,审慎地评价他人的论点。

数理统计及其应用
(原书第6版)
作者:理查德·J.拉森 莫里斯·L.马克斯
译者:王璐 赵威 卢鹏 等
推荐语:本书讲解了概率论与数理统计方面的基础知识及相关应用、还有多种实验设计,阐述严格,证明简练,案例丰富,用大量的真实数据分析案例,帮助读者对数理统计形成较为全面的理解。

拓扑学
(原书第2版)
作者:曼克里斯(Munkres,J.R.)
译者:熊金城 等
推荐语:概念引入自然,循序渐进。对于疑难的推理证明,将其分解为简化的步骤,不给读者留下疑惑。此外,书中还提供了大量练习,可以巩固加深学习的效果。严格的论证、清晰的条理、丰富的实例,让深奥的拓扑学变得轻松易学。

图论导引
(原书第2版)典藏版
作者:道格拉斯·B. 韦斯特
译者:李建中 骆吉洲
推荐语:搭上图计算新风口的最佳船票!证明与应用并举是该书的一个重要特点,书中对所有定理和命题给出了完整的证明,同时讨论了大量的实例和应用,并提供了1200多道习题。

离散数学:面向计算机科学专业
作者:克利福德·斯坦 罗伯特·L.戴斯得尔 肯尼斯·博加特
译者:马帅 秦波 罗杰 伍前红
推荐语:超过50万人阅读的算法经典《算法导论》作者新作!从计算机科学专业需求出发,全面介绍离散数学知识。明确了“为何学”和“有何用”。

组合数学
(原书第5版)
作者:Richard A. Brualdi
译者:冯速 等
推荐语:本书是系统阐述组合数学基础、理论、方法和实例的优秀教材,出版三十多年来多次改版,被MIT、哥伦比亚大学、UIUC、威斯康星大学等众多国外高校采用,对国内外组合数学教学产生了较大影响,也是相关学科的主要参考文献之一。

数值分析
(原书第2版)
作者:Timothy Sauer
译者:裴玉茹 马赓宇
推荐语:本书是系统阐述组合数学基础、理论、方法和实例的优秀教材,出版30多年来多次改版,被MIT、哥伦比亚大学、UIUC、威斯康星大学等众多国外高校采用,对国内外组合数学教学产生了较大影响,也是相关学科的主要参考文献之一。
文末送书
本次活动一共赠书1本,评论区抽取1位粉丝免费送出。
参与方式如下:
点赞收藏文章、评论不少于10字,即可参加。
活动时间:截至2023-11-25 17:00:00
通知方式:通过私信联系中奖粉丝。