proverif-系列文章目录
- 【proverif】proverif的下载安装和初使用
- 【proverif】proverif的语法-解决中间人攻击-代码详解
- 【proverif】proverif的语法2-各种密码原语的编码 (本文)
文章目录
- proverif-系列文章目录
- 前言
- 铺垫知识
- 一、对称加密
- 二、非对称加密
- 三、Diffie-Hellman密钥协议
- 四、HASH function
- 五、数字签名
- 5.1 带消息恢复的签名
- 5.2 带消息恢复的概率签名
- 六、消息验证码(MAC)
- 总结
前言
在官方文档中,给出了部分密码原语(例如:对称加密、非对称加密等)的详细编码例子,接下来我们可以通过学习官方例子代码,从而进行仿写并编写出自己需要的协议编码。
官网页数很多,而纵观全网关于proverif的相关学习资料很少,这看似是一块很难啃的骨头,但是没关系,再多的讲解资料都不如官方的使用手册来的详细。所以现在我们已经拿到寻宝图的真经,跟着本博客猪一起遨游proverif的知识海。
铺垫知识
- 宏机制:包含不止一个构造函数或析构函数应用程序的术语会重复多次。ProVerif提供了一种宏机制,以便定义表示该术语的函数符号并避免重复。
- or fail: 每个参数的类型之后,允许用户在某些参数失败的情况下控制函数宏的行为。果存在or fail并且参数失败,则将失败值传递给函数宏,该函数宏可能会捕获它并返回一些非失败结果。
letfun f(x1:t1 [or fail],...,xj:tj [or fail])=M.
- 宏机制的应用:非对称加密
type skey.
type pkey.
type coins.
(*格式:fun 函数名(参赛类型):输出参数的类型*)
fun pk(skey):pkey. (*公钥生成*)
fun internal_aenc(bitstring,pkey,coins):bitstring. (*加密函数*)
reduc
forall m:bitstring,k:skey,r:coins; (*参数名:类型*)
adec(internal_aenc(m,pk(k),r),k)=m. (*析构函数:解密函数*)
(*宏:每次加密时必须重新选择随机硬币r,为了避免在每次加密时都编写这段代码,我们可以定义一个函数宏aenc。*)
letfun aenc(x:bitstring,y:pkey)=new r:coins;intternal_aenc(x,y,r).
好消息:官方手册中明确表明,由于为加密原语定义正确的模型是困难的,我们建议重用现有的定义,例如本手册中给出的定义。
因此,我将手册中直接给出的密码原语建模列出来,并且我将用图文对相应的加密操作进行原理解释。
一、对称加密
和上一篇proverif语法介绍给出的对称加密不同之处在于,本代码使用了概率生成密钥进而形成加密函数internal_senc() :
type key.
type coins.
fun internal_senc(bitstring,key,coins):bitstring.
reduc
forall m:bitstring,k:key;
sdnc(internal_senc(m,k,r),k)=m.
(*宏:重定义函数。格式:letfun 函数名称(参数名称:类型)=new 参数名称:类型;构造函数(参数名称)*)
letfun senc(x:bitstring,y:key)=new r:coins;internal_senc(x,y,r).
二、非对称加密
于宏机制的应用中给出的非对称加密编码不同的是,下面的代码使用概率种子seed生成密钥对。
type seed.
type pkey.
type skey.
fun pk(seed):pkey.
fun sk(seed):skey.
fun aenc(bitstring,pkey):bitstring.
reduc
forall m:bitstring,k:seed;
adec(aenc(m,pk(k)),sk(k))=m.
三、Diffie-Hellman密钥协议
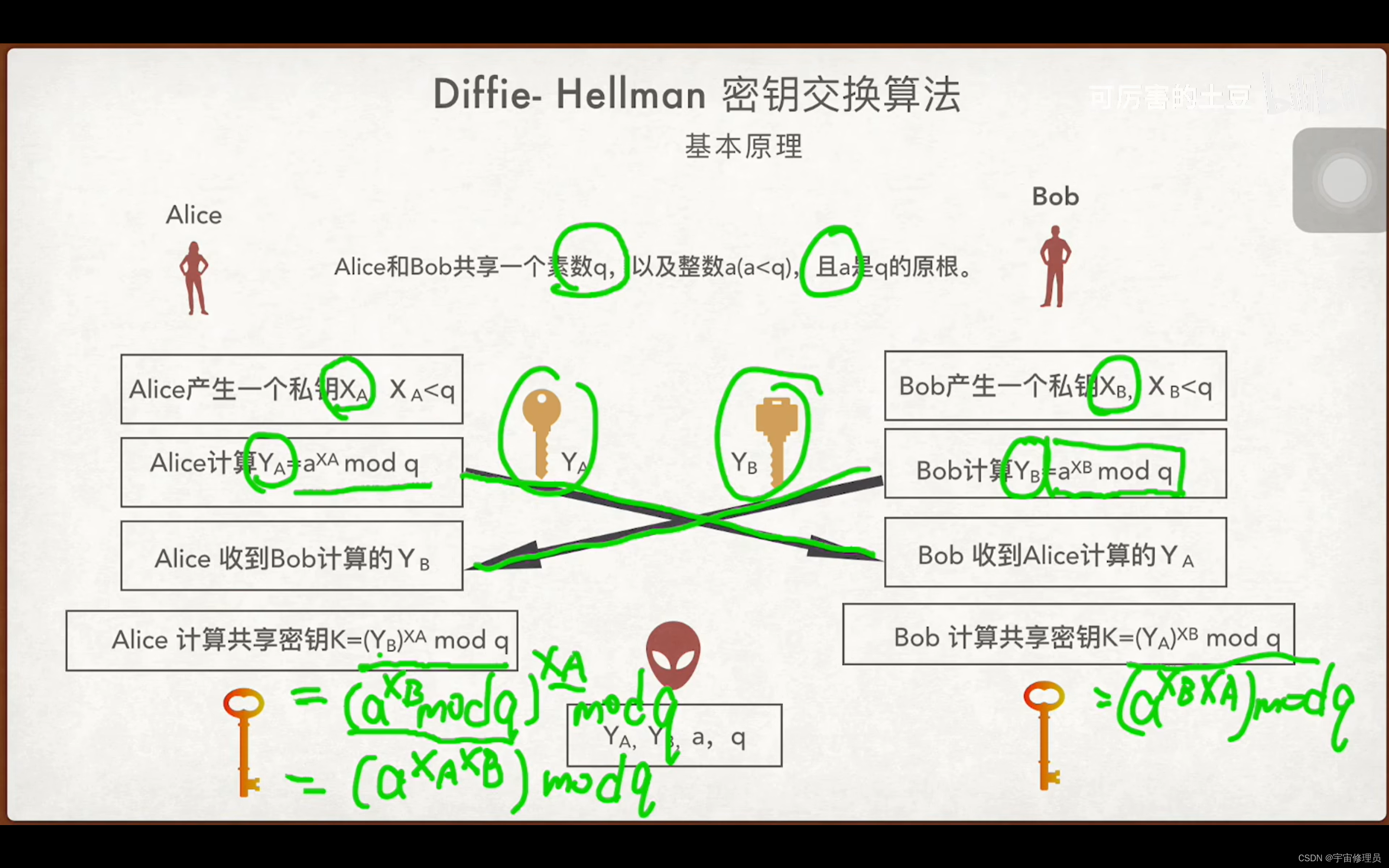
原理:DH算法的基本原理就是通过共享的参数协商一个对称秘钥,然后用这个对称秘钥加密后面的通信。这里用到了离散对数函数,这样即使中间人截获了公钥,也无法计算出各自的私钥。具体的公式如官网描述所示:

建模代码:
(*声明类型*)
type G.
type exponent. (*指数类型*)
(*定义常量g是G类型的数组*)
const g:G[data].
fun exp(G,exponent):G.(*G的exponent次方*)
equation forall x:exponent,y:exponent;exp(exp(g,x),y)=exp(exp(g,y),x).
四、HASH function
(*Hash func*)
fun h(bitstring):bitstring.
五、数字签名
原理:签名方用自己的私钥签名,验证方用签名方的公钥验证。


分两种:
5.1 带消息恢复的签名
(* Digital signatures *)
type sskey.
type spkey.
fun spk(sskey): spkey. (*公钥生成函数*)
fun sign(bitstring, sskey): bitstring. (*私钥签名*)
(*不需要私钥就可以将签名的信息恢复成明文*)
reduc forall m: bitstring, ssk: sskey; getmess(sign(m,ssk)) = m.
(*通过公钥进行验证sign*)
reduc forall m: bitstring, ssk: sskey; checksign(sign(m,ssk),spk(ssk)) = m.
5.2 带消息恢复的概率签名
(* Digital signatures *)
type sskey.
type spkey.
type scoins.
fun spk(sskey): spkey. (*公钥生成函数*)
fun internal_sign(bitstring, sskey,scoins): bitstring. (*概率性私钥签名*)
(*不需要私钥就可以将签名的信息恢复成明文*)
reduc
forall m: bitstring, k: sskey,r:scoins;
getmess(internal_sign(m,k,r)) = m.
reduc
forall m: bitstring, k: sskey,r: scions;
checksign(internal_sign(m,k,r),spk(k)) = m. (*通过公钥进行验证sign*)
(*宏定义:每次使用签名的时候都要新建一个概率,避免重复编写,使用宏定义。*)
letfun sign(m:bitstring,k:sskey)=new r:scoins;internal_sign(m,k,r).
六、消息验证码(MAC)
工作原理:
消息认证码的输入为任意长度的消息和一个发送者与接收者之间共享的密钥,它可以输出固定长度的数据,这个数据称为MAC 值。根据任意长度的消息输出固定长度的数据,这一点和单向散列函数很类似。但由于计算 MAC 值必须持有共享密钥,没有共享密钥的人就无法计算 MAC 值,因此消息认证码利用这一性质来完成认证。
此外,消息认证码和单向散列函数一样具有雪崩效应,哪怕消息中发生 1 比特的变化,也会导致 MAC 值发生不可区分的改变。
扩展:基于哈希的消息认证代码(HMAC)
一种消息认证代码,它使用加密哈希函数创建消息的摘要(或“消息认证代码”)。摘要可用于验证消息的真实性。HMAC是一种MAC,除了消息外,还使用密钥来生成摘要。
详细讲解:消息认证码(MAC)_简书
type mkey.
fun mac(bitstring,mkey):bitstring.
总结
提示:这里对文章进行总结:
例如:以上就是今天要讲的内容,本文仅仅简单介绍了pandas的使用,而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。