发现更多计算机知识,欢迎访问Cr不是铬的个人网站
最近数据结构学到二叉树,就刷了刷力扣,写这篇文章也是辅助记忆。
103二叉树锯齿形遍历

要解出本道题,首先要会层次遍历。层次遍历我们都知道用一个队列去实现就行。但是力扣这里的输出时一个二维的vector,每一层的值在不同的列表里面。这里是一个难点。这个锯齿形遍历无非加一个判断本层是奇数还是偶数层,然后用内置的revers函数处理一下就可。
代码:
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> ret; // 存储结果的二维向量
queue<TreeNode*> dq; // 辅助队列用于层序遍历
if (root == nullptr) {
return ret; // 如果根节点为空,直接返回空结果
}
dq.push(root); // 将根节点入队
int level = 1; // 层级标志,初始为1
while (!dq.empty()) {
int size = dq.size(); // 当前层的节点数
vector<int> tmp; // 临时向量存储当前层的节点值
for (int i = 0; i < size; i++) {
TreeNode* node = dq.front(); // 取出队首节点
dq.pop(); // 出队
tmp.push_back(node->val); // 将节点值存入临时向量
if (node->left != nullptr) {
dq.push(node->left); // 左子节点入队
}
if (node->right != nullptr) {
dq.push(node->right); // 右子节点入队
}
}
if (level % 2 == 0) {
reverse(tmp.begin(), tmp.end()); // 如果是偶数层级,将临时向量反转
}
ret.push_back(tmp); // 将当前层的节点值向量存入结果向量
level++; // 层级标志自增
}
return ret; // 返回结果向量
}
};103对称二叉树
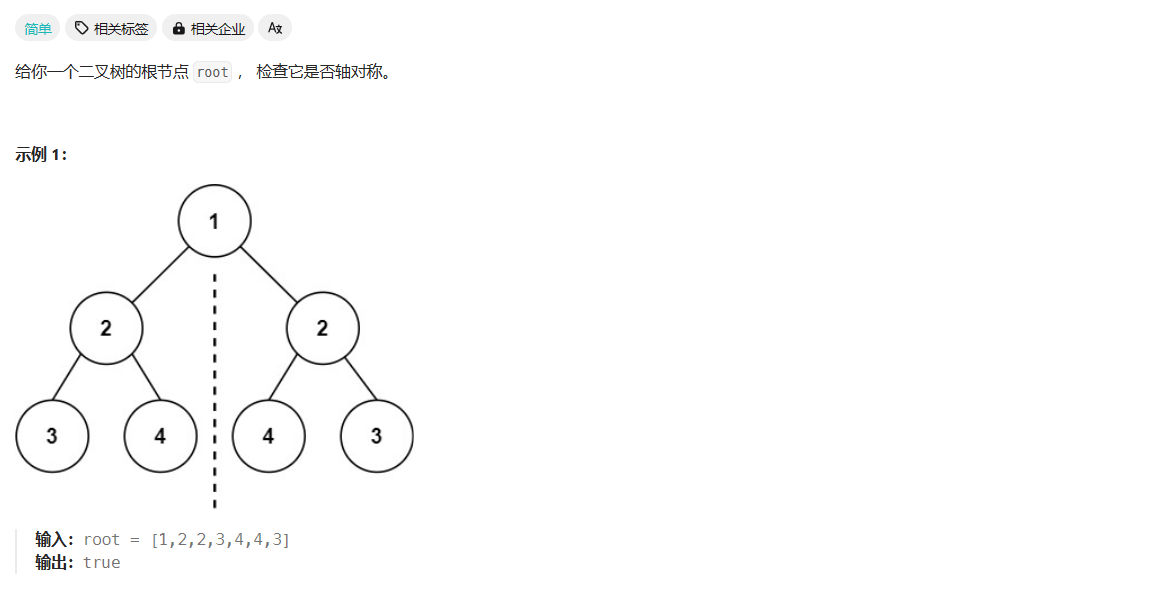
判断对称二叉树可以在判断完全相同的二叉树的基础上面进行。只是递归的时候变成了left->right ,rigth->left这种.
利用递归解决代码:
class Solution {
public:
// 判断两个节点是否镜像对称
bool isMirror(TreeNode* left, TreeNode* right) {
if (left == nullptr && right == nullptr) {
return true; // 如果两个节点都为空,则它们镜像对称
} else if (left == nullptr || right == nullptr) {
return false; // 如果其中一个节点为空,则它们不镜像对称
} else {
// 判断当前节点的值相等,并且左子树的左子节点与右子树的右子节点镜像对称,
// 左子树的右子节点与右子树的左子节点镜像对称
return (left->val == right->val) && isMirror(left->left, right->right) && isMirror(left->right, right->left);
}
}
// 判断二叉树是否对称
bool isSymmetric(TreeNode* root) {
if (root == nullptr) {
return true; // 如果根节点为空,则认为是对称的
}
return isMirror(root->left, root->right); // 判断根节点的左子树和右子树是否镜像对称
}
};在
isMirror函数中,如果两个节点都为空,则它们镜像对称;如果其中一个节点为空,则它们不镜像对称;否则,判断当前节点的值相等,并且左子树的左子节点与右子树的右子节点镜像对称,左子树的右子节点与右子树的左子节点镜像对称
由前序遍历与中序遍历得到树

这是一个非常经典的问题,这里我给出一个我觉得很容易理解的代码:
class Solution {
public:
// 通过前序遍历和中序遍历构建二叉树的递归函数
TreeNode* build(vector<int>& preorder, int l1, int r1, vector<int>& inorder, int l2, int r2) {
TreeNode* root = new TreeNode(preorder[l1]); // 创建当前子树的根节点
int i = l2;
while (inorder[i] != root->val) {
i++; // 在中序遍历中找到根节点的位置
}
int Llen = i - l2; // 计算左子树的长度
int Rlen = r2 - i; // 计算右子树的长度
if (Llen <= 0) {
root->left = nullptr; // 如果左子树长度小于等于0,说明左子树为空
} else {
// 递归构建左子树,左子树的前序遍历范围为[l1+1, l1+Llen],中序遍历范围为[l2, i-1]
root->left = build(preorder, l1 + 1, l1 + Llen, inorder, l2, i - 1);
}
if (Rlen <= 0) {
root->right = nullptr; // 如果右子树长度小于等于0,说明右子树为空
} else {
// 递归构建右子树,右子树的前序遍历范围为[l1+Llen+1, r1],中序遍历范围为[i+1, r2]
root->right = build(preorder, l1 + Llen + 1, r1, inorder, i + 1, r2);
}
return root; // 返回当前子树的根节点
}
// 构建二叉树
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int n = preorder.size(); // 前序遍历序列的长度
int m = inorder.size(); // 中序遍历序列的长度
TreeNode* root;
root = build(preorder, 0, n - 1, inorder, 0, m - 1); // 调用递归函数构建二叉树
return root; // 返回根节点
}
};考虑一下,如果要求的是从后序遍历和中序遍历得到树呢?上述代码该如何变化呢?
这里也贴上代码:
class Solution {
public:
TreeNode* build(vector<int>& inorder, int l1, int r1, vector<int>& postorder, int l2, int r2)
{
if (l1 > r1 || l2 > r2)
return nullptr;
TreeNode* root = new TreeNode(postorder[r2]);
int i = l1;
while (inorder[i] != root->val)
i++;
int Llen = i - l1;
int Rlen = r1 - i;
root->left = build(inorder, l1, i - 1, postorder, l2, l2 + Llen - 1);
root->right = build(inorder, i + 1, r1, postorder, l2 + Llen, r2 - 1);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int n = inorder.size();
int m = postorder.size();
TreeNode* root;
root = build(inorder, 0, n - 1, postorder, 0, m - 1);
return root;
}
};本文由博客一文多发平台 OpenWrite 发布!