文章链接:Federated Learning of a Mixture of Global and Local Models
发表期刊(会议): ICLR 2021 Conference(机器学习顶会)
往期博客:FLMix: 联邦学习新范式——局部和全局的结合
目录
- 1.背景介绍
- 2. 梯度下降 GD
- SGD
- LGD
- 3. L2GD
- L2GD创设
- 局部GD和平均局部模型
- L2GD 通信
- L2GD收敛证明
- L2SGD+
1.背景介绍
本文提出了一种新的训练联邦学习模型的优化公式。标准FL旨在从存储在所有参与设备上的私人数据中找到一个单一的全局模型。相比之下,新方法寻求全局模型和局部模型之间的权衡,每个设备可以从自己的私有数据中学习而无需通信。
本文开发了有效的随机梯度下降(SGD)变体来求解新公式,并证明了通信复杂性的保证。该工作的主要贡献包括结合全局和局部模型的FL新范式、新范式的理论性质、无环路局部梯度下降(L2GD)、L2GD的收敛理论以及对局部步骤在联邦学习中的作用的见解。该文件还强调了本地SGD在通信复杂性和个性化联邦学习的好处方面优于传统SGD的潜力。
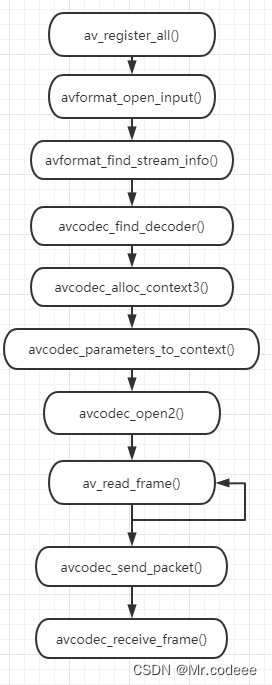
2. 梯度下降 GD
梯度下降(Gradient Descent,GD)是一种常用的优化算法,用于最小化损失函数或目标函数。基本思想是通过迭代更新模型参数的方式来寻找使目标函数达到最小值的参数值。
GD通过沿着损失函数的负梯度方向来更新模型参数,以减少损失并使模型更符合训练数据。
GD基本步骤:
- 初始化参数:选择初始的模型参数值,随机初始化或根据先验知识设置。
- 计算梯度:在当前参数值处,计算目标函数关于参数的梯度(即目标函数对参数的偏导数)。梯度表示了目标函数在当前参数值处的变化方向和速率。
- 更新参数:根据梯度信息和学习率(learning rate),更新模型参数。学习率决定了每次迭代中参数更新的步长大小。更新规则通常如下所示:
新参数=旧参数−学习率×梯度- 重复迭代:重复步骤 2 和步骤 3,直到满足停止条件,例如达到最大迭代次数、损失函数收敛等。
学习率是一个很重要的超参,制着在每次迭代中更新参数的幅度。它决定了在梯度方向上参数更新的步长大小。
学习率过大可能导致参数更新过大,甚至可能使得优化算法无法收敛,造成震荡或发散。这种情况下,即使损失函数值在短时间内降低,最终可能错过最优解。
学习率过小则可能导致收敛速度缓慢,需要更多的迭代次数才能达到一个较好的解,特别是在损失函数的优化路径中存在较为平缓的部分时。
SGD
随机梯度下降(Stochastic Gradient Descent,SGD)是一种常用的优化算法,用于训练ML模型,特别是在大规模数据集上。它是GD算法的一种变体,使用单个样本或样本小批次(mini-batch)的梯度估计来进行参数更新,而不是使用整个训练集的梯度。这种随机性使得随机梯度下降在大型数据集上更具效率,并且能够更快地收敛到局部最优解。
优点:
- 在大规模数据集上的训练更加高效
- 易于实现
缺点:
- 可能陷入局部最优解
- 对学习率敏感
function stochastic_gradient_descent(data, learning_rate, num_epochs):
initialize random parameters theta
for epoch in range(num_epochs):
shuffle(data) # Shuffle the data for randomness
for example in data:
input_x, target_y = example
# 计算损失函数梯度值
gradient = compute_gradient(input_x, target_y, theta)
# 使用梯度下降更新参数
for param in theta:
param -= learning_rate * gradient[param]
return theta
LGD
分层梯度下降(Layer-wise Gradient Descent,LGD)是一种用于深度学习中神经网络训练的优化算法。它的主要思想是将神经网络分层,然后对每一层分别进行训练和更新。这种方法旨在解决深度神经网络训练中的梯度消失或梯度爆炸等问题,并提高网络训练的效率。
与SGD的比较
| SGD | LGD | |
|---|---|---|
| 分层更新 | 每次迭代中使用整个网络的梯度来更新参数 | 对每一层单独计算和更新梯度 |
| 更新频率 | 每次迭代中更新整个网络的参数 | 按层级顺序逐层更新参数,网络参数的更新频率较低 |
| 梯度传播 | 传播通过所有层来更新参数 容易出现梯度消失或梯度爆炸 | 通过分层的方式减少了参数更新时的梯度传播距离 有助于缓解梯度问题 |
| 收敛速度 | 由于同时更新所有参数 需要较长时间才能收敛到较优解 | 通过分层更新 会更快地收敛到局部最优解 |
function layer_wise_gradient_descent(network, data, learning_rate, num_epochs):
initialize random parameters for each layer in network
for epoch in range(num_epochs):
shuffle(data) # Shuffle the data for randomness
for example in data:
input_x, target_y = example
# Forward pass through the network
predictions = network.forward_pass(input_x)
# Backward pass to compute gradients for each layer
network.compute_gradients(input_x, target_y)
# Update parameters of each layer using gradients
for layer in network.layers:
layer.update_parameters(learning_rate)
return network
3. L2GD
文章提出了联邦学习新范式 ♣ \clubsuit ♣ 如下:
♣ min x 1 , . . . , x n ∈ R d { F ( x ) : = f ( x ) + λ ψ ( x ) } f ( x ) : = 1 n ∑ i = 1 n f i ( x i ) ψ ( x ) : = 1 2 n ∑ i = 1 n ∥ x i − x ‾ ∥ 2 \clubsuit \quad \min_{x_1,...,x_n \in \mathbb{R}^d } \{ F(x): = f(x)+ \lambda \psi (x)\} \\ f(x):=\frac{1}{n}\sum_{i=1}^{n} f_i(x_i) \\ \psi (x) := \frac{1}{2n}\sum_{i=1}^{n} \left \| x_i-\overline{x} \right \| ^2 ♣x1,...,xn∈Rdmin{F(x):=f(x)+λψ(x)}f(x):=n1i=1∑nfi(xi)ψ(x):=2n1i=1∑n∥xi−x∥2 其中 λ ≥ 0 \lambda \ge0 λ≥0 是一个惩罚超参, x 1 , . . . , x n ∈ R d x_1,...,x_n \in \mathbb{R}^d x1,...,xn∈Rd 是本地模型参数 , x : = ( x 1 , x 2 , . . . , x n ) ∈ R n d x:=(x_1,x_2,...,x_n) \in\mathbb{R}^{nd} x:=(x1,x2,...,xn)∈Rnd 并且 x ‾ : = 1 n ∑ i = 1 n x i \overline{x}:=\frac{1}{n}\sum_{i=1}^{n}x_i x:=n1∑i=1nxi 是所有本地模型的平均值。
本文设计了一种新的随机化方法Loopless Local GD (L2GD)来求解范式 ♣ \clubsuit ♣
L2GD创设
L2GD方法是一个非一致的SDG,可以视为一个2元和问题,通过随机采样
∇
f
\nabla f
∇f 或者
∇
ψ
\nabla \psi
∇ψ 来估计
∇
F
\nabla F
∇F。
令采样概率为 P ∈ ( 0 , 1 ) P \in(0,1) P∈(0,1),对于 F F F 在 x ∈ R n d x \in \mathbb{R}^{nd} x∈Rnd 的随机梯度可表示为: G ( x ) : = { ∇ f ( x ) 1 − p w i t h p r o b a b i l i t y 1 − p λ ∇ ψ ( x ) p w i t h p r o b a b i l i t y p G(x): = \begin{cases} \frac{\nabla f(x)}{1-p} & with\quad probability \quad 1 − p \\ \frac{\lambda \nabla \psi(x)}{p} & with\quad probability\quad p \\ \end{cases} G(x):={1−p∇f(x)pλ∇ψ(x)withprobability1−pwithprobabilityp其中 G ( x ) G(x) G(x) 是 ∇ F ( x ) \nabla F(x) ∇F(x) 的无偏估计。
使用L2GD以最小化
F
F
F :
♠
x
k
+
1
=
x
k
−
α
⋅
G
(
x
k
)
\spadesuit \quad x^{k+1}=x^k-\alpha \cdot G(x^k)
♠xk+1=xk−α⋅G(xk)
α
\alpha
α 为学习率或步长,将
G
(
x
)
G(x)
G(x) 代入
♠
\spadesuit
♠ 可以得到L2GD的更新算法:

在每一轮迭代中,会先抛一枚硬币
ξ
\xi
ξ :
-
如果 ξ = 1 \xi =1 ξ=1 则以概率 p \quad p \quad p 采样 ∇ ψ \nabla \psi ∇ψ 来估计 ∇ F \nabla F ∇F 并进行参数更新,此时 Master 将每个局部模型向平均值方向移动;
-
如果 ξ = 0 \xi =0 ξ=0 则以概率 1 − p 1-p 1−p 采样 ∇ f \nabla f ∇f 来估计 ∇ F \nabla F ∇F 并进行参数更新,此时所有设备执行一个局部GD步骤。
为了保证 ♡ x i k + 1 = ( 1 − α λ n p ) x i k + α λ n p x ˉ k \heartsuit \quad x^{k+1}_i=(1-\frac{\alpha \lambda}{np})x^k_i+\frac{\alpha \lambda}{np} \bar{x}^k ♡xik+1=(1−npαλ)xik+npαλxˉk 是一个关于 x i k x^k_i xik 和 x ˉ k \bar{x}^k xˉk 的凸组合,
需要对 α \alpha α 的大小进行限制,使 α λ n p < 1 2 \frac{\alpha \lambda}{np}<\frac{1}{2} npαλ<21。
在上述算法的基础上,只需要在连续两次投掷硬币得到不同 ξ \xi ξ 值时进行通信。
需要注意的是,算法语句没有考虑到数据的隐私。 而隐私是FL的一个非常重要的方面。
局部GD和平均局部模型
局部模型的平均值在聚合步骤中不会更改。具体表现为聚合后的
x
ˉ
k
+
1
\bar{x}^{k+1}
xˉk+1 具有以下性质(结合公式
♡
\heartsuit
♡):
x
ˉ
k
+
1
=
1
n
∑
i
=
1
n
x
i
k
+
1
=
1
n
∑
i
=
1
n
[
(
1
−
α
λ
n
p
)
x
i
k
+
α
λ
n
p
x
ˉ
k
]
=
x
ˉ
k
\bar{x}^{k+1}=\frac{1}{n} \sum_{i=1}^{n} x^{k+1}_i =\frac{1}{n}\sum_{i=1}^{n}[(1-\frac{\alpha \lambda}{np})x^k_i+\frac{\alpha \lambda}{np} \bar{x}^k]=\bar{x}^{k}
xˉk+1=n1i=1∑nxik+1=n1i=1∑n[(1−npαλ)xik+npαλxˉk]=xˉk这意味着如果在一个执行序列中发生了几个平均步骤,
♡
\heartsuit
♡ 中的点
a
=
x
ˉ
k
a=\bar{x}^k
a=xˉk 始终保持不变,每个局部模型
x
i
k
x_i^k
xik 只是在执行序列和
a
a
a 的开始处沿着连接局部模型初始值的直线移动,每一步都将
x
i
k
x^k_i
xik 向平均值 a 靠近。
至此,我们可以得到这样一个结论:
- 局部GD步骤越多,局部模型越接近纯局部模型
- 采取的平均步骤越多,局部模型就越接近它们的平均值。
局部GD与平均步骤的相对数量由参数 p p p 控制:
- 局部GD步骤的期望数量是 1 p \frac{1}{p} p1
- 平均步骤的期望数量是 1 1 − p \frac{1}{1-p} 1−p1
L2GD 通信

为了更好地理解算法中通信发生的时间,考虑以下可能的抛硬币顺序 :0,0,1,0,1,1,0。
-
前两次抛硬币 ( ξ = 0 ) (\xi =0) (ξ=0) 将导致在所有设备上执行两个局部GD步骤,第 i i i 台设备 的局部模型为 x i k = 2 x_i^{k=2} xik=2;
-
第三次掷硬币 ( ξ = 1 ) (\xi =1) (ξ=1),此时所有的局部模型 x i k = 2 x_i^{k=2} xik=2 都会被传送给 Master,取平均值形成 x ˉ k = 2 \bar{x}^{k=2} xˉk=2,然后就开始了取平均的步骤 ♡ \heartsuit ♡ 得到每台设备的新局部模型 x i k = 3 x_i^{k=3} xik=3
-
第四次掷硬币 ( ξ = 0 ) (\xi =0) (ξ=0),此时 Master 将更新的局部模型 x i k = 3 x_i^{k=3} xik=3 发送回设备 i i i,设备 i i i 随后执行一个局部GD步骤,得到 x i k = 4 x_i^{k=4} xik=4
-
然后是连续三次抛硬币 ( ξ = 1 ) (\xi =1) (ξ=1),这意味着局部模型再次被传递给 Master ,Master 执行三个平均步骤 ♡ \heartsuit ♡ 得到 x i k = 7 x_i^{k=7} xik=7
-
第八次掷硬币 ( ξ = 0 ) (\xi =0) (ξ=0),这使得 Master 将更新后的局部模型 x i k = 7 x_i^{k=7} xik=7 发送回设备 i i i,设备随后执行单个局部GD步骤,得到 x i k = 8 x_i^{k=8} xik=8。
这个例子说明了当两个连续的硬币投掷出不同的值时,需要进行通信:
- 如果0后面跟着一个1,那么所有的设备都与 Master 通信;
- 如果1后面跟着一个0,那么 Master 就返回给设备通信。
- 标准是将每对通信,Device→Master 和随后的 Master → Device,计数为单个通信轮。
- 在
L2GD的 k k k 个迭代中,预期的通信轮数为 p ( 1 − p ) k p(1−p)k p(1−p)k 。
L2GD收敛证明
本文在提出联邦学习新范式的时候做过一个重要的假设,可以参考前文:FLMix: 联邦学习新范式——局部和全局的结合。
对于每一个设备 i i i ,它的目标函数 f i : R d → R f_i:\mathbb{R}^d \rightarrow \mathbb{R} fi:Rd→R 是 L − s m o o t h L-smooth L−smooth 并且 μ − s t r o n g l y \mu -strongly μ−strongly 的凸函数。
用数学表示即为:
L
f
:
=
L
n
L_f:=\frac{L}{n}
Lf:=nL和
μ
f
:
=
μ
n
\mu_f:=\frac{\mu}{n}
μf:=nμ 那么对于函数
ψ
\psi
ψ ,显然它是凸的。并且有一下表达:
(
∇
ψ
(
x
)
)
i
=
1
n
(
x
i
−
x
ˉ
)
ψ
(
x
)
=
n
2
∑
i
=
1
n
∣
∣
(
(
∇
ψ
(
x
)
)
i
)
∣
∣
2
=
n
2
∣
∣
∇
ψ
(
x
)
∣
∣
2
(\nabla \psi(x))_i=\frac{1}{n}(x_i-\bar{x}) \\ \psi(x)=\frac{n}{2}\sum_{i=1}^{n}||((\nabla \psi(x))_i)|| ^2=\frac{n}{2}||\nabla \psi(x)||^2
(∇ψ(x))i=n1(xi−xˉ)ψ(x)=2ni=1∑n∣∣((∇ψ(x))i)∣∣2=2n∣∣∇ψ(x)∣∣2我们保持这个假设在L2DG的计算中仍然成立。
如果 学习率 α < 1 2 L \alpha<\frac{1}{2\mathcal{L} } α<2L1 其中 L : = 1 n max { L 1 − p , λ p } \mathcal{L} :=\frac{1}{n}\max\{\frac{L}{1-p},\frac{\lambda}{p}\} L:=n1max{1−pL,pλ} 有: E [ ∥ x k − x ( λ ) ∥ 2 ] ≤ ( 1 − α μ n ) k ∥ x 0 − x ( λ ) ∥ 2 + 2 n α σ 2 μ w h e r e σ 2 : = 1 n 2 ∑ i = 1 n ( 1 1 − p ∥ ∇ f i ( x i ( λ ) ) ∥ 2 + λ 2 p ∥ x i ( λ ) − x ˉ ( λ ) ∥ 2 ) \mathbb{E} \left [ \left \| x^k-x(\lambda) \right \|^2 \right ] \le(1-\frac{\alpha \mu}{n})^k\left \| x^0-x(\lambda) \right \|^2+\frac{2n\alpha \sigma^2 }{\mu} \\ \\ where \quad \quad \sigma^2:=\frac{1}{n^2}\sum_{i=1}^{n}(\frac{1}{1-p}\left \| \nabla f_i(x_i(\lambda)) \right \|^2 +\frac{\lambda^2}{p}\left \| x_i(\lambda)-\bar{x}(\lambda) \right \|^2 ) E[ xk−x(λ) 2]≤(1−nαμ)k x0−x(λ) 2+μ2nασ2whereσ2:=n21i=1∑n(1−p1∥∇fi(xi(λ))∥2+pλ2∥xi(λ)−xˉ(λ)∥2)我们需要找到超参 p , α p,α p,α,使得函数能以最快的速率以将误差收敛到最优值的 ( O ( ε ) + 2 n α σ 2 μ ) (\mathcal{O}(\varepsilon )+\frac{2n\alpha\sigma^2}{\mu}) (O(ε)+μ2nασ2) 邻域内,也就是说,实现 ♯ E [ ∥ x k − x ( λ ) ∥ 2 ] ≤ ε ∥ x 0 − x ( λ ) ∥ 2 + 2 n α σ 2 μ \sharp \quad \mathbb{E} \left [ \left \| x^k-x(\lambda) \right \|^2 \right ] \le\varepsilon\left \| x^0-x(\lambda) \right \|^2+\frac{2n\alpha \sigma^2 }{\mu} ♯E[ xk−x(λ) 2]≤ε x0−x(λ) 2+μ2nασ2 推论:当值 p ∗ = λ L + λ p^* =\frac{ λ}{ L+λ} p∗=L+λλ 时,可以令迭代次数和实现 ♯ \sharp ♯ 的预期通信次数两者最小化。
特别地,最佳迭代次数是 2 L + λ μ l o g 1 ε 2\frac{L+\lambda}{ \mu} log\frac{ 1}{\varepsilon} 2μL+λlogε1,并且最佳预期通信次数是 2 λ λ + L L μ l o g 1 ε \frac{2λ}{ λ+L}\frac{ L}{ \mu} log \frac{1}{ ε} λ+L2λμLlogε1。
如果令 p = p ∗ p=p^* p=p∗ 那么 α λ n p = 1 2 \frac{\alpha \lambda}{np}=\frac{1}{2} npαλ=21,并且算法1中的 ♡ \heartsuit ♡ 简化为: x i k = 1 2 ( x i k + x ˉ k ) x_i^k=\frac{1}{2}(x_i^k +\bar{x}^k) xik=21(xik+xˉk)并且局部GD的更新步骤简化为: x i k + 1 = x i k − 1 2 L ∇ f i ( x i k ) x_i^{k+1}=x_i^k-\frac{1}{2L}\nabla f_i(x_i^k) xik+1=xik−2L1∇fi(xik)对于简化后的两个式子,有以下几点发现:
- 虽然本文提出的方法不支持完全平均,因为它太不稳定,但推论表明应该向平均迈出一大步。
- 随着 λ \lambda λ 变小,优化问题 ♣ \clubsuit ♣ 的解将越来越倾向于纯局部模型,即当 λ → 0 λ → 0 λ→0 有 x i ( λ ) → x i ( 0 ) : = a r g min f i x_i(\lambda)→ x_i(0):= arg \min f_i xi(λ)→xi(0):=argminfi。纯局部模型可以在没有任何通信的情况下计算。
L2SGD+
L2GD是SGD的一个特定实例,因此它只线性收敛到一个最优邻域。这意味着,它只能求解具有凸函数性质的优化目标,当函数存在非凸(有局部最优解)区域时,L2GD可能会陷入凹区域。
为了解决上述问题,作者提出将控制变量纳入随机梯度,进一步假设每个局部目标都具有有限和结构,并提出了L2SGD+算法。
假设 f i f_i fi 有个有限和结构: f i ( x i ) = 1 m ∑ j = 1 m f i , j ′ ( x i ) f_i(x_i)=\frac{1}{m}\sum_{j=1}^{m}f_{i,j}'(x_i) fi(xi)=m1j=1∑mfi,j′(xi)令 f i , j ′ f_{i,j}' fi,j′ 强凸且 L − s m o o t h L-smooth L−smooth , 同时 f i f_i fi 是 μ − s t r o n g l y \mu-strongly μ−strongly 凸函数。
篇幅有限,加之本人能力有限,这边就不展开讲解了,有兴趣的同仁可以去看原文的推导证明,还挺有挑战的。