二、对偶理论与灵敏度分析
用矩阵形式表示原问题和对偶问题: max z = C X s . t . { A X ≤ b X ≥ 0 \max z=\pmb{CX}\\ s.t.\begin{cases} \pmb{AX\leq b} \\ \pmb{X}\geq\pmb{0} \end{cases} maxz=CXs.t.{AX≤bX≥0 其中 C = ( c 1 , c 2 , ⋯ , c n ) , X = ( x 1 , x 2 , ⋯ , x n ) T , A m × n , b = ( b 1 , b 2 , ⋯ , b m ) T \pmb{C}=(c_1,c_2,\cdots,c_n),\pmb{X}=(x_1,x_2,\cdots,x_n)^T,\pmb{A}_{m\times n},\pmb{b}=(b_1,b_2,\cdots,b_m)^T C=(c1,c2,⋯,cn),X=(x1,x2,⋯,xn)T,Am×n,b=(b1,b2,⋯,bm)T 。
其对偶问题为: min w = Y b s . t . { A T Y T ≥ C T Y T ≥ 0 \min w=\pmb{Yb}\\ s.t.\begin{cases} \pmb{A^TY^T\geq C^T} \\ \pmb{Y^T}\geq\pmb{0} \end{cases} minw=Ybs.t.{ATYT≥CTYT≥0 其中 Y = ( y 1 , y 2 , ⋯ , y m ) \pmb{Y}=(y_1,y_2,\cdots,y_m) Y=(y1,y2,⋯,ym) 。
对偶理论的几个定理:
弱对偶定理: 若互为对偶问题的线性规划问题分别有可行解 X , Y \pmb{X},\pmb{Y} X,Y ,则原问题的目标函数值不大于对偶问题的目标函数值。
有推论:若原问题可行,则其目标函数无界的充要条件为对偶问题没有可行解。
最优准则性定理: 当 C X = Y b \pmb{CX=Yb} CX=Yb 时,两个问题均达到最优。
对偶定理: 若原问题有最优解,则对偶问题也有最优解,且目标函数值相同。
互补松弛定理: 若 X ‾ , Y ‾ \pmb{\overline{X},\overline{Y}} X,Y 分别为原问题和对偶问题的可行解,那么当且仅当 X ‾ , Y ‾ \pmb{\overline{X},\overline{Y}} X,Y 为最优解时,有 Y ‾ X s = 0 , X ‾ Y s = 0 \pmb{\overline{Y}X_s=0,\overline{X}Y_s=0} YXs=0,XYs=0 ,其中 X s , Y s \pmb{X_s,Y_s} Xs,Ys 分别为对应线性规划问题添加的松弛变量所构成的向量。
当原问题的最优解 X \pmb{X} X 非零时,对偶问题添加的松弛变量一定为 0 ,也就是说对偶问题的约束条件是等式约束。同理,对偶问题的最优解非零时,原问题的约束条件就取严格等式。
需要注意的情况是,当原问题某个最优解取值为 0 时,不能说明对偶问题对应的约束就是等式,因为其是非等式时,即 Y s ≠ 0 Y_s\ne0 Ys=0 ,还是有 X Y s = 0 XY_s=0 XYs=0 。
对偶问题的经济解释 —— 影子价格。对偶问题的最优解所代表的就是单位资源对企业的价值,也就是资源所对应的影子价格。一般用增加一个单位该资源来描述,即若某资源的影子价格为 k k k ,若增加一个单位该资源,最优目标函数值增加 k k k 。不过,不能说增加 5 个单位,目标函数就增加 5 k 5k 5k ,因为,如果加了超过 1 个单位资源的话,有可能最优解就改变了。
对偶理论一个应用就是,原问题最优单纯形表中,松弛变量所对应的 z j z_j zj 就是对偶问题的最优解,即影子价格。
若 B \pmb{B} B 是 A \pmb{A} A 中的一个基,当 B \pmb{B} B 对应的基解是可行解时,称 B \pmb{B} B 为可行基,当 B \pmb{B} B 对应的基本可行解为最优解时,称 B \pmb{B} B 为最优基。若 C B − 1 \pmb{CB}^{-1} CB−1 是对偶问题的可行解,则称 B \pmb{B} B 为对偶可行基。
B \pmb{B} B 是线性规划问题的最优基的充要条件是, B \pmb{B} B 是可行基,同时是对偶可行基。在单纯形法中,我们从一个初始基可行解出发(假设还未达到最优解),它保证了原问题可行,却并未保证对偶问题可行。对偶问题可行需要 Y \pmb{Y} Y 非负,对应于原问题单纯形表中就是非基变量的 z j ≥ 0 z_j\geq0 zj≥0 ,那检验数就应该是小于等于 0 的。因此,只有原问题达到了最优解,即检验数都小于等于 0 ,对偶问题才是可行的。
因此,我们可以对称考虑,就是,先让对偶问题可行(原问题就最优),通过不断迭代,使得对偶问题最优(原问题就可行)。对偶单纯形法应用的前提便是,需要初始单纯形表中的检验数行全部非正(保证了原问题最优,也就是对偶问题可行)和基变量取值有负值(原问题不可行)。
对偶单纯形法的步骤为:
- 求一个满足最优性检验的初始基本解,列表;
- 若所有右端系数均非负,则已找到最优解,否则转下一步;
- 求另一个满足最优性检验且更接近可行解的基本解。换出变量原则,非可行中最小者,即 min { b i ∣ b i < 0 } \min\{b_i|b_i<0\} min{bi∣bi<0} ;换入原则,最小比例原则,检验数除以负的 a l k a_{lk} alk 最小者对应的非基变量。
灵敏度分析首先需要明白,我这一个参数变化,会影响最优单纯形表中的哪些数字。因此就要求我们掌握最优单纯形表的特征。
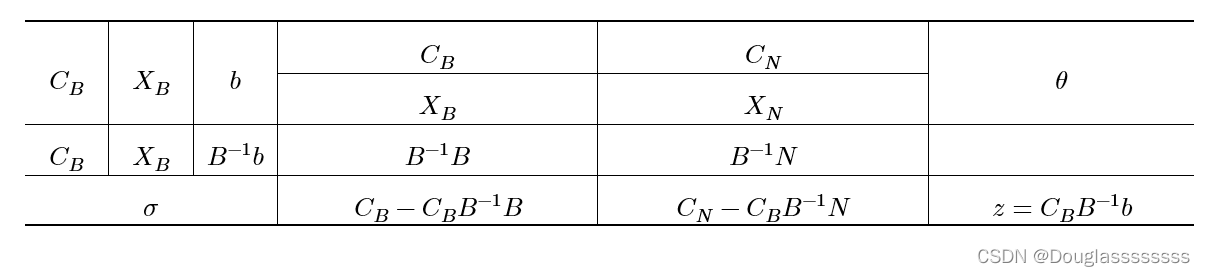
对于目标函数系数
c
j
c_j
cj ,如果它是基变量对应的系数,那么,它会影响所有非基变量的检验数;如果它是非基变量对应的系数,那么它的变化只会改变该非基变量的检验数。对于右端列向量
b
b
b ,它的变化会引起最终最优解的取值。对于约束系数
a
i
j
a_{ij}
aij ,如果它对应的变量为非基变量,它的变化只会影响该非基变量的检验数;如果它对应的变量为基变量,会影响
B
−
1
\pmb{B}^{-1}
B−1 ,则不仅右端常数变化,所有非基变量检验数都发生变化。
知道了这些变化在最优单纯形表中的反映,我们就不用记忆书上的公式,统统用待定系数法。
对于新增加变量的情况,我们可以先用 B − 1 \pmb{B}^{-1} B−1 去求它在最优单纯形表中的系数列向量,进而求出检验数,如果是非正,那就不会改变最优解;而如果是正数,说明把这个新变量加进来对目标有益,因此把它作为基变量继续迭代。
对于添加了约束的情况,首先看看原来的最优解是不是满足这个约束,如果也满足,那最优解就不变;如果不满足,把这个约束添加松弛变量化成等式,直接添加到最优单纯形表中,并将其添加的松弛变量作为基变量继续迭代。