---

算法效率

算法效率分析分为两种:第一种是时间效率，第二种是空间效率。时间效率被称为时间复杂度，而空间效率被称作空间复杂度。时间复杂度主要衡量的是一个算法的运行速度，而空间复杂度主要衡量一个算法所需要的额外空间，在计算机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展，计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。

时间复杂度

概念

在计算机科学中，算法的是时间复杂度是一个函数，它定量的描述了该算法运行的时间，但是理论上是不能够算出来的，因为同一个算法在不同机器上的运行时间是不一样的，这取决于机器的效率。又因为一个算法花费的时间和和语句的执行次数成正比，所以我们可以通过算执行次数来代替算时间。也就是说算法中基本操作的执行次数即时间复杂度。

计算

实际中我们计算时间复杂度时，我们其实并不一定要计算精确的执行次数，而只需要大概执行次数，那么这里我们使用大0的渐进表示法
大0符号(Big O notation):是用于描述函数渐进行为的数学符号。推导大0阶方法:
1、用常数1取代运行时间中的所有加法常数，即常数次数都用O（1)表示.
2、在修改后的运行次数函数中，只保留最高阶项，如：N^2+N+4>>O(N ^2)
3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大0阶,如：2N>>O(N)
4、有n次和常数次时常数次舍掉如：N+3>>O(N)

例1

简单循环
代码：

上面代码中一共执行了 5+3=8次，根据大O渐进法来说所有的常数都表示为O（1）.
所以这个代码的时间复杂度为O（1）.

例2

还是举个简单的例子来计算
代码：
上面的代码一共执行了n+5次
根据大O渐进法来说这里的 5 舍掉，所以这里的时间复杂度为O（n）

例3

冒泡排序（不懂的话可以看我主页哦，有详解）

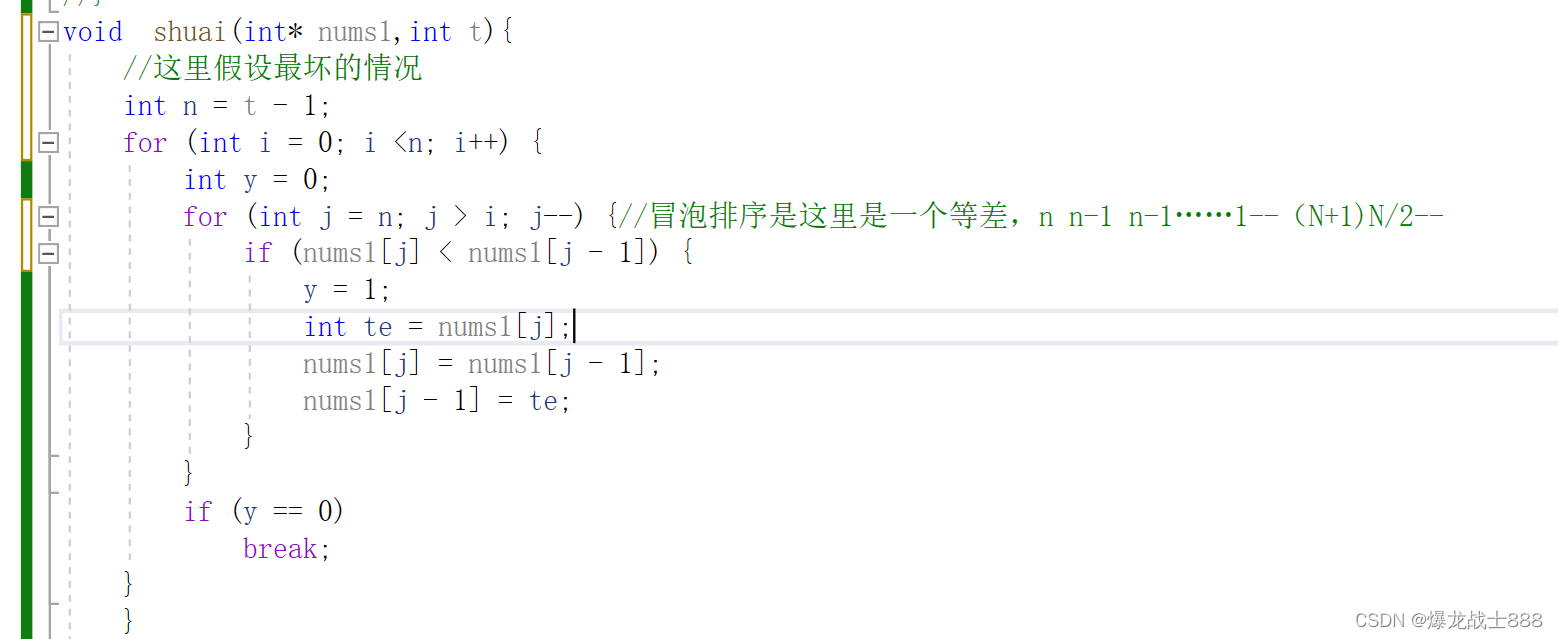
冒泡排序是这里是一个等差数列，n n-1 n-1……1–（N+1)N/2=(N*N-N)/2，根据大O渐进法来说这里的1/2，和N都要舍掉
所以这里的时间复杂度为O（N^2）

补充

例4

二分查找法（不懂的话可以看我主页哦，有详解）

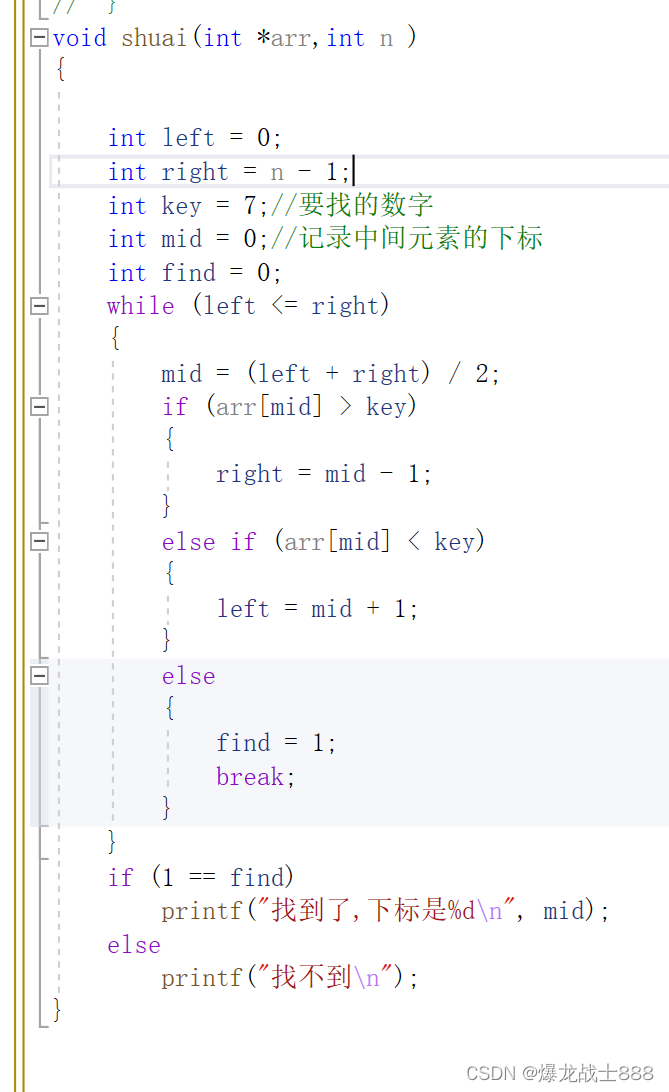
二分查找每查找一次都折一半，那我们将过程反过来列式 >>相当于每找一次就乘2 222*2=n,**假设查找x次>>2^x=n>>lon2N（这里2为底）也可以写成lonN
所以二分查找法的时间复杂度为O（lonN）**

有的童鞋说是不是一层循环时间复杂度就是O（n），两层就是O（N^2）捏，其实这是错的

从二分查找法就可以看出，二分查找有一层循环但是时间复杂度不为O(n)
这是要具体分析算法才能得出的

空间复杂度

空间复杂度的概念：空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度，空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是额外变量的个数。空间复杂度计算规则基本跟时间复杂度类似，也使用大0渐进表示法。
还有一个点是空间是可以重复利用的

例1

给数组赋值

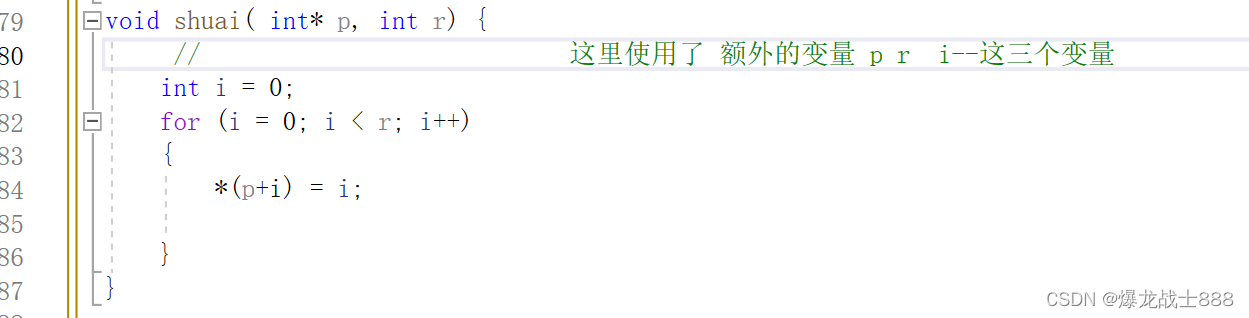
这里用了三个额外的变量p（指针变量），i，r，再根据大O渐进法来讲常数都用O（1）表示
所以这里的空间复杂度为O（1）；

例2

交换数组

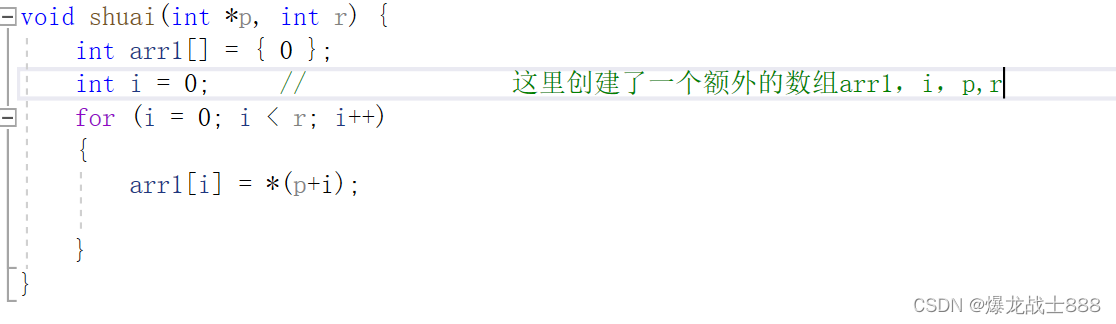
这里创建额外的数组用了n个空间，还有i，r，p（指针变量）三个变量，一共n+3，
根据大O渐进法这里的空间复杂度为O（n）。