相关关系与因果关系

本文来自：https://towardsdatascience.com/a-step-by-step-guide-in-detecting-causal-relationships-using-bayesian-structure-learning-in-python-c20c6b31cee5

作者：Erdogan Taskesen

在机器学任务中，确定变量间的因果关系（causality）可能是一个具有挑战性的步骤，但它对于建模工作非常重要。本文将总结有关贝叶斯概率（Bayesian probabilistic）因果模型（causal models）的概念，然后提供一个Python实践教程，演示如何使用贝叶斯结构学习来检测因果关系。

1. 背景

在许多领域，如预测、推荐系统、自然语言处理等，使用机器学习技术已成为获取有用观察和进行预测的标准工具。

虽然机器学习技术可以实现良好的性能，但提取与目标变量的因果关系并不直观。换句话说，就是：哪些变量对目标变量有直接的因果影响？

机器学习的一个分支是贝叶斯概率图模型(Bayesian probabilistic graphical models)，也称为贝叶斯网络（Bayesian networks, BN），可用于确定这些因果因素。

在我们深入讨论因果模型的技术细节之前，让我们先复习一些术语：包括"相关性"(correlation)和"关联性"(association)。

注意，相关性或关联性并不等同于因果关系。换句话说，两个变量之间的观察到的关系并不一定意味着一个导致了另一个。

从技术上讲，相关性指的是两个变量之间的线性关系，而关联性则指的是两个（或更多）变量之间的任何关系。而因果关系则意味着一个变量（通常称为预测变量或自变量）导致另一个变量（通常称为结果变量或因变量）

接下来，我将通过示例简要描述相关性和关联性。

1.1. 相关性

皮尔逊相关系数(Pearson correlation coefficient)是最常用的相关系数。系数强度由r表示，取值区间-1到1。

在使用相关性时，有三种可能的结果：

正相关：两个变量之间存在一种关系，即两个变量同时朝同一方向移动。
负相关：两个变量之间存在一种关系，即一个变量增加与另一个变量减少相关联。
无相关性：当两个变量之间没有关系时。

正相关的一个示例如图 1 所示，图中展示了巧克力消费与每个国家的诺贝尔奖获得者数量之间的关系。

图1：巧克力消费与诺贝尔奖获得者之间的相互关系

巧克力消费可能意味着诺贝尔奖获得者增加。或者反过来，诺贝尔奖获得者的增加同样可能导致巧克力消费增加。尽管存在强烈的相关性，但更有可能的是未观察到的变量，如社会经济地位或教育系统质量，可能导致巧克力消费和诺贝尔奖获得者数量的增加。

换句话说，我们仍然不知道这种关系是否是因果关系。但这并不意味着相关性本身没有用处，它只是有着不同的目的。

相关性本身并不意味着因果关系，因为统计关系并不能唯一限制因果关系。

1.1.2. 关联性

当我们谈论关联性时，我们指的是一个变量的某些值倾向于与另一个变量的某些值共同出现。

从统计学的角度来看，有许多关联性测量方法，例如卡方检验(chi-square test)、费舍尔精确检验(Fisher exact test)、超几何检验(hypergeometric test)等。它们通常用于其中一个或两个变量为有序(ordinal)或名义(nominal)变量的情况。

注意：相关性是一个技术术语，而关联性不是，因此在统计学中对其含义并不总是一致的。这意味着在使用这些术语时，明确说明其含义总是一个好的做法。

为了举例说明，我将使用超几何检验来演示是否存在两个变量之间的关联性，使用泰坦尼克号数据集。

泰坦尼克号数据集在许多机器学习示例中都有使用，众所周知，性别（女性）是生存的一个很好的预测因子。让我演示一下如何计算幸存和女性之间的关联性。

首先，安装 bnlearn 库，并仅加载泰坦尼克号数据集。

问：女性幸存的概率是多少？

零假设：幸存与性别之间没有关系。

超几何检验使用超几何分布来测量离散概率分布的统计显著性。在这个例子中， N 是总体大小（891）， K 是总体中成功状态的数量（342）， n 是样本大小/抽样次数（314）， x是样本中成功的数量（233）。

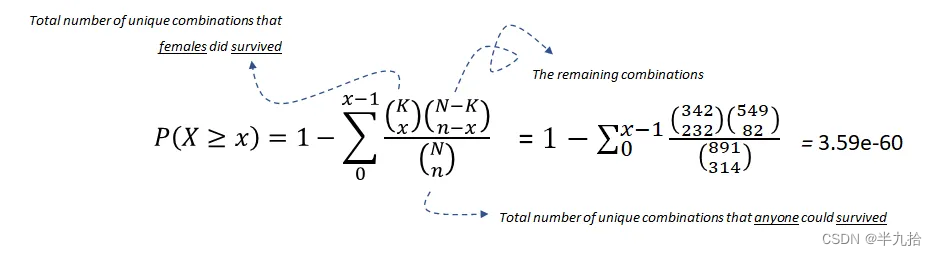
方程 1：使用超几何检验测试幸存与女性之间的关联性

在 α = 0.05 的显著性水平下，我们可以拒绝零假设，因此可以说幸存和女性之间存在统计显著的关联。

注意，关联性本身并不意味着因果关系。我们需要区分边际关联(marginal)和条件关联(conditional)。后者是因果推断的关键构建模块。

2. 因果关系

什么是因果关系（causality）？

因果关系意味着一个independent变量导致另一个dependent变量，并由 Reichenbach（1956）如下所述：

如果两个随机变量 X 和 Y 在统计上相关（ X/Y ），那么要么（a） X 导致 Y ，（b） Y 导致 X ，或者（c）存在一个第三个变量 Z 同时导致 X 和 Y 。此外，给定 Z 的条件下， X 和 Y 变得独立，即 $X\perp Y | Z$ 。

这个定义被纳入贝叶斯图模型中。

贝叶斯图模型又称贝叶斯网络、贝叶斯信念网络、Bayes Net、因果概率网络和影响图。都是同一技术，不同的叫法。

为了确定因果关系，我们可以使用贝叶斯网络（BN）。

让我们从图形开始，并可视化 Reichenbach 所描述的三个变量之间的统计依赖关系（参见图 2）。节点对应变量，有向边（箭头）表示依赖关系或条件分布。

图 2：有向无环图（DAG）编码条件独立性。（a、b、c）是等价类。（a、b）级联，（c）共同父节点，（d）是具有 V 结构的特殊类别

可以创建四个图：（a、b）级联，（c）共同父节点和（d）V 结构，这些图构成了贝叶斯网络的基础。

但是我们如何确定什么是造成什么的原因？(how can we tell what causes what?)

确定因果关系的概念思想是通过将一个节点保持不变，然后观察其影响来确定因果关系的方向，即哪个节点影响哪个节点。

举个例子，让我们看一下图 2 中的有向无环图 DAG（a），它描述了 Z 由 X引起， Y由 Z 引起。如果我们现在将 Z 保持不变，如果这个模型是正确的， Y 不应该发生变化。每个贝叶斯网络都可以用这四个图来描述，并且通过概率论（参见下面的部分），我们可以将这些部分组合起来。

需要注意的是，贝叶斯网络是有向无环图（Directed Acyclic Graph, DAG），而 DAG 是具有因果性的。这意味着图中的边是有向的，并且没有（反馈）循环（无环）。

2.1. 概率论

概率论，或者更具体地说贝叶斯定理或贝叶斯规则，构成了贝叶斯网络的基础。

贝叶斯规则用于更新模型信息，数学上表示如下方程式：

方程式由四个部分组成:

后验概率(posterior probability)是给定 X 发生的概率。
条件概率(conditional probability)或似然是在假设成立的情况下，证据发生的概率。这可以从数据中推导出来。
我们的先验(prior)信念是在观察到证据之前，假设的概率。这也可以从数据或领域知识中推导出来。
最后，边际(marginal)概率描述了在所有可能的假设下新证据发生的概率，需要计算。如果您想了解更多关于（分解的）概率分布或贝叶斯网络的联合分布的详细信息，请阅读这篇博客[6]。

3. 贝叶斯结构学习用于估计 DAG

通过结构学习，我们希望确定最能捕捉数据集中变量之间因果依赖关系的图结构。

换句话说：什么样的 DAG 最适合数据？

一种朴素的方法是简单地创建所有可能的图结构组合，即创建成十个、几百个甚至几千个不同的 DAG，直到所有组合都耗尽为止。

然后，可以根据数据的适应度对每个 DAG 进行评分。

最后，返回得分最高的 DAG。

在仅有变量X的情况下，可以创建如图 2 所示的图形以及更多的图形，因为不仅可以是 X>Z>Y（图 2a），还可以是 Z>X>Y 等等。变量X可以是布尔值（True 或 False），也可以有多个状态。

DAG 的搜索空间在最大化得分的变量数量上呈指数增长。这意味着在大量节点的情况下，穷举搜索是不可行的，因此已经提出了各种贪婪策略来浏览 DAG 空间。

通过基于优化的搜索方法，可以浏览更大的 DAG 空间。这种方法需要一个评分函数和一个搜索策略。

常见的评分函数是给定训练数据的结构的后验概率，例如BIC或BDeu。

BIC是贝叶斯信息准则（Bayesian Information Criterion）的缩写。它是一种用于模型选择的统计量，可以用于比较不同模型的拟合能力。BIC值越小，表示模型越好。在贝叶斯网络中，BIC是一种常用的评分函数之一，用于评估贝叶斯网络与数据的拟合程度。

BDeu是贝叶斯-狄利克雷等价一致先验（Bayesian-Dirichlet equivalent uniform prior）的缩写。它是一种常用的评分函数之一，用于评估贝叶斯网络与数据的拟合程度。BDeu评分函数基于贝叶斯-狄利克雷等价一致先验，该先验假设每个变量的每个可能状态都是等可能的。

在我们开始示例之前，了解何时使用哪种技术总是很好的。在搜索整个 DAG 空间并找到最适合数据的图形的过程中，有两种广泛的方法。

基于评分的结构学习
基于约束的结构学习

3.1. 基于评分的结构学习

基于评分的方法有两个主要组成部分：

搜索算法用于优化所有可能的 DAG 搜索空间；例如 ExhaustiveSearch、Hillclimbsearch、Chow-Liu 等。
评分函数指示贝叶斯网络与数据的匹配程度。常用的评分函数是贝叶斯狄利克雷分数，如 BDeu 或 K2，以及贝叶斯信息准则（BIC，也称为 MDL）。

下面描述了四种常见的基于评分的方法：

ExhaustiveSearch，顾名思义，对每个可能的 DAG 进行评分并返回得分最高的 DAG。这种搜索方法仅适用于非常小的网络，并且阻止高效的局部优化算法始终找到最佳结构。因此，通常无法找到理想的结构。然而，如果只涉及少数节点（即少于 5 个左右），启发式搜索策略通常会产生良好的结果。
Hillclimbsearch 是一种启发式搜索方法，可用于使用更多节点的情况。HillClimbSearch 实施了一种贪婪的局部搜索，从 DAG“start”（默认为断开的 DAG）开始，通过迭代执行最大化增加评分的单边操作。搜索在找到局部最大值后终止。
Chow-Liu 算法是一种特定类型的基于树的方法。Chow-Liu 算法找到最大似然树结构，其中每个节点最多只有一个父节点。通过限制为树结构，可以限制复杂性。
Tree-augmented Naive Bayes（TAN）算法也是一种基于树的方法，可用于建模涉及许多不确定性的庞大数据集的各种相互依赖特征集。

3.2. 基于约束的结构学习

一种不同但相当直观的构建 DAG 的方法是使用假设检验（如卡方检验统计量）来识别数据集中的独立性。

这种方法依赖于统计检验和条件假设，以学习模型中变量之间的独立性。

卡方检验的值是观察到的计算卡方统计量的概率，假设空设为和在给定的条件下是独立的。这可以用于在给定显著性水平的情况下进行独立判断。

约束性方法的一个示例是 PC 算法，它从一个完全连接的图开始，并根据测试的结果删除边，如果节点是独立的，直到达到停止准则。

4. 实践：基于bnlearn 库

下面介绍Python中的学习贝叶斯网络图形结构的库——bnlearn。

bnlearn能解决一些挑战，如：

结构学习：给定数据：估计捕捉变量之间依赖关系的 DAG。
参数学习：给定数据和 DAG：估计各个变量的（条件）概率分布。
推断：给定学习的模型：确定查询的精确概率值。

bnlearn 相对于其他贝叶斯分析实现有如下优势：

基于 pgmpy 库构建
包含最常用的贝叶斯管道
简单直观
开源
详细文档

4.1. 在洒水器数据集中进行结构学习

让我们从一个简单而直观的示例开始，以演示结构学习的工作原理。

假设你在后院安装了一个洒水系统，并且在过去的 1000 天里，你测量了四个变量，每个变量有两个状态：雨（是或否），多云（是或否），洒水系统（开启或关闭）和湿草（是或否）。

下面，导入 bnlearn 库，加载洒水器数据集，并确定哪个 DAG 最适合该数据。

使用 bnlearn 库，用几行代码就能确定因果关系。

请注意，洒水器数据集已经过处理，没有缺失值，所有值都处于 1 或 0 的状态。

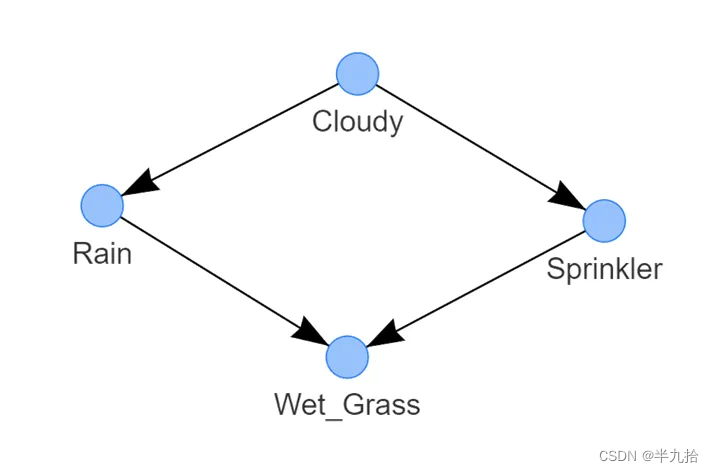
图 3：洒水器系统的最佳 DAG 示例。它表示以下逻辑：草地潮湿的概率取决于洒水器和雨水。洒水器打开的概率取决于多云的状态。下雨的概率取决于多云的状态

这样，我们有了如图 3 所示的学习到的结构。检测到的 DAG 由四个通过边连接的节点组成，每条边表示一种因果关系。

湿草的状态取决于两个节点，即雨水和洒水器；
雨水的状态由多云的状态决定；
而洒水器的状态也由多云的状态决定。

这个 DAG 表示了（因式分解的）概率分布，其中 S 是洒水器的随机变量，R 是雨水的随机变量，G 是湿草的随机变量，C 是多云的随机变量。

通过检查图形，很快就会发现模型中唯一的独立变量是 C。其他变量都取决于多云、下雨和/或洒水器的概率。

一般来说，贝叶斯网络的联合分布是每个节点在给定其父节点的条件下的条件概率的乘积:

bnlearn 在结构学习方面的默认设置是使用hillclimbsearch方法和BIC评分。

值得注意的是，可以指定不同的方法和评分类型。请参考下面的示例以指定搜索和评分类型：

# 'hc' or 'hillclimbsearch'
model_hc_bic  = bn.structure_learning.fit(df, methodtype='hc', scoretype='bic')
model_hc_k2   = bn.structure_learning.fit(df, methodtype='hc', scoretype='k2')
model_hc_bdeu = bn.structure_learning.fit(df, methodtype='hc', scoretype='bdeu')

# 'ex' or 'exhaustivesearch'
model_ex_bic  = bn.structure_learning.fit(df, methodtype='ex', scoretype='bic')
model_ex_k2   = bn.structure_learning.fit(df, methodtype='ex', scoretype='k2')
model_ex_bdeu = bn.structure_learning.fit(df, methodtype='ex', scoretype='bdeu')

# 'cs' or 'constraintsearch'
model_cs_k2   = bn.structure_learning.fit(df, methodtype='cs', scoretype='k2')
model_cs_bdeu = bn.structure_learning.fit(df, methodtype='cs', scoretype='bdeu')
model_cs_bic  = bn.structure_learning.fit(df, methodtype='cs', scoretype='bic')

# 'cl' or 'chow-liu' (requires setting root_node parameter)
model_cl      = bn.structure_learning.fit(df, methodtype='cl', root_node='Wet_Grass')

尽管洒水器数据集的检测到的 DAG 具有启示性，并显示了数据集中变量的因果依赖关系，但它并不能让你提出各种问题，例如：

如果洒水器关闭，草地湿润的概率有多大？
如果洒水器关闭且多云，下雨的概率有多大？

在洒水器数据集中，根据你对世界的了解和逻辑思考，结果可能是显而易见的。但是，一旦你拥有更大、更复杂的图形，可能就不再那么明显了。

通过所谓的推断，我们可以回答“如果我们做了 X 会怎样”类型的问题，这些问题通常需要进行控制实验和明确的干预才能回答。

4.2. 如何进行推断？

要进行推断，我们需要两个要素：DAG 和条件概率表（Conditional Probabilistic Tables, CPTs）。

此时，我们已经将数据存储在数据框（df）中，并且已经计算出描述数据结构的 DAG。需要使用参数学习计算 CPTs，以定量地描述每个节点与其父节点之间的统计关系。

让我们首先进行参数学习，然后再回到推断的过程中。

4.2.1. 参数学习

参数学习是估计条件概率表（CPTs）的值的任务。

bnlearn 库支持离散和连续节点的参数学习：

最大似然估计是使用变量状态出现的相对频率进行的自然估计。在对贝叶斯网络进行参数估计时，数据不足是一个常见问题，最大似然估计器存在对数据过拟合的问题。换句话说，如果观察到的数据对于基础分布来说不具有代表性（或者太少），最大似然估计可能会相差甚远。例如，如果一个变量有 3 个可以取 10 个状态的父节点，那么状态计数将分别针对 $10^3 = 1000$ 个父节点配置进行。这使得最大似然估计对学习贝叶斯网络参数非常脆弱。减轻最大似然估计过拟合的一种方法是贝叶斯参数估计。
贝叶斯估计从已存在的先验 CPTs 开始，这些 CPTs 表示在观察到数据之前我们对变量的信念。然后，使用观察数据的状态计数来更新这些“先验”。可以将先验视为伪状态计数，在归一化之前将其添加到实际计数中。一个非常简单的先验是所谓的 K2 先验，它只是将“1”添加到每个单独状态的计数中。一个更明智的先验选择是 BDeu（贝叶斯狄利克雷等效均匀先验）。

我继续使用洒水器数据集来学习其参数，并检测条件概率表（CPTs）。

要学习参数，我们需要一个有向无环图（DAG）和一个具有完全相同变量的数据集,思路是将数据集与 DAG 连接起来。在之前的示例中，我们已经计算出了 DAG（图 3）。

如果你已经到达这一点，您已经使用最大似然估计（MLE）基于 DAG 和输入数据集 df 计算了 CPTs（图 4）。请注意，为了清晰起见，CPTs 在图 4 中包含在内。

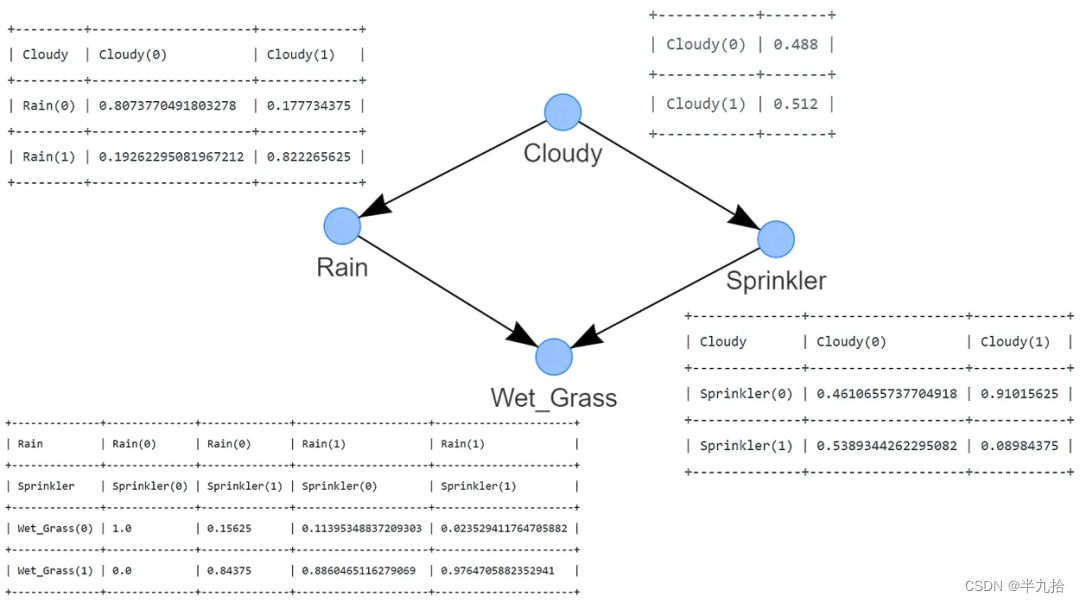
图 4：使用最大似然估计进行参数学习推导的 CPTs

使用 MLE 计算 CPTs 非常简单，让我通过示例来演示一下，手动计算节点 Cloudy 和 Rain 的 CPTs。

# Examples to illustrate how to manually compute MLE for the node Cloudy and Rain:# Compute CPT for the Cloudy Node:# This node has no conditional dependencies and can easily be computed as following:# P(Cloudy=0)sum(df['Cloudy']==0) / df.shape[0] # 0.488# P(Cloudy=1)sum(df['Cloudy']==1) / df.shape[0] # 0.512# Compute CPT for the Rain Node:# This node has a conditional dependency from Cloudy and can be computed as following:# P(Rain=0 | Cloudy=0)sum( (df['Cloudy']==0) & (df['Rain']==0) ) / sum(df['Cloudy']==0) # 394/488 = 0.807377049# P(Rain=1 | Cloudy=0)sum( (df['Cloudy']==0) & (df['Rain']==1) ) / sum(df['Cloudy']==0) # 94/488  = 0.192622950# P(Rain=0 | Cloudy=1)sum( (df['Cloudy']==1) & (df['Rain']==0) ) / sum(df['Cloudy']==1) # 91/512  = 0.177734375# P(Rain=1 | Cloudy=1)sum( (df['Cloudy']==1) & (df['Rain']==1) ) / sum(df['Cloudy']==1) # 421/512 = 0.822265625

请注意，条件依赖关系可能基于有限的数据点。例如， $p(rain=1|cloudy=0)$ 基于 91 个观测结果。如果 Rain 有更多的状态和/或更多的依赖关系，这个数字可能会更低。更多的数据是否是解决方案？也许是，也许不是。只要记住，即使总样本量非常大，由于状态计数是针对每个父节点的配置进行条件计数，这也可能导致分段。与 MLE 方法相比，查看 CPT 与之间的差异。

4.2.2. 在 Sprinkler 数据集上进行推理

进行推理需要贝叶斯网络具备两个主要组成部分：描述数据结构的有向无环图（DAG）和描述每个节点与其父节点之间的统计关系的条件概率表（CPT）。到目前为止，您已经拥有数据集，使用结构学习计算了 DAG，并使用参数学习估计了 CPT。现在可以进行推理了！

在推理中，我们使用一种称为变量消除的过程来边缘化变量。变量消除是一种精确的推理算法。通过简单地将求和替换为最大函数，它还可以用于确定具有最大概率的网络状态。不足之处是，对于大型的贝叶斯网络，它可能在计算上是棘手的。在这些情况下，可以使用基于采样的近似推理算法，如 Gibbs 采样或拒绝采样 [7]。

使用 bnlearn，我们可以进行如下的推理：

import bnlearn as bn

# Load sprinkler dataset
df = bn.import_example('sprinkler')

# Define the causal dependencies based on your expert/domain knowledge.
# Left is the source, and right is the target node.
edges = [('Cloudy', 'Sprinkler'),
         ('Cloudy', 'Rain'),
         ('Sprinkler', 'Wet_Grass'),
         ('Rain', 'Wet_Grass')]


# Create the DAG
DAG = bn.make_DAG(edges)

# Parameter learning on the user-defined DAG and input data using Bayes to estimate the CPTs
model = bn.parameter_learning.fit(DAG, df, methodtype='bayes')
bn.print_CPD(model)

q1 = bn.inference.fit(model, variables=['Wet_Grass'], evidence={'Sprinkler':0})
print(q1.df)
# +--------------+------------------+
# | Wet_Grass    |   phi(Wet_Grass) |
# +==============+==================+
# | Wet_Grass(0) |           0.4869 |
# +--------------+------------------+
# | Wet_Grass(1) |           0.5131 |
# +--------------+------------------+


q2 = bn.inference.fit(model, variables=['Rain'], evidence={'Sprinkler':0, 'Cloudy':1})
print(q2.df)
# +---------+-------------+
# | Rain    |   phi(Rain) |
# +=========+=============+
# | Rain(0) |      0.3370 |
# +---------+-------------+
# | Rain(1) |      0.6630 |
# +---------+-------------+

# Inferences with two or more variables can also be made such as:
q3 = bn.inference.fit(model, variables=['Wet_Grass','Rain'], evidence={'Sprinkler':1})
print(q3.df)
# +--------------+---------+-----------------------+
# | Wet_Grass    | Rain    |   phi(Wet_Grass,Rain) |
# +==============+=========+=======================+
# | Wet_Grass(0) | Rain(0) |                0.1811 |
# +--------------+---------+-----------------------+
# | Wet_Grass(0) | Rain(1) |                0.1757 |
# +--------------+---------+-----------------------+
# | Wet_Grass(1) | Rain(0) |                0.3555 |
# +--------------+---------+-----------------------+
# | Wet_Grass(1) | Rain(1) |                0.2877 |
# +--------------+---------+-----------------------+

现在我们已经得到了我们的问题的答案：

如果喷灌系统关闭，草坪潮湿的可能性有多大？P(Wet_grass=1 | Sprinkler=0) = 0.51

如果喷灌系统关闭并且天阴，有下雨的可能性有多大？P(Rain=1 | Sprinkler=0, Cloudy=1) = 0.663

4.3. 我如何知道我的因果模型是正确的？

如果仅使用数据来计算因果图，很难完全验证因果图的有效性和完整性。然而，有一些解决方案可以帮助增加对因果图的信任。例如，可以对变量集之间的某些条件独立性或依赖性关系进行经验性测试。如果它们在数据中不存在，则表明因果模型的正确性。或者，可以添加先前的专家知识，例如 DAG 或 CPT，以在进行推理时增加对模型的信任。

5. 讨论

在本文中，涉及了一些关于为什么相关性或关联不等于因果性以及如何从数据向因果模型的转变使用结构学习的概念。

贝叶斯技术的优势总结如下：

后验概率分布的结果或图形使用户能够对模型预测做出判断，而不仅仅是获得单个值作为结果。
可以将领域/专家知识纳入到 DAG 中，并在不完整信息和缺失数据的情况下进行推理。这是可能的，因为贝叶斯定理基于用证据更新先验项。
具有模块化的概念。
通过组合较简单的部分来构建复杂系统。
图论提供了直观的高度交互的变量集。
概率论提供了将这些部分组合在一起的方法。

然而，贝叶斯网络的一个弱点是寻找最佳 DAG 在计算上很耗时，因为必须对所有可能的结构进行详尽搜索。

穷举搜索的节点限制可以达到约 15 个节点，但也取决于状态的数量。如果有更多的节点，就需要使用具有评分函数和搜索算法的替代方法。尽管如此，要处理具有数百甚至数千个变量的问题，需要使用基于树或基于约束的方法，并使用变量的黑名单/白名单。这种方法首先确定顺序，然后找到该顺序的最佳 BN 结构。这意味着在可能的排序搜索空间上进行工作，这比网络结构空间小得多。

确定因果关系可能是一项具有挑战性的任务，但 bnlearn 库旨在解决其中一些挑战，如结构学习、参数学习和推理。它还可以推导出（整个）图的拓扑排序或比较两个图。

References

McLeod, S. A, Correlation definitions, examples & interpretation. Simply Psychology, 2018, January 14
F. Dablander, An Introduction to Causal Inference, Department of Psychological Methods, University of Amsterdam, https://psyarxiv.com/b3fkw
Brittany Davis, When Correlation is Better than Causation, Medium, 2021
Paul Gingrich, Measures of association. Page 766–795
Taskesen, E, Explore and understand your data with a network of significant associations. Aug. 2021, Medium
Branislav Holländer, Introduction to Probabilistic Graphical Models, Medium, 2020
Harini Padmanaban, Comparative Analysis of Naive Analysis of Naive Bayes and Tes and Tree Augmented Naive augmented Naive Bayes Models, San Jose State University, 2014
Huszar. F, ML beyond Curve Fitting: An Intro to Causal Inference and do-Calculus
E. Perrier et al, Finding Optimal Bayesian Network Given a Super-Structure, Journal of Machine Learning Research 9 (2008) 2251–2286.