一、说明
这是卡尔曼滤波器系列的第二部分,我们在概念和代码方面对卡尔曼滤波器进行了基于示例的理解。在第一部分中,我们对卡尔曼滤波器有了直观的理解,然后是基于数值的 Alpha-Beta 滤波器(构成卡尔曼滤波器的基础)的正式示例。
在本文中,我们正式介绍贝叶斯滤波器和卡尔曼滤波器。在我们在下一篇文章中正式介绍卡尔曼滤波器之前,这篇文章将介绍贝叶斯滤波器。
但您可能会问,为什么要使用贝叶斯过滤器呢?稍安毋躁!我们很快就会做到这一点 🙂
如果您还没有阅读第一部分,本系列分为以下几个部分:
- 直观了解卡尔曼滤波器、Alpha-Beta滤波器;
- 正式贝叶斯过滤器(我们在这里!);
- 形式卡尔曼滤波器;
- Python 中的一维卡尔曼滤波器从头开始;
- Python 中的二维卡尔曼滤波器从头开始。
二、快速回顾
如果我们要总结上一篇文章第 1 部分,要点如下!
卡尔曼滤波器是一种工具,可以帮助您高精度地估计状态,即使传感器测量结果存在噪声和/或不确定。
它使用数学模型来预测时间实例t的状态值,基于状态值在前一个时间实例t-1中的位置以及它应如何在数学上演化(状态估计)。然后,它将该预测与在时间 t 接收到的传感器测量值进行比较,并根据差异调整其估计(状态更新)。
使这个稍微正式一些,卡尔曼滤波器有两个步骤:
- 状态预测:根据 t-1 时刻的估计值,预测t时刻的状态值。它使用状态传播/外推模型来预测该值;
- 状态更新:将状态预测的预测与测量值(均针对时间t)进行比较,并根据差异更新/调整其对时间t的最终估计。此步骤使用传感器/探测器。
如果这个回顾没有让你说“呃!我已经知道了”,请看第 1 部分。
我们现在要更深入地了解卡尔曼滤波器吗?不,不!还没有!为此,我们首先要看看它的父亲——贝叶斯过滤器。当然,我们还将它连接到我们之前探索过的 Alpha-Beta 过滤器。
三、贝叶斯过滤器 — 基于示例的推导

自动赛车远离天线的示例,该天线测量其在不同时间戳中的位置。
在第 1 部分中,我们介绍了需要及时定位/跟踪的自动驾驶汽车的示例。假设速度恒定,汽车沿直线行驶。对于每个时间戳t,我们根据恒定速度假设和天线测量来估计汽车的行驶距离。简单易行,对吧?
为了形式化这一点,我们在示例中将变量分配给不同的值 -
- z——传感器观测(天线测量);
- u — 控制数据(在我们的例子中为恒定速度);
- x — 系统状态(汽车距原点的距离,这里恰好是天线)。
因此,我们有传感器观测值z、控制数据u和系统状态x。这些变量对于我们的示例来说是明确定义的,但它们可能会根据问题陈述和方法而有所不同。例如,系统的状态可以是机器人在环境中的位置,或者世界上地标的位置,即我们想要估计的任何东西。如果我们能够感知环境,并可能通过执行任何操作来修改它,我们就可以对其进行估计。
注 - 在许多示例中,系统状态包括位置和速度。在这种情况下,控制数据 u 可以是加速度。如果我们遵循该模型,则 u=0(恒定速度)。但我们仍然会有相同的模型行为。如果这还没有意义,别担心!
现在是时候解释这些变量在概率世界中是如何相关的了。由于我们知道传感器观测值z和控制数据u,因此只有系统状态x未知。因此,我们问自己:“给定传感器观测值 z 和控制数据 u,系统的状态 x 是什么?” 这本质上就是我们的问题陈述,对吗?
从数学上来说,这个方程相当于
![]()
解释该方程的另一种可能的方式是:“给定 z 和 u,系统状态为 x 的可能性有多大?”。这个概率可以是均匀分布,随着我们获得更多的观察并执行操作,我们对状态更加确定。最后,我们希望得到一个围绕一个状态的峰值分布,我们也希望它是正确的。说到这里,我们永远不能说系统完全处于那个特定状态,因为我们这里有一个概率分布,而且它永远不是百分百确定的。
该方程估计了观测和控制数据后系统的状态,这就是它也称为后验方程的原因。为了估计这样的后验,我们可以将贝叶斯规则与概率论中的其他规则结合使用。最后,我们将提出一个递归方程,使我们能够一次集成一个传感器观测和一个控制,以递归地估计系统的状态。
所以我们从下面的第一个方程开始
![]()
这和前面的方程一模一样,只是我们引入了时间的概念。简而言之,它表示:“给定所有观测集 z ₁:ₜ和所有控制集 u ₁:ₜ ,我对时间实例 t, bel(xₜ) 的当前状态的信念是什么?” 。那么,考虑到现在为止的所有数据,包括时间实例t,系统的状态是什么?我们可以将贝叶斯规则应用于这个方程。但首先,让我们了解什么是贝叶斯规则。
两个不同事件a和b发生的概率为
![]()
然而, a和b的概率也等于b的概率乘以给定b的概率。因此,
![]()
如果我们继续从这两个方程出发,我们有
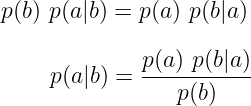
这就是贝叶斯规则。
贝叶斯规则描述了基于可能与a相关的条件b的先验知识的事件 a 的概率。为了简化,我们可以将p(b) ⁻¹ 称为贝叶斯规则中的归一化器,然后它就变成
![]()
现在我们了解了贝叶斯规则是什么,让我们回到我们的主要方程并继续定义信念。同样,我们有一系列传感器观测值和一系列运动(控制)数据,我们想要估计系统的当前状态
![]()
如果我们将贝叶斯规则应用于该方程,我们最终会得到以下新方程
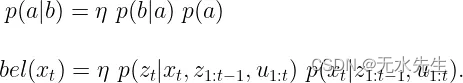
我们交换了xₜ和zₜ(相当于p(b|a)),并将传感器观测序列的其余部分z ₁:ₜ₋₁ 留在右侧。然后我们有第二项(相当于p(a)),但仍然忽略当前传感器观测值z ₜ。这就是贝叶斯规则的基本执行,没有任何棘手的动作。
现在我们可以根据马尔可夫假设简化这个新方程的第一部分。它假设如果未来状态的条件概率分布仅依赖于当前数据来估计未来状态,则过去的数据是不必要的。对于我们的情况,如果我们知道系统的状态xₜ,并且我们想要估计当前传感器观测值z ₜ ,那么可以忽略先前的观测值和运动数据(因为它们仅用于估计系统的状态)系统,目前已知)。因此,

为了处理这个新方程的第二部分,我们必须理解它的含义。我们想要根据除最后一个z ₁:ₜ₋₁ 之外的所有传感器观测值以及所有控制数据u ₁:ₜ来估计系统的当前状态xₜ 。对于这种估计,我们需要使用全概率定律。它呈现了可以通过几个不同事件计算的结果的总概率。其积分版本为
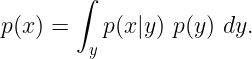
简单来说,变量x的分布等于给定y时x发生的概率乘以所有可能y的y发生的可能性。
注意 - 该积分用于连续模型。如果您的模型是离散的,则可以使用 sigma 表示法。
如果我们将此定律应用于bel(xₜ)方程的第二部分,以计算基于x ₜ₋₁的积分(它表示前一个时间步中系统的状态),我们有以下结果
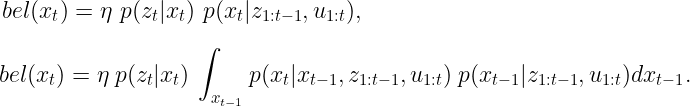
通过将马尔可夫假设应用于积分的第一项,我们可以简化整个方程。这个想法很简单——如果我们想要估计系统的当前状态xₜ,假设我们知道之前的状态xₜ₋₁ ,那么在t-1之前收集的所有传感器数据对我们来说都是不必要的。考虑到在时间t没有获取传感器观测值(由于z₁:ₜ₋₁),并且只有控制数据(由于u₁:ₜ),我们最终得到
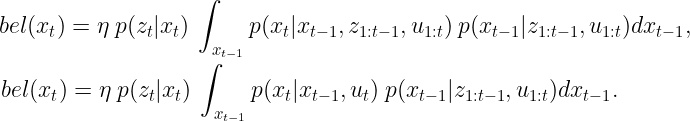
继续化简,积分的第二项也可以化简。如果我们估计时间戳t-1处的系统状态,则与当前时间t相对应的所有数据都变得不必要。这也是基于马尔可夫假设。因此,
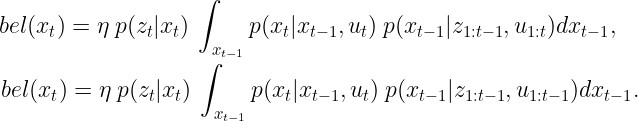
经过这么多工作,我们最终得到了一个很长的方程。但你看到这里有一个模式吗?
我们用下面的等式开始这个练习
![]()
它正是积分的第二项,除了索引(从t到t-1)。这意味着积分具有前一个时间戳中系统状态的置信度,即
![]()
因此,我们可以说
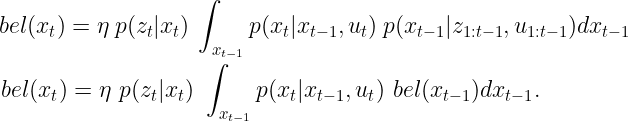
最后,我们有一个递归更新方案,允许我们根据先前的状态和控制数据(当前运动)以及当前的传感器观察来估计系统的状态。
现在我们有了递归更新方程,我们可以根据它们在整个方案中的角色来拆分它。我们将其分为两个步骤:预测和更新。看看我们如何将其与上一篇文章中的理解联系起来?
我们现在有了预测和更新步骤的数学表示,而我们只是概念性地掌握了一些东西。
我们方程的这一部分是预测步骤

它考虑了对系统先前状态的置信度和控制数据(将系统从先前状态转变为当前状态的操作),以估计预测的置信度。
基本上,它根据先前的估计和控制数据(动作)来预测状态将是什么。
这里有一个例子可以让这个方程更加直观:想象一下你在足球场中心,看着一个球门。你的位置就是你的状态,xₜ₋₁。然后你向前迈出两步,用 uₜ(控制/动作)表示。您最终所处的位置是根据前面的方程以及您对两步将引导您走向何方的内心想法来估计的。它表示为上划线{bel}(xₜ)。
等式的另一部分是我们的更新步骤
![]()
它依赖于预测信念和传感器观察来估计当前更新的信念。归一化因子有助于将积分结果和总体结果保持为 1(因为总和在概率上不能大于 1)。
回到足球场的例子——现在你回头看看,大致了解自己前进了多少。这是您的测量值zₜ,更新方程使用它来估计您的当前位置bel(xₜ)以及预测位置overline{bel}(xₜ)。
但这两个方程还有更多内容!
在预测步骤中,我们仅处理控制数据和系统的先前状态。必须对控制数据进行建模,为此,我们使用运动模型
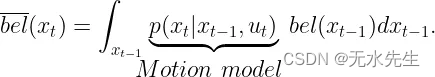
这同样适用于更新步骤,但适用于传感器观测。如果我们可以更新系统的状态,并且对传感器观测进行正确建模,我们就可以纠正预测。所以,
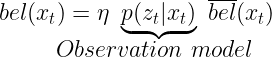
这意味着我们现在有了预测和更新步骤的数学表示。
顺便说一句,你最终在这里看到的是贝叶斯过滤器!我们用贝叶斯定理、概率论和我们的例子构建了一个贝叶斯过滤器。总是比乱扔行话要好,对吧?😃
本质上,贝叶斯过滤器可以写成一个两步过程——预测和更新。
基于贝叶斯滤波器的递归遗产估计框架的介绍到此结束。它是一个通用框架,使用运动和观察两种模型来估计状态。
注意 — 您现在是否也明白这在概念上与 Alpha-Beta 过滤器有何相似之处?您现在知道为什么我们从基本的 Alpha-Beta 过滤器开始了。您很快就会看到,与 Alpha-Beta 滤波器不同,卡尔曼滤波器如何计算运行时每次迭代的权重。但一切都来得正是时候!
四、卡尔曼滤波器与贝叶斯滤波器有何关系?
在我们深入讨论卡尔曼滤波器和贝叶斯滤波器之间的关系之前,我们先给您一些剧透。
卡尔曼滤波器是实现贝叶斯滤波器的一种方式。它是一个有 2 个假设的贝叶斯过滤器:
- 所有分布都是高斯分布;
- 状态外推(运动)模型和测量(观测)模型都是线性的(或线性化的)。
现在我们再多谈谈吧。
贝叶斯滤波器在给定先验分布和当前测量的情况下估计状态的后验概率分布。后验分布代表了我们在合并测量信息后对状态的信念。然而,在实践中,直接计算和表示完整的后验分布可能在计算上非常昂贵,甚至对于高维系统来说是不可行的。卡尔曼滤波器(贝叶斯滤波器+上面的两个假设)解决了这个问题。
卡尔曼滤波器为具有高斯噪声的线性动态系统的贝叶斯滤波器问题提供了特定的解决方案。它假设系统动力学和测量模型都是线性的,并且噪声遵循已知统计数据的高斯分布。卡尔曼滤波器使用两步过程:预测步骤和更新步骤,正如我们已经介绍的那样。通过迭代地应用预测和更新步骤,卡尔曼滤波器提供了一种有效且最优的解决方案来估计给定噪声测量的线性系统的状态。随着新测量的出现,它不断完善状态估计。
值得注意的是,贝叶斯滤波器还有其他变体,可以扩展卡尔曼滤波器处理非线性系统或非高斯噪声的能力。例如,在处理非线性系统动力学时,通常使用扩展卡尔曼滤波器(EKF)和无迹卡尔曼滤波器(UKF)。这些滤波器采用近似值通过非线性模型传播概率分布,并根据测量结果更新状态估计。
五、总结
到目前为止,我们已经深入研究了状态估计的迷人世界,并探索了贝叶斯滤波器的强大技术,它构成了卡尔曼滤波器的基础。让我们回顾一下本系列到目前为止所涵盖的内容:
- 在上一篇文章中,我们讨论了在存在噪声和不确定性的情况下估计系统状态的挑战。通过移动汽车的例子,我们引入了状态估计的概念。我们谈到了结合测量和先验知识来完善我们对系统真实状态的理解的重要性。我们还引入了 alpha-beta 滤波器,以了解预测和更新步骤如何帮助离散状态估计;
- 在这篇文章中,我们重点关注贝叶斯过滤器,这是一种利用贝叶斯推理的递归状态估计的通用框架。我们了解到,贝叶斯滤波器的目的是在给定先验分布和当前测量的情况下计算系统状态的后验概率分布。随着时间的推移,我们可以根据新信息更新我们对国家的信念,从而获得越来越准确的估计;
- 为了更好地掌握贝叶斯滤波器的数学基础,我们研究了它的关键方程。我们探索了先验分布、动态模型和测量模型如何结合起来计算后验分布。理解这些方程有助于我们理解状态估计的概率本质以及如何迭代地改进它;
- 我们还发现了贝叶斯滤波器和卡尔曼滤波器之间的密切关系。卡尔曼滤波器是贝叶斯滤波器的具体实现,专为具有高斯噪声的线性动态系统而定制。虽然贝叶斯滤波器提供了一个通用框架,但卡尔曼滤波器的线性和高斯噪声假设允许更有效和最佳的状态估计。
现在我们对贝叶斯滤波器有了很好的了解,我们在下一部分中继续讨论卡尔曼滤波器。