Leetcode—4.寻找两个正序数组的中位数【困难】

news2024/10/5 17:22:00

2023每日刷题（二十九）

Leetcode—4.寻找两个正序数组的中位数

在这里插入图片描述

直接法实现代码

int mid, mid1, mid2;
bool findmid(int n, int k, int x) {
    if(n % 2 == 1) {
        if(k == n / 2) {
            mid = x;
            return true;
        }
    } else {
        if(k == n / 2 - 1) {
            mid1 = x;
        } else if(k == n / 2) {
            mid2 = x;
            return true;
        }
    }
    return false;
}

double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
    int n = nums1Size + nums2Size;
    int i = 0, j = 0, k = 0;
    bool flag = false;
    while(i < nums1Size && j < nums2Size) {
        if(nums1[i] < nums2[j]) {
            flag = findmid(n, k, nums1[i]);
            if(flag) {
                break;
            }
            i++;
        } else {
            flag = findmid(n, k, nums2[j]);
            if(flag) {
                break;
            }
            j++;
        }
        k++;
    }
    while(i < nums1Size && !flag) {
        flag = findmid(n, k, nums1[i]);
        k++;
        i++;
    }
    while(j < nums2Size && !flag) {
        flag = findmid(n, k, nums2[j]);
        k++;
        j++;
    }
    if(n % 2 == 1) {
        return mid;
    } else {
        return (mid1 + mid2) / 2.0;
    }
}

运行结果

在这里插入图片描述

优化代码

double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
    int n = nums1Size + nums2Size;
    int mid1 = 0, mid2 = 0;
    int i = 0, j = 0, k = 0;
    while((i < nums1Size || j < nums2Size) && k <= n / 2) {
        if((j >= nums2Size) || (i < nums1Size && nums1[i] <= nums2[j])) {
            if(k == n / 2) {
                mid1 = nums1[i];
            } else if(k == n / 2 - 1) {
                mid2 = nums1[i];
            }
            i++;
        }
        else {
            if(k == n / 2) {
                mid1 = nums2[j];
            } else if(k == n / 2 - 1) {
                mid2 = nums2[j];
            }
            j++;
        }
        k++;
    }
    if(n % 2 == 1) {
        return mid1;
    } else {
        return (mid1 + mid2) / 2.0;
    }
}

运行结果

在这里插入图片描述

二分法算法思想——降低时间复杂度到题目要求的 $O (l o g (m + n))$

其实就是第 k 小数解法，详情参考这篇文章
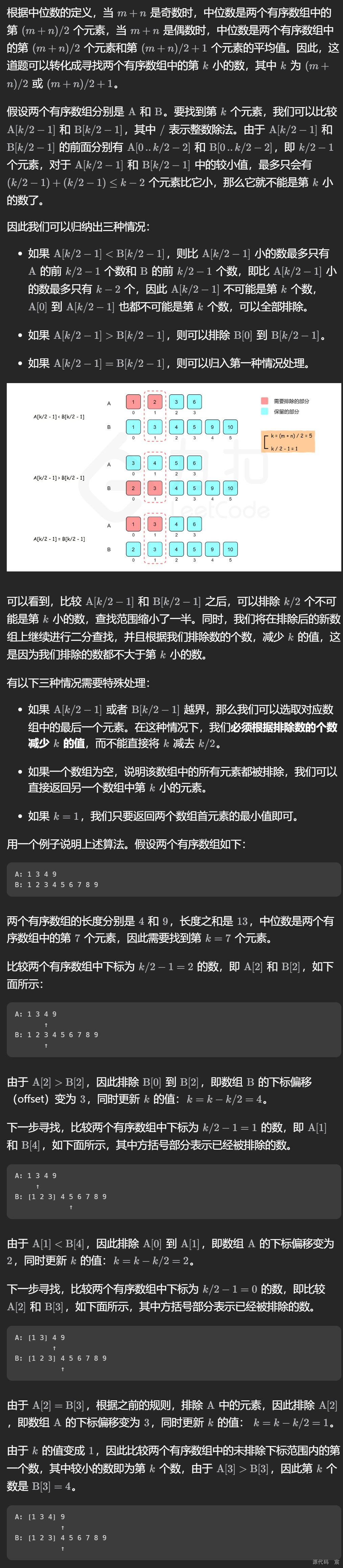
在这里插入图片描述

二分法实现代码

#define MIN(a, b) ((a < b) ? (a): (b))
int binaryKth(int* nums1, int nums1Size, int* nums2, int nums2Size, int k) {
    int idx1 = 0, idx2 = 0;
    int newIdx1 = 0, newIdx2 = 0;
    int n1 = 0, n2 = 0;
    while(1) {
        if(idx1 == nums1Size) {
            return nums2[idx2 + k - 1];
        }
        if(idx2 == nums2Size) {
            return nums1[idx1 + k - 1];
        }
        if(k == 1) {
            return MIN(nums1[idx1], nums2[idx2]);
        }
        newIdx1 = MIN(idx1 + k / 2 - 1, nums1Size - 1);
        newIdx2 = MIN(idx2 + k / 2 - 1, nums2Size - 1);
        n1 = nums1[newIdx1];
        n2 = nums2[newIdx2];
        if(n1 <= n2) {
            k -= newIdx1 - idx1 + 1;
            idx1 = newIdx1 + 1;
        } else {
            k -= newIdx2 - idx2 + 1;
            idx2 = newIdx2 + 1;
        }
    }
}

double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
    int n = nums1Size + nums2Size;
    if(n % 2 == 1) {
        return binaryKth(nums1, nums1Size, nums2, nums2Size, (n + 1) / 2);
    } else {
        int a = binaryKth(nums1, nums1Size, nums2, nums2Size, n / 2);
        int b = binaryKth(nums1, nums1Size, nums2, nums2Size, n / 2 + 1);
        return (a + b) / 2.0;
    }
}