一、介绍
红黑树也是对一般的搜索二叉树不能保证平衡的一个改进,和AVL树采用的思路不同,但同样需要旋转,其本质也是一颗平衡搜索二叉树,其节点有颜色的区分,并且被一些规则束缚,在这些规则下,能够使得树最长路径的长度不会高于最短路径的两倍
二、红黑树的性质
1.红黑树的节点,不是红色,就是黑色
2.根节点是黑色的
3.路径上不能出现两个连续的红色节点
4.每条路径上的黑色节点数量相同
5.每个叶子节点指向的空节点,默认认为是黑色的
遵循以上规则,则可以保证最长的路径的长度不会超过最短路径的两倍,因此红黑树实现平衡的核心,就是对新插入的节点使其通过一系列操作,满足上面的五个条件即可
三、红黑树的定义
插入的节点默认为红色,是为了能够调整,插入红色,可能只需要局部调整,若是黑色,则每次插入都必然会影响所有路径

四、红黑树的核心实现Insert
1.基本框架
先是插入数据,然后再是根据规则做出调整,红黑树实现的核心就在于如何调整,使得各种情况的插入都可以调整成符合规则的样子
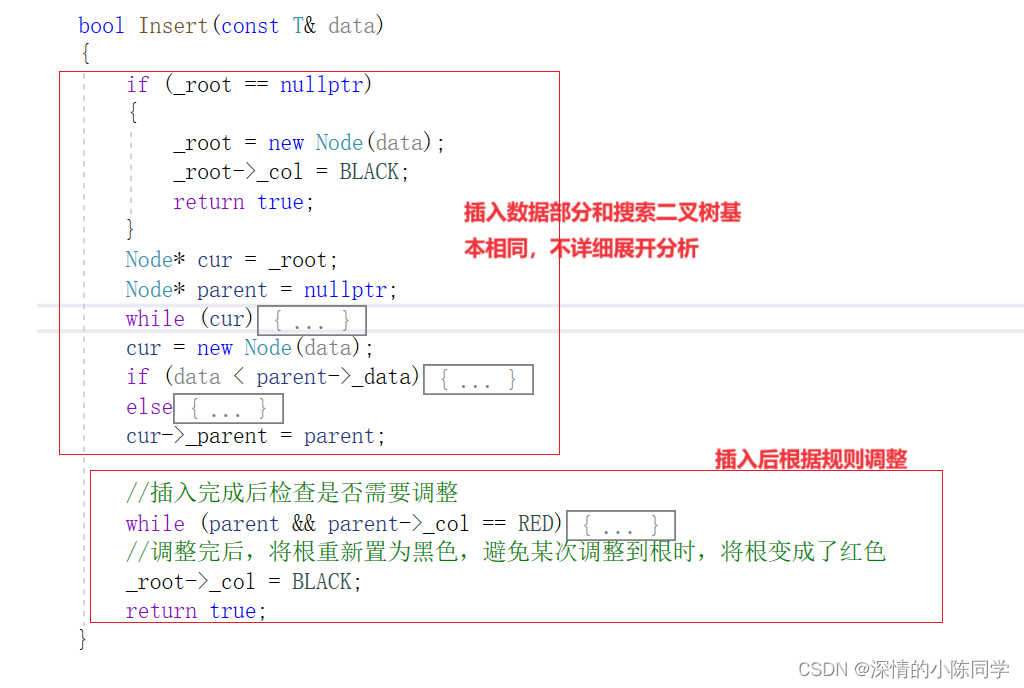
2.调整分析

情况一:当插入一个新的节点cur为根节点,则直接插入,并且将颜色改为黑色即可
(根节点为黑色)
情况二:继续插入,若是parent节点为黑色,则插入一个红色节点不会破坏规则,因此无需调整
(不能有连续的红色节点,每个路径黑色节点相同)
情况三:插入cur节点,其parent节点也是红色,则出现了两个连续的红色节点,需要根据不同情况进行分类调整:
(1).uncle存在且为红
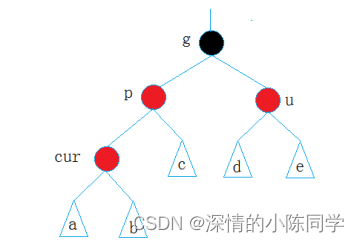
处理:将parent和uncle变黑,将grandfather变红,然后继续向上调整,cur指向g
parent指向g->_parent
p和u同时变黑,使得g左右两边路径同时增加了一个黑色节点,因此需要将g变红,这样既不影响黑色节点的规则,也没有连续出现的红色节点,但是由于g变红,因此可能会对上面部分造成影响,所以需要继续向上调整,将cur指向grandfather,parent指向g的parent往上继续检查
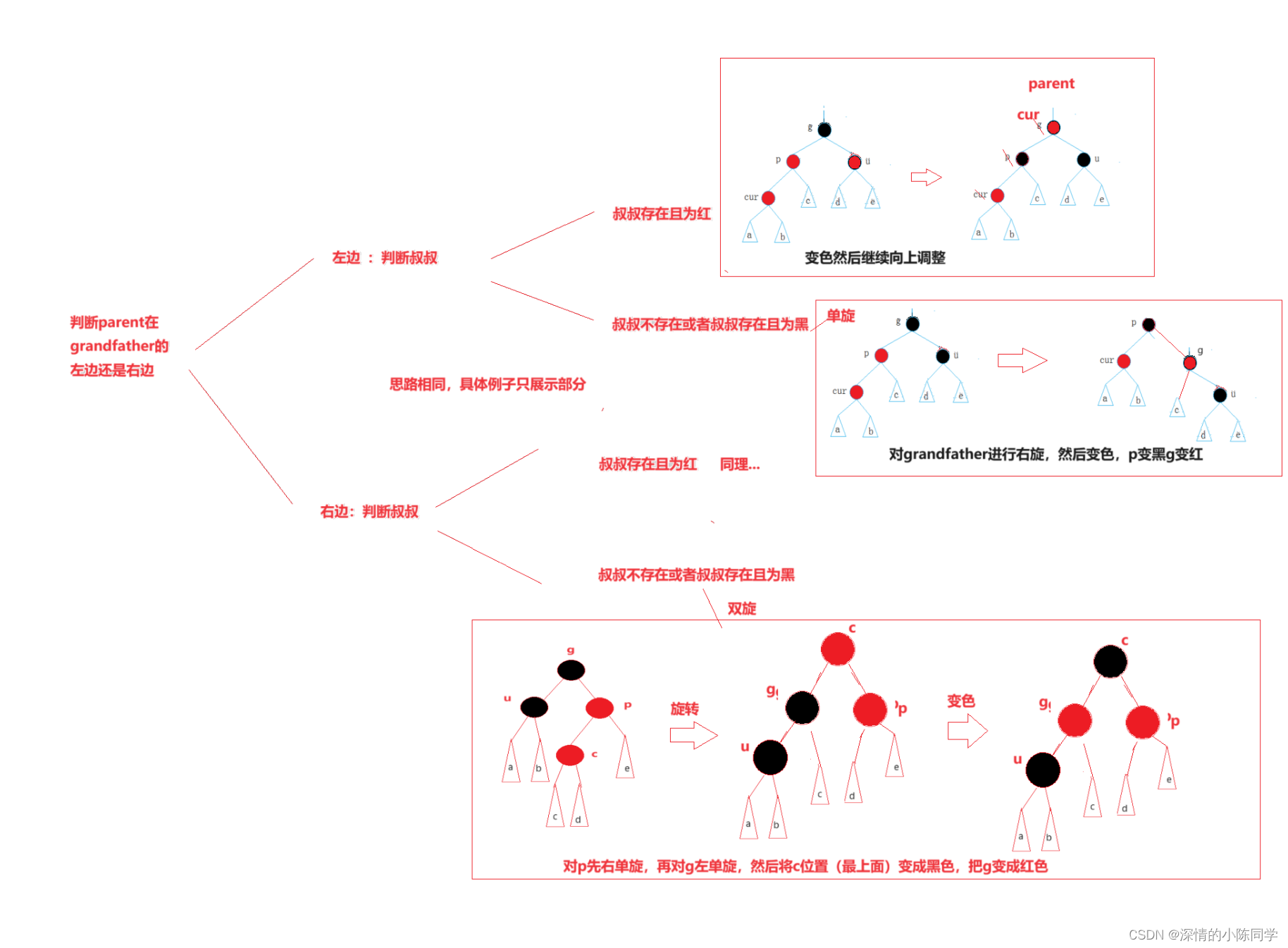
(2)uncle不存在或者存在且为黑

处理:根据具体情况进行旋转(单旋、双旋),旋转后再将局部最上方的变黑,grandfather变红
旋转即降了高度,并且旋转后通过调整颜色,使得局部内同时符合黑色和红色的约束条件
需要特殊处理的就只有这两种情况,但在代码实现的角度,需要对这两种情况进行细分,首先是先判断parent在grandfather的左边还是右边,这个影响着旋转往哪边旋,然后再是分“叔叔存在且为红”和“叔叔不在或者在且为黑”这两种情况分类讨论,但是处理的思路是一样的,只是在细节上要根据具体情况进行调整,在“叔叔不在或者在且为黑”的条件下,需要继续细分cur在parent的左边还是右边,确定具体是单旋还是双旋,旋转后再变色即可
3.代码实现部分分析
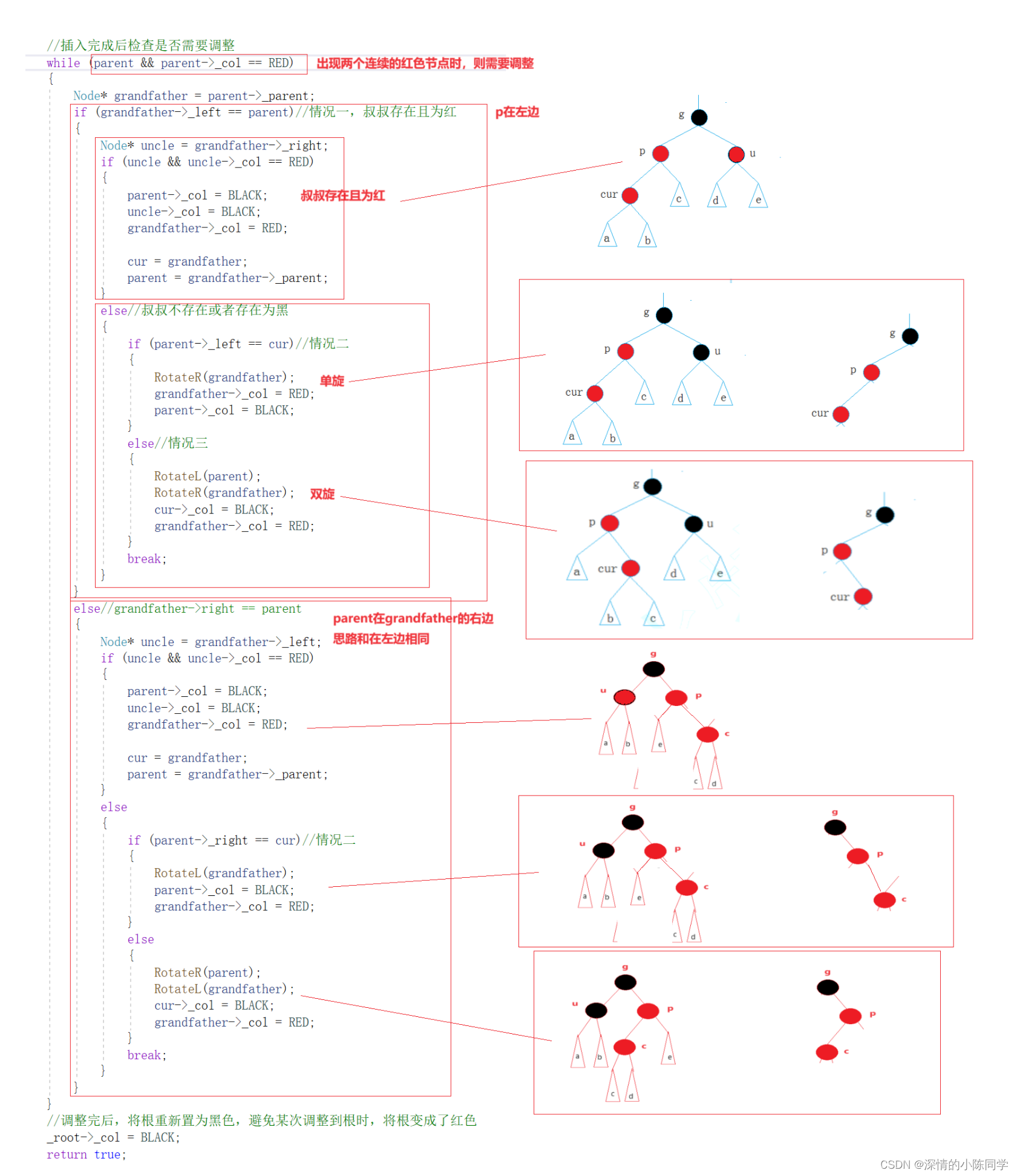
4.具体代码
bool Insert(const T& data)
{
if (_root == nullptr)
{
_root = new Node(data);
_root->_col = BLACK;
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (data < cur->_data)
{
parent = cur;
cur = cur->_left;
}
else if (data > cur->_data)
{
parent = cur;
cur = cur->_right;
}
else if (data == cur->_data)
{
return false;
}
}
cur = new Node(data);
if (data < parent->_data)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
//插入完成后检查是否需要调整
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
if (grandfather->_left == parent)//情况一,叔叔存在且为红
{
Node* uncle = grandfather->_right;
if (uncle && uncle->_col == RED)
{
parent->_col = BLACK;
uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = grandfather->_parent;
}
else//叔叔不存在或者存在为黑
{
if (parent->_left == cur)//情况二
{
RotateR(grandfather);
grandfather->_col = RED;
parent->_col = BLACK;
}
else//情况三
{
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else//grandfather->right == parent
{
Node* uncle = grandfather->_left;
if (uncle && uncle->_col == RED)
{
parent->_col = BLACK;
uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = grandfather->_parent;
}
else
{
if (parent->_right == cur)//情况二
{
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
//调整完后,将根重新置为黑色,避免某次调整到根时,将根变成了红色
_root->_col = BLACK;
return true;
}五、测试接口
在实现完Insert接口后,我们需要实现一些用于测试的接口,验证是否为红黑树
中序遍历InOrder
首先是提供一个中序遍历,但中序遍历只能验证是否是搜索二叉树,并不能保证一定是红黑树
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(const Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_data << " ";
_InOrder(root->_right);
}验证红黑树IsBalance
验证是否是红黑树,取决于树是否遵循着红黑树的规则,因此我们需要根据规则去写个函数去检查树是否为红黑树
//测试是否为红黑树
bool IsBalance()
{
if (_root->_col == RED)
{
return false;
}
int Reference = -1;
return _Check(_root,0,Reference);
}
//1.不能有连续的红色节点
//2.每条路径的黑色节点要数量相同
bool _Check(const Node* root,int black_num,int& Reference)
{
if (root == nullptr)
{
if (Reference == -1)//由第一次走完的路径作为参考值
{
Reference = black_num;
}
else if (Reference != black_num)//当存在黑色节点数量与参考值不同的路径时,说明违反规则
{
return false;
}
return true;
}
//当如果节点为红,则检查父母节点是否也为红,若是红则违反规则
if (root->_col == RED && root->_parent && root->_parent->_col == RED)
{
return false;
}
//统计每条路径的黑色节点,当走到空时则说明该路径走完
if (root->_col == BLACK)
{
black_num++;
}
return _Check(root->_left,black_num,Reference) && _Check(root->_right,black_num,Reference);
}
};总结
本章模拟实现了红黑树的核心部分,提供了测试接口,下一篇将会把红黑树进行一些改造,并且完整红黑树的部分基本接口,用于封装set和map,并且将模拟实现对set和map的封装