1. 题目链接:37. 解数独
2. 题目描述:
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
- 数字
1-9在每一行只能出现一次。- 数字
1-9在每一列只能出现一次。- 数字
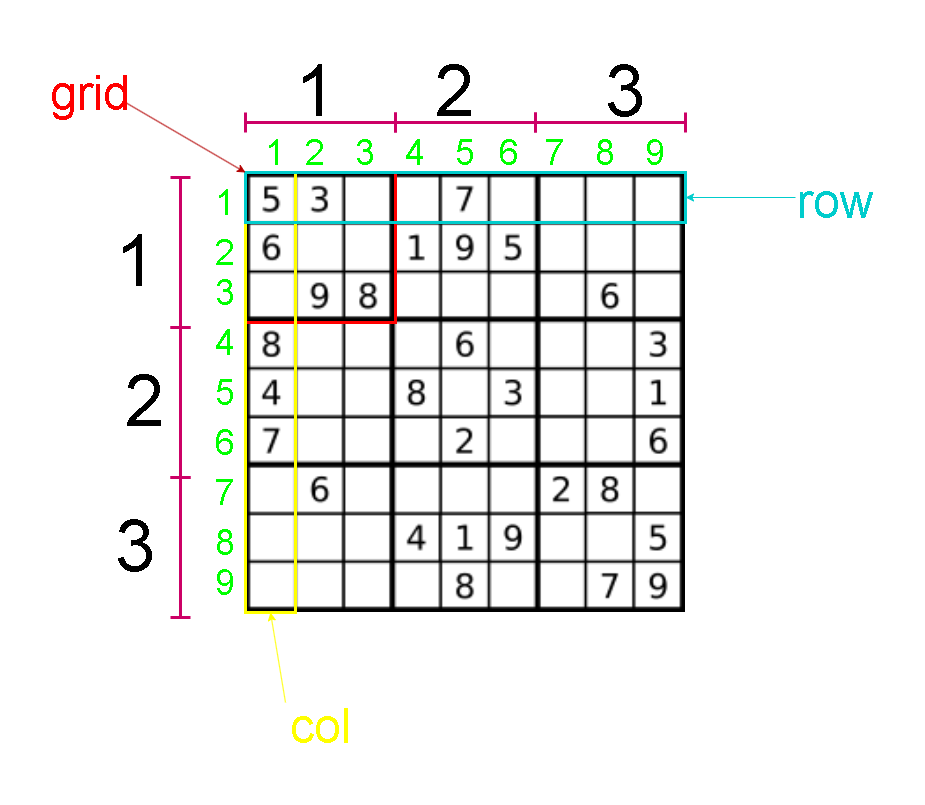
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)数独部分空格内已填入了数字,空白格用
'.'表示。示例 1:
输入:board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]] 输出:[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]] 解释:输入的数独如上图所示,唯一有效的解决方案如下所示:
提示:
board.length == 9board[i].length == 9board[i][j]是一位数字或者'.'- 题目数据 保证 输入数独仅有一个解
3. 解法:
3.1 算法思路:
为了存储每个位置的元素,我们需要定义一个二维数组。首先,我们记录所有已知的数据,然后遍历所有需要处理的位置,并遍历数字1~9。为了每个位置,我们检查该数字是否已经存放在该位置,同时检查行、列和九宫格是否唯一。
我们可以用一个二维数组来记录每个数字在每一行中是否出现,一个二维数组记录每个数字在每一列中是否出现。对于九宫格,我们可以以行和列除以3得到的商作为九宫格的坐标,并使用一个三维数组来记录每个数字在每一个九宫格中是否出现。在检查是否存在冲突时,只需检查行、列和九宫格里对应的数字是否已被标记。如果数字至少有一个位置(行、列、九宫格)被标记,则存在冲突,因此不能在该位置放置当前数字。
特别地,在本题中,我们需要直接修改给出的数组,因此在找到一种可行的方法时,应该停止递归,以防正确的方法被覆盖。
3.2 初始化定义:
- 定义行、列、九宫格标记数组已经找到可行方法的标记变量,将它们初始化为false
- 定义一个数组来存储每个需要处理的位置
- 将题目给出的所有元素的行、列以及九宫格坐标标记为true
- 将所有需要处理的位置存入数组
3.3 递归流程:
- 结束条件:已经处理完所有需要处理的元素。如果找到了可行的解决方案,则将标记变量更新为true并返回
- 获取当前需要处理的元素的行列值
- 遍历1~9。如果当前数字可以填入当前位置,并且标记变量未被赋值为true,则将当前位置的行、列以及九宫格标记为true,将当前数字赋值给board数组中的相应位置元素,然后对下一个位置进行递归。
- 递归结束时,撤回标记。
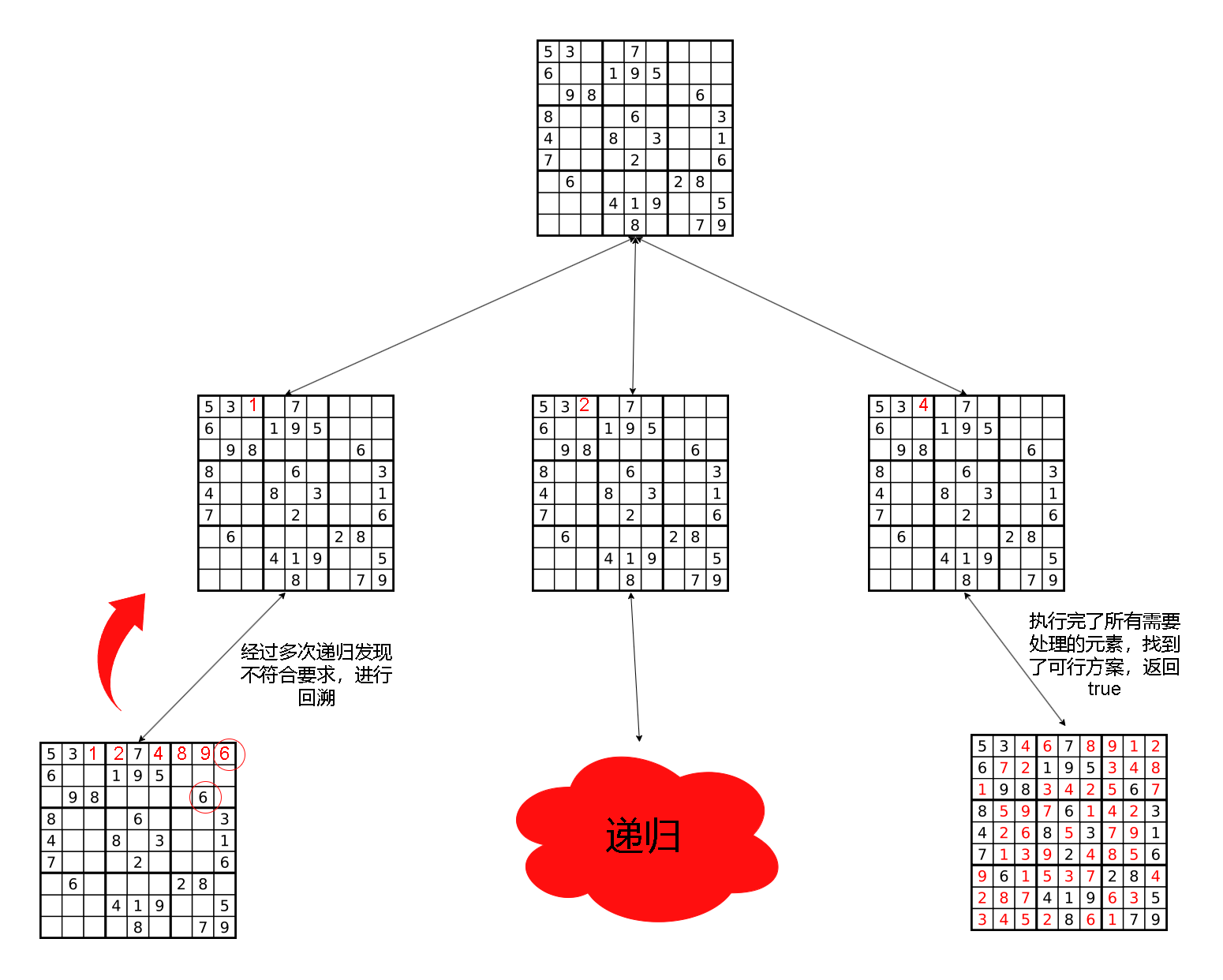
3.4 C++算法代码:
class Solution {
bool row[9][10], col[9][10], gird[3][3][10];
public:
// 解决数独问题的主函数
void solveSudoku(vector<vector<char>>& board)
{
// 初始化行、列和宫格的标记数组
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (board[i][j] != '.') {
int num = board[i][j] - '0';
row[i][num] = col[j][num] = gird[i / 3][j / 3][num] = true;
}
}
}
// 调用深度优先搜索函数进行数独求解
dfs(board);
}
// 深度优先搜索函数
bool dfs(vector<vector<char>>& board)
{
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (board[i][j] == '.') {
for (int num = 1; num <= 9; num++) {
if (!row[i][num] && !col[j][num] && !gird[i / 3][j / 3][num]) {
// 将数字填入空格中,并更新行、列和宫格的标记数组
board[i][j] = '0' + num;
row[i][num] = col[j][num] = gird[i / 3][j / 3][num] = true;
// 递归调用深度优先搜索函数,继续填充下一个空格
if (dfs(board) == true) return true;
// 如果填充失败,回溯到上一个空格,清空该空格,并更新行、列和宫格的标记数组
board[i][j] = '.';
row[i][num] = col[j][num] = gird[i / 3][j / 3][num] = false;
}
}
return false;
}
}
}
return true; // 所有空格都已被正确填充,数独问题解决
}
};