大家好,我是带我去滑雪!
利用神经网络解决组合优化问题是神经网络应用的一个重要方面。所谓组合优化问题,就是在给定约束条件下,使目标函数极小(或极大)的变量组合问题。将Hopfield网络应用于求解组合优化问题,把目标函数转化为网络的能量函数,把问题的变量对应到网络的状态,这样,当网络的能量函数收敛于极小值时,问题的最优解也随之求出。由于神经网络是并行计算的,其计算量不随维数的增加而发生指数性“爆炸”,因而对于组合优化问题的高速计算特别有效。典型的组合优化问题有旅行商问题、0-1背包问题、装箱问题、图着色问题、聚类问题等问题。这些问题的描述都非常简单,但优化求解很困难,其主要原因是求解这些问题的算法运行时,需要极长的运行时间和极大的存储空间。
本期使用连续Hopfield神经网络实现旅行商问题优化计算。
一、问题与模型设计
(1)问题描述
旅行商问题,(Traveling Saleman Problem,TSP)是VRP的特例,由于Gaery[1]已证明TSP问题是NP难题,因此,VRP也属于NP难题。旅行商问题(TSP)又译为旅行推销员问题、货郎担问题,简称为TSP问题,是最基本的路线问题,该问题是在寻求单一旅行者由起点出发,通过所有给定的需求点之后,最后再回到原点的最小路径成本。
现对于一个城市数量为10的TSP问题,要求设计一个可以对其组合优化的连续型Hopfield神经网络模型,利用改模型可以快速地找到最优(或者近似最优)的一条路线。
(2)模型建立思路
由于连续型Hopfield神经网络具有优化计算的特性,因此将TSP问题的目标函数(即最短路径)与网络的能量函数相对应,将经过的城市顺序与网络的神经元状态相对应。这样,由连续型Hopfield神经网络的稳定性定理知,当网络的能量函数趋于最小值时,网络的神经元状态也趋于平衡点,此时对应的城市顺序即为最佳的路线。
(3)设计步骤
模型映射:为了将TSP问题映射为一个神经网络的动态过程,Hopfield神经网络采取换位矩阵的表示方式,用NxN的矩阵表示商人访问N个城市。对于N个城市TSP问题,使用NxN个神经元来实现,而每行每列只能有一个1,其余都是0,矩阵中1的和为N,该矩阵成为换位矩阵。
构造网络能量函数和动态方程:设计的Hopfield神经网络的能量函数与目标函数(即最短路径)相对应的。同时,考虑到有效解的实际意义,即换位矩阵的每行每列都只能有一个1。因此,网络的能量函数包含目标项和约束项两部分。
初始化网络:Hopfield神经网络迭代过程对网络的能量函数及动态方程的系数十分敏感,在总结前人经验及多次实验的基础上,网络输入初始化选取如下:A=200,D=100,采样时间设置为0.0001,迭代次数为10000。
优化计算:当网络的结果及参数设计完成后,迭代优化计算的过程就变得非常简单,具体步骤:
步骤1:导入N个城市的位置坐标并计算城市之间的距离;
步骤2:网络初始化;
步骤3:计算能量函数;
步骤4:判断迭代次数是否结束,若迭代次数大于10000,则终止。
二、代码实现
(1)清空环境变量、声明全局变量
clear all
clc
global A D(2)城市位置导入并计算城市间距离
load city_location
distance = dist(citys,citys');(3)初始化网络
N = size(citys,1);
A = 200;
D = 100;
U0 = 0.1;
step = 0.0001;
delta = 2 * rand(N,N) - 1;
U = U0 * log(N-1) + delta;
V = (1 + tansig(U/U0))/2;
iter_num = 10000;
E = zeros(1,iter_num);(4)寻优迭代
寻优迭代过程包括动态方程计算、输入神经元状态更新、输出神经元状态更新、能量函数计算四个步骤。
for k = 1:iter_num
dU = diff_u(V,distance);
U = U + dU*step;
V = (1 + tansig(U/U0))/2;
e = energy(V,distance);
E(k) = e;
end(5)动态方程计算
function du=diff_u(V,d)
global A D
n=size(V,1);
sum_x=repmat(sum(V,2)-1,1,n);
sum_i=repmat(sum(V,1)-1,n,1);
V_temp=V(:,2:n);
V_temp=[V_temp V(:,1)];
sum_d=d*V_temp;
du=-A*sum_x-A*sum_i-D*sum_d;(6)能量函数计算
function E=energy(V,d)
global A D
n=size(V,1);
sum_x=sumsqr(sum(V,2)-1);
sum_i=sumsqr(sum(V,1)-1);
V_temp=V(:,2:n);
V_temp=[V_temp V(:,1)];
sum_d=d*V_temp;
sum_d=sum(sum(V.*sum_d));
E=0.5*(A*sum_x+A*sum_i+D*sum_d);(7)主函数
[rows,cols] = size(V);
V1 = zeros(rows,cols);
[V_max,V_ind] = max(V);
for j = 1:cols
V1(V_ind(j),j) = 1;
end
C = sum(V1,1);
R = sum(V1,2);
flag = isequal(C,ones(1,N)) & isequal(R',ones(1,N));
%% 结果显示
if flag == 1
% 计算初始路径长度
sort_rand = randperm(N);
citys_rand = citys(sort_rand,:);
Length_init = dist(citys_rand(1,:),citys_rand(end,:)');
for i = 2:size(citys_rand,1)
Length_init = Length_init+dist(citys_rand(i-1,:),citys_rand(i,:)');
end
% 绘制初始路径
figure(1)
plot([citys_rand(:,1);citys_rand(1,1)],[citys_rand(:,2);citys_rand(1,2)],'o-')
for i = 1:length(citys)
text(citys(i,1),citys(i,2),[' ' num2str(i)])
end
text(citys_rand(1,1),citys_rand(1,2),[' 起点' ])
text(citys_rand(end,1),citys_rand(end,2),[' 终点' ])
title(['优化前路径(长度:' num2str(Length_init) ')'])
axis([0 1 0 1])
grid on
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
% 计算最优路径长度
[V1_max,V1_ind] = max(V1);
citys_end = citys(V1_ind,:);
Length_end = dist(citys_end(1,:),citys_end(end,:)');
for i = 2:size(citys_end,1)
Length_end = Length_end+dist(citys_end(i-1,:),citys_end(i,:)');
end
disp('最优路径矩阵');V1
% 绘制最优路径
figure(2)
plot([citys_end(:,1);citys_end(1,1)],...
[citys_end(:,2);citys_end(1,2)],'o-')
for i = 1:length(citys)
text(citys(i,1),citys(i,2),[' ' num2str(i)])
end
text(citys_end(1,1),citys_end(1,2),[' 起点' ])
text(citys_end(end,1),citys_end(end,2),[' 终点' ])
title(['优化后路径(长度:' num2str(Length_end) ')'])
axis([0 1 0 1])
grid on
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
% 绘制能量函数变化曲线
figure(3)
plot(1:iter_num,E);
ylim([0 2000])
title(['能量函数变化曲线(最优能量:' num2str(E(end)) ')']);
xlabel('迭代次数');
ylabel('能量函数');
else
disp('寻优路径无效');
end(8)结果输出
优化前的路径:

优化后的路径图:

优化后的路径距离相比于没有优化的路径距离更短。
能量函数变化曲线:
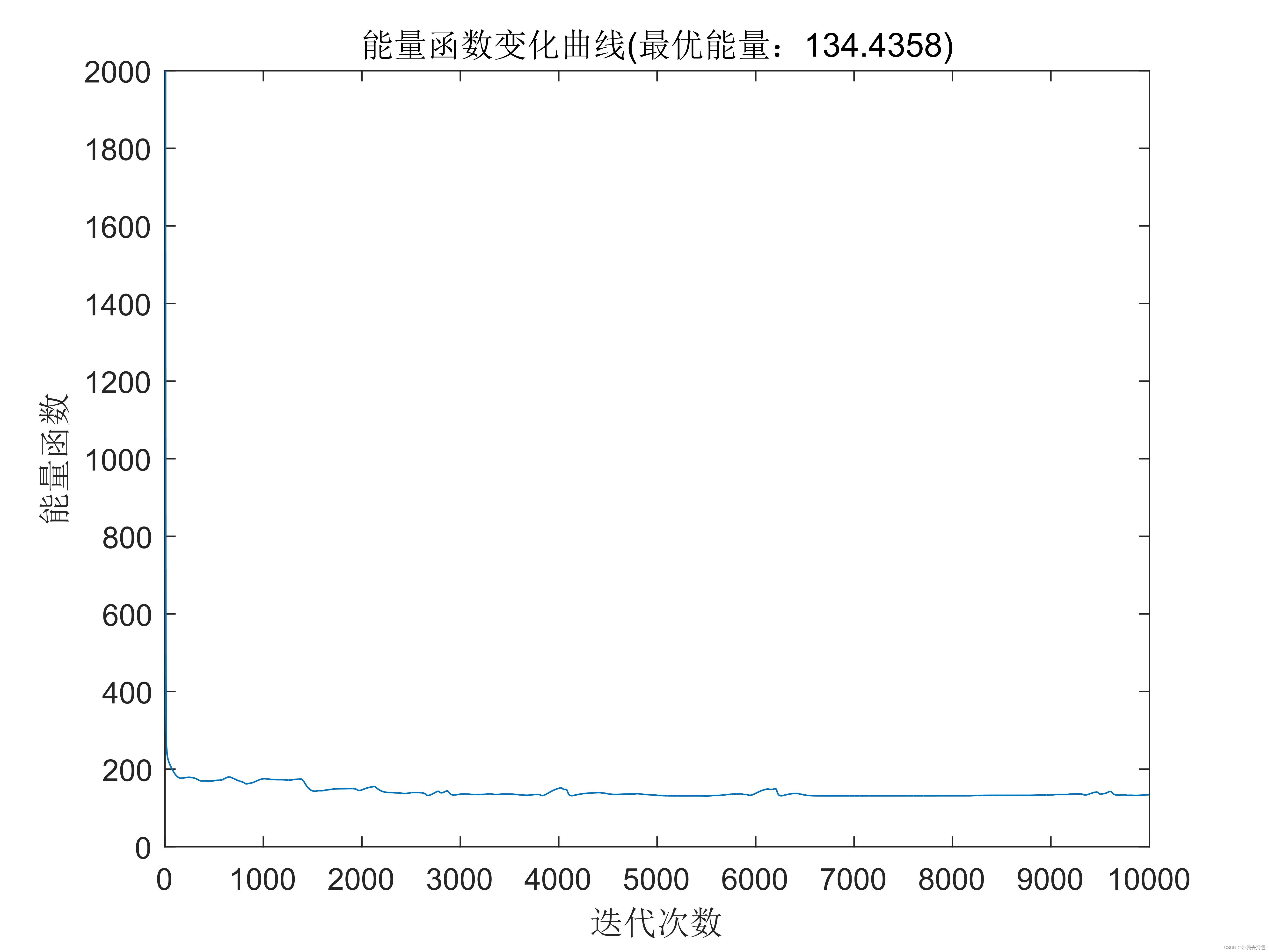
结果表明:利用Hopfield神经网络 ,可以快速准确地解决TSP问题。同理,对于其他利用枚举法会产生“组合爆炸”的组合优化问题,利用连续型Hopfield神经网络也可以进行优化计算。
需要数据集的家人们可以去百度网盘(永久有效)获取:
链接:
提取码:2138
更多优质内容持续发布中,请移步主页查看。
点赞+关注,下次不迷路!