它原本是日本学者为了质量管理而设计的试验。后来被用在算法的参数设计上,可以利用部分的试验确定出最合理的参数组合。
举个例子,比如遗传算法中的种群数pop,交叉概率pr,变异概率pm,以及迭代次数N,每个参数我们初始定为3个值,那么想要确定最优的参数组合需要设计3^4=81次试验,才能确定下来。这样的试验规模太大了,采用正交试验的方法只需要进行L27=L3^4(3水平4因子),27次试验就可以确定出最优的参数组合。
再来说一下它的核心:不必进行全部组合试验,而只需要进行部分组合的试验,就可以确定最优的参数组合。
那么问题就转变为:
(1)挑选出哪些部分的组合?
(2)怎么根据部分组合的信息最终取反推出最优的组合信息(不是所有组合都进行了试验,那么那些没出现的组合试验我们怎么去评估结果;以及因为试验和结果不是一对一的关系,我们怎么反推出最优?)
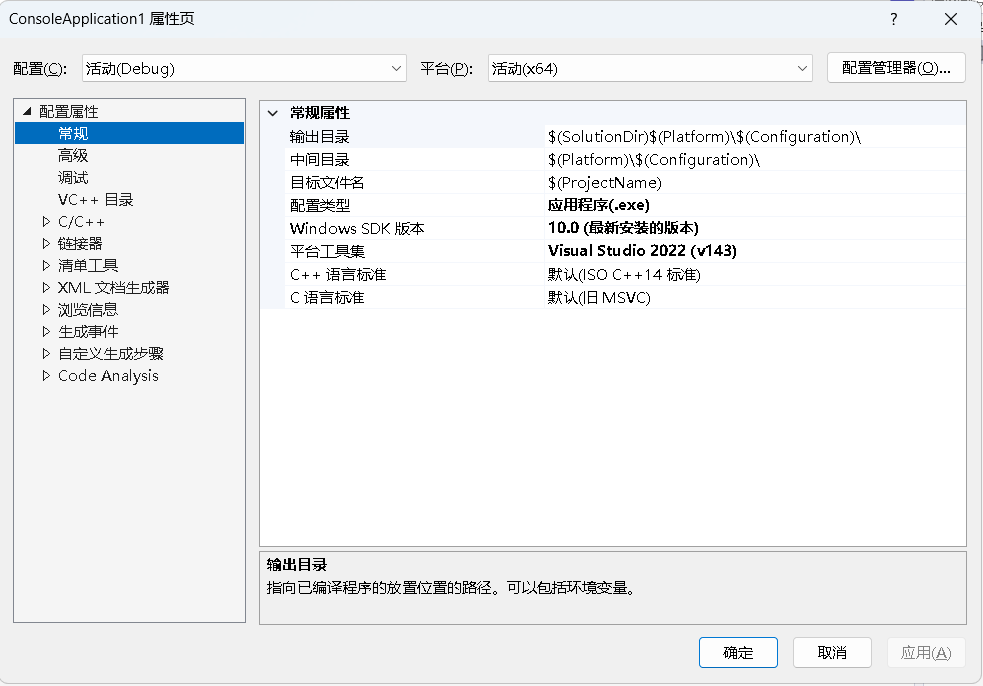
下面以Minitab软件为例——Minitab田口设计,对上面两个问题进行解答。别的软件或在线网址也可以实现,原理相通,操作有些微差别。
1.挑选出部分组合
这是DOE的设计部分,软件可以自己生成对应的组合。

这里我们需要挑选的是,因子数,以及因子水平数。因子数就是哪些参数,参数的数量;因子水平数是每个参数有多少种取值。一开始举的例子中,因子数是4个,分别是pop,pr,pm,以及N。因子水平数是3个,分别取不同的值,比如pop=20、50、100等。
最终体现在论文中,以及软件中的是L27(试验的次数为27)或者是L3^4(3水平4因子)。
也可以修改设计,改变名称、因子水平值等。最终表里面不显示1、2、3、4显示具体的值,比如pr=0.5、0.6、07、0.8等。
2.选最优组合
具体操作可以看这篇文章:DOE实验设计之田口方法含minitab应用 - 知乎 (zhihu.com)
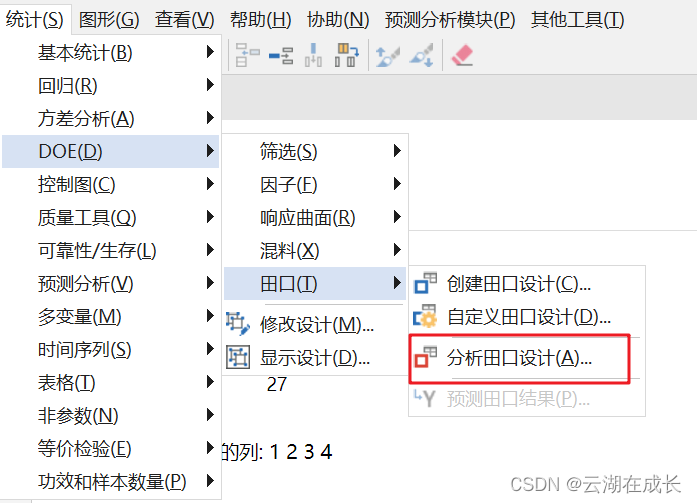
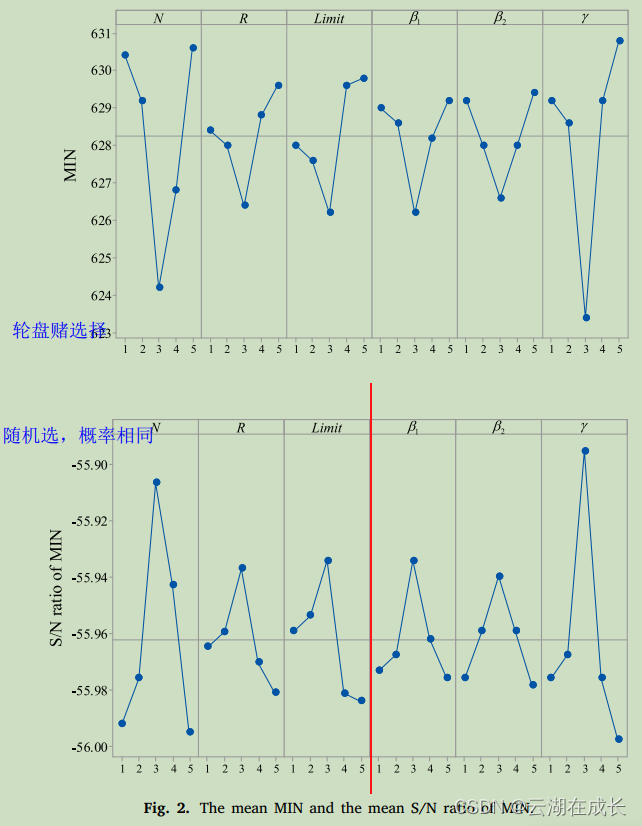
我们需要的是最终的组合。等我们进行过27次试验后,会生成两个图。一个是信噪比(S/N,分为望目望大望小),该比值越大,表明品质越好;一个是均值,我们经常做最小化问题,是越小越好。
| 望大 | 使响应最大化 | 正 | S/N = −10 *log(Σ(1/Y2)/n) |
| 望目 | 以响应为目标且要使信噪比只以标准差为基础 | 正、零或负 | S/N = −10 *log(σ2) |
| 望目(默认) | 以响应为目标且要使信噪比以均值和标准差为基础 | 具有“绝对零”的非负数,其中在均值为零时标准差为零 |
调整后的公式为:
|
| 望小 | 使响应最小化 | 目标值为零的非负数 | S/N = −10 *log(Σ(Y2)/n)) |
最终可以根据信噪比和均值,得到最终的组合,并且可以得到因子的重要性排序(根据秩排序)。
如,下面这张图,可以确定最终的参数组合取值,N为第3水平,R为第三水平,Limit为第三水平,β1&β2&γ都为第三水平。