目录
- 参考
- 一、Attention注意力机制
- 原理
- 计算过程
- 二、自注意力机制
- 2.1 自注意力关键!!
- 2.2 实现步骤
- 1. 获取 K Q V
- 2. MatMul
- 3. scale + softmax归一化
- 4. MalMul
- 2.3 自注意力机制的缺陷
- 三、多头自注意力机制
- 3.1 简介
- 3.2 实现步骤
- 3.3 公式
参考
感谢我的互联网导师:水论文的程序猿
参考资料和图片来源:
Transformer、GPT、BERT,预训练语言模型的前世今生
【Transformer系列(2)】注意力机制、自注意力机制、多头注意力机制、通道注意力机制、空间注意力机制超详细讲解
【Deformable DETR 论文+源码解读】Deformable Transformers for End-to-End Object Detection
一、Attention注意力机制
原理
我(查询q) 看-> 一张图 ( 被查询对象v )
我看这张图,第一眼,我就会去判断哪些东西对我而言更重要,哪些对我而言又更不重要(去计算 Q 和 V 里的事物的重要度)
重要度计算,其实是不是就是相似度计算(更接近),点乘其实是求内积。
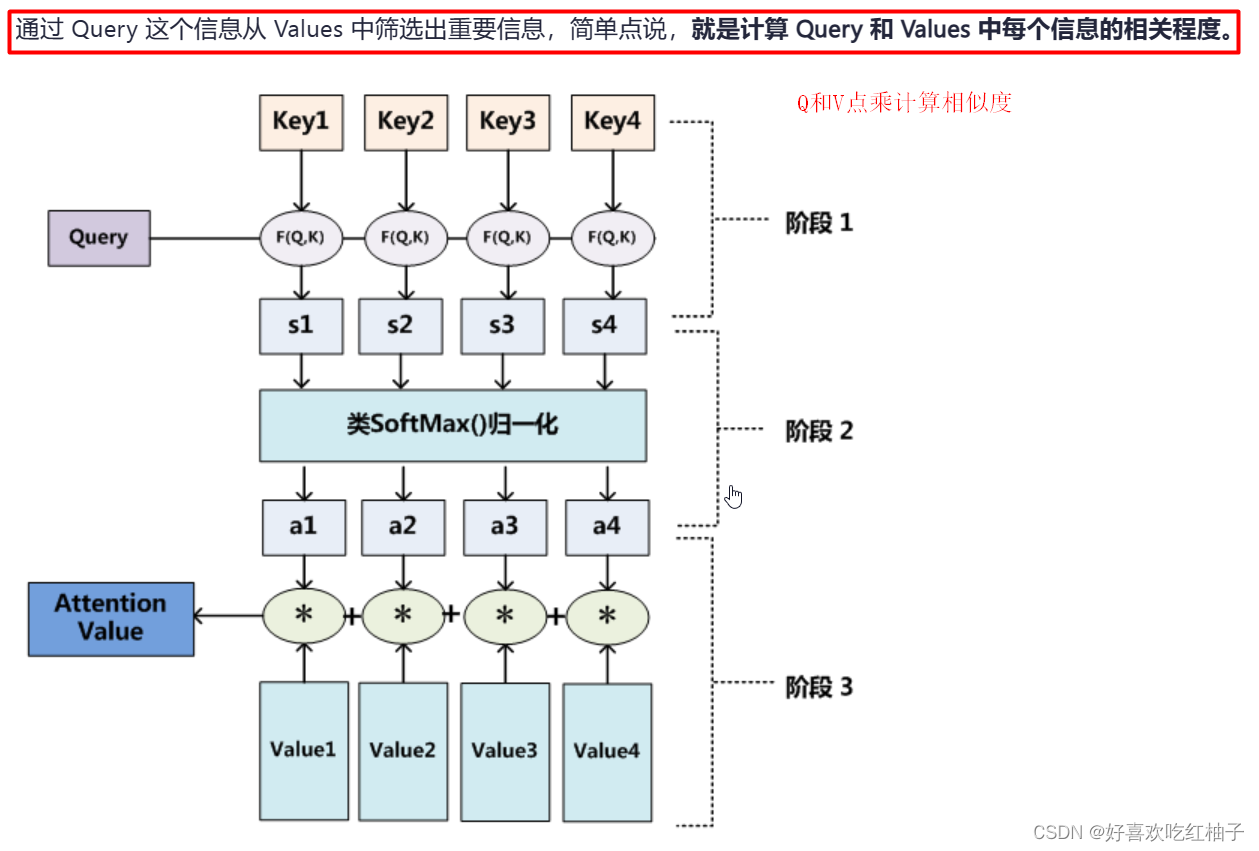
计算过程
被查询对象: V = ( v 1 , v 2 , v 3 , . . . ) V = (v1, v2, v3, ...) V=(v1,v2,v3,...)
在transformer中,K == V
-
计算相似度: Q ∗ k 1 , Q ∗ k 2 , . . . . . . = s 1 , s 2 , . . s n . Q*k1 , Q*k2, ...... = s1, s2, ..sn. Q∗k1,Q∗k2,......=s1,s2,..sn.
-
归一化求概率: s o f t m a x ( s 1 , s 2 , s 3 , . . . ) = a 1 , a 2 , a 3 , . . a n . softmax(s1, s2, s3, ...) = a1, a2, a3, ..an. softmax(s1,s2,s3,...)=a1,a2,a3,..an.
-
更新V为V’: V ′ = ( a 1 ∗ v 1 + a 2 ∗ v 2 + . . . + a n ∗ v n ) V' = (a1*v1+a2*v2+...+an*vn) V′=(a1∗v1+a2∗v2+...+an∗vn)
这样就会就得到一个新的 V’,用 V’ 代替 V。这个新的 V’除了能表示K和V(K==V),还能代表Q的信息(对Q而言对K中哪个部分关注最多,最重要),找出来了Q对K的注意力集中在哪里。
二、自注意力机制
2.1 自注意力关键!!
K、 V、 Q 来自于同一个X,三者同源。所以叫做自注意力
K V Q 如何得到? 通过x与三个向量参数( W K , W V , W Q W^K, W^V, W^Q WK,WV,WQ)相乘得到。这三个参数向量也是我们要学习的东西。
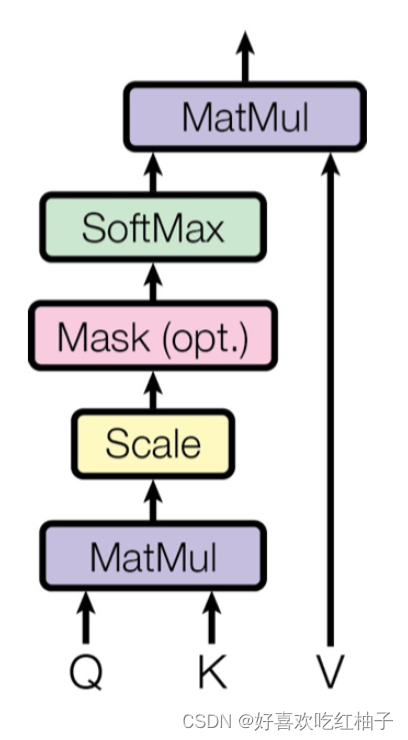
2.2 实现步骤
1. 获取 K Q V
有一个句子是“
T
h
i
n
k
i
n
g
M
a
c
h
i
n
e
s
”,该句子中有两个单词,两个单词的向量分别
x
1
,
x
2
,分别与(
W
K
,
W
V
,
W
Q
)
3
个矩阵相乘得到
q
1
,
q
2
,
k
1
,
k
2
,
v
1
,
v
2
的
6
个向量。
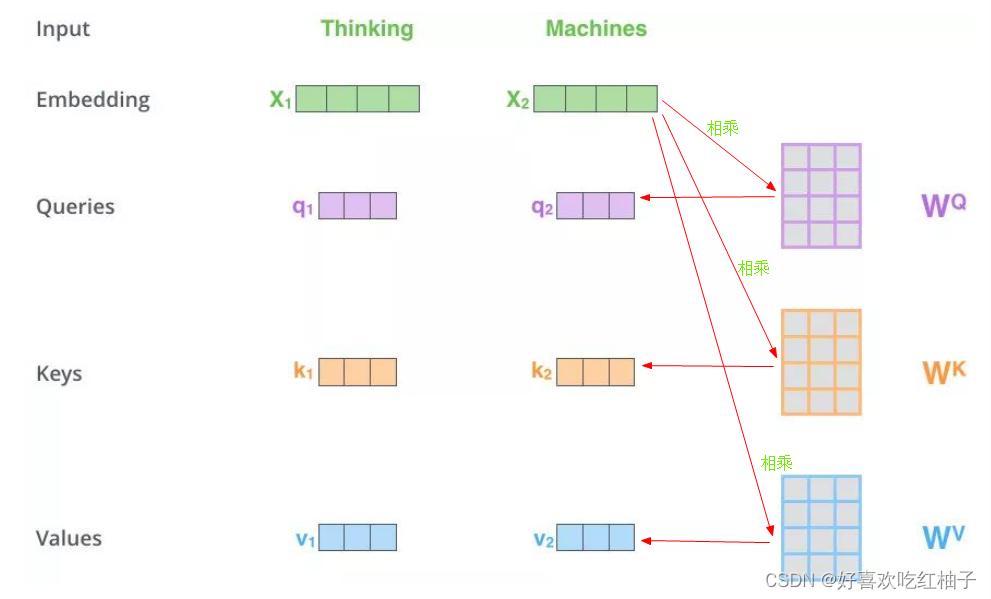
有一个句子是“Thinking Machines”,该句子中有两个单词,两个单词的向量分别x1,x2,分别与(W^K, W^V, W^Q)3个矩阵相乘得到q1,q2,k1,k2,v1,v2的6个向量。
有一个句子是“ThinkingMachines”,该句子中有两个单词,两个单词的向量分别x1,x2,分别与(WK,WV,WQ)3个矩阵相乘得到q1,q2,k1,k2,v1,v2的6个向量。
2. MatMul
q
1
分别与
k
1
,
k
2
点乘得到得分,寻找
q
1
对
x
1
,
x
2
的重要信息
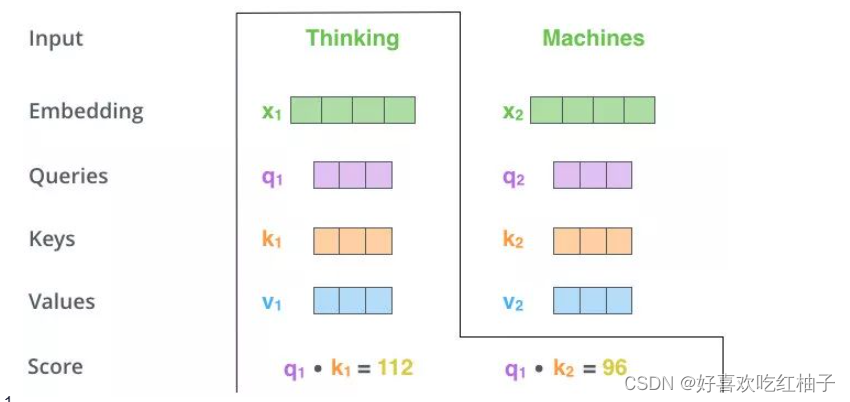
q1分别与k1,k2点乘得到得分,寻找q1对x1,x2的重要信息
q1分别与k1,k2点乘得到得分,寻找q1对x1,x2的重要信息
3. scale + softmax归一化
scale:对得分进行规范,防止梯度下降出现问题。
softmax: 归一化求概率得到a1,a2
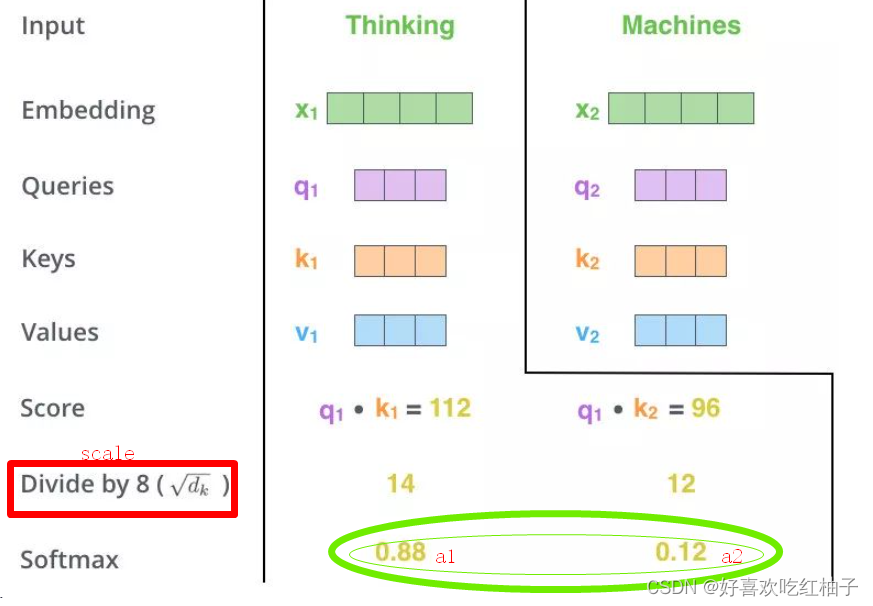
经过Softmax的归一化后,每个值是一个大于0且小于1的权重系数,且总和为0,这个结果可以被理解成一个权重矩阵W。
这个W就是注意力权重,其中包含着该单词与该句子之间的相关信息和更关心哪个部分。
4. MalMul
用得分比例 [0.88,0.12] 乘以[ v 1 , v 2 v1,v2 v1,v2]后得到相加得到z1 : z 1 = ( a 1 ∗ v 1 + a 1 ∗ v 2 ) z1 = (a1 * v1 + a1*v2) z1=(a1∗v1+a1∗v2)
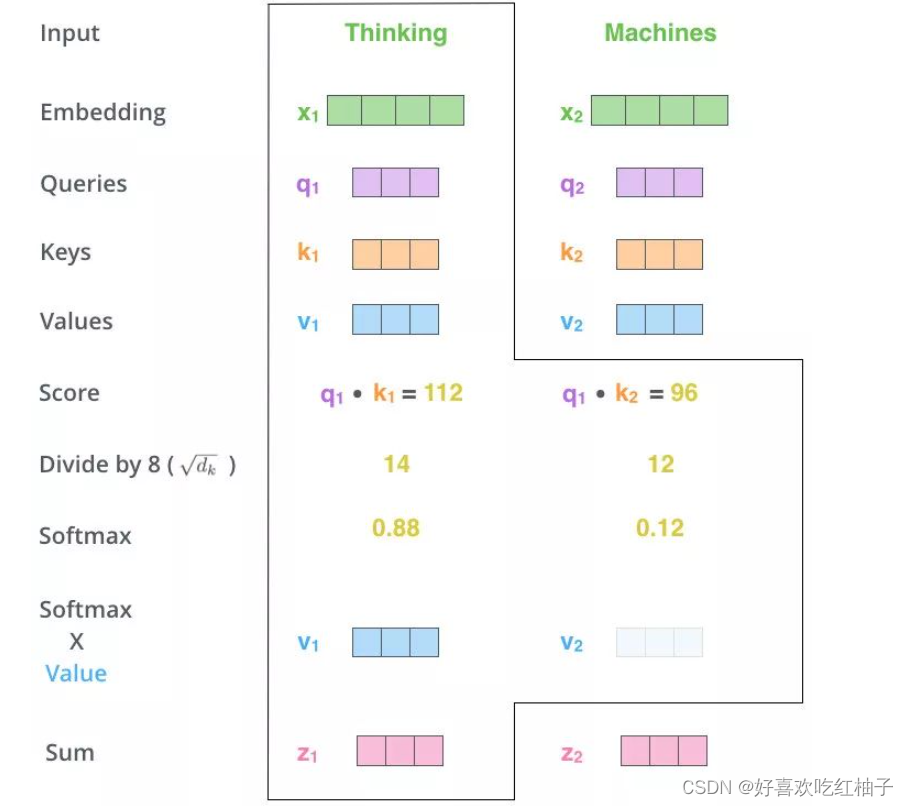
得到的新向量z1就是thinking这个单词的新的词向量,z1里面包含着thinking这个单词和“Thinking Machines”这句话里每一个单词的相似程度和关联信息。
同理可得到z2向量,代表machines的新的词向量。
2.3 自注意力机制的缺陷
- 自注意力机制虽然考虑了所有的输入向量,但没有考虑到向量的位置信息。在实际的文字处理问题中,可能在不同位置词语具有不同的性质,比如动词往往较低频率出现在句首。(解决:引入位置编码)
- 模型在对当前位置的信息进行编码时,会过度的将注意力集中于自身的位置,有效信息抓取能力就差一些。 (解决:引入多头注意力)
三、多头自注意力机制
3.1 简介
简单理解:多组自注意力机制并行运行,最后把结果拼接起来。

3.2 实现步骤
- 定义多组 W q 、 W k 和 W v Wq、Wk和Wv Wq、Wk和Wv,生成多组Q、K和V
- 分别对多组进行自注意力机制,得到多组 z ( z 0 − z n z(z_0-z_n z(z0−zn)
- 多组
z
(
z
0
−
z
n
z(z_0-z_n
z(z0−zn)进行拼接(cancat),再乘以矩阵W做一次线性变化降低维度,得到最终的Z。
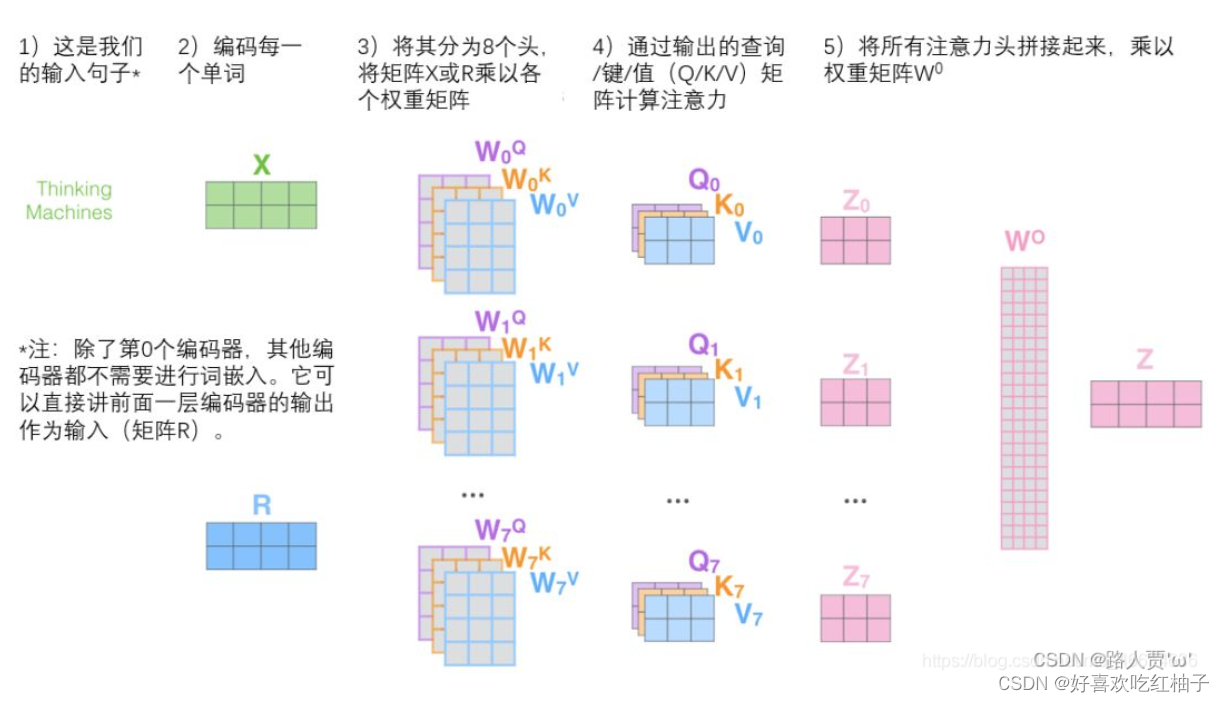
3.3 公式
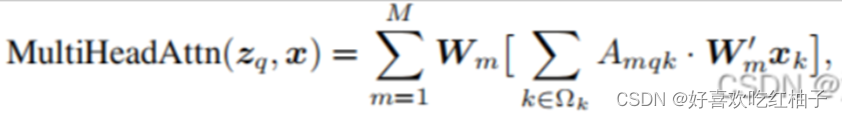
其中,x是输入特征,z表示 query,由x经过Wq线性变换来的,k是key的索引,q 是query的索引,M 表示多头注意力的头数,m代表第几注意力头部,
A
m
q
k
A_{mqk}
Amqk表示第m头注意力权重(即上图a中一直到SoftMax的过程),
W
m
’
x
k
W^’_m x_k
Wm’xk其实就是value,整个[ ]内的过程就是图a的全过程,
W
m
W_m
Wm是注意力施加在value之后的结果经过线性变换(也就是图b的Linear)从而得到不同头部的输出结果,
Ω
k
\Omega_k
Ωk表示所有key的集合。