电路综合-基于简化实频的SRFT集总参数切比雪夫低通滤波器设计

6、电路综合-基于简化实频的SRFT微带线切比雪夫低通滤波器设计中介绍了使用微带线进行切比雪夫滤波器的设计方法，在此对集总参数的切比雪夫响应进行分析。

SRFT集总参数切比雪夫低通滤波器综合不再需要查表，直接从底层原理进行设计。

0、基本理论

参考-Design of Ultra Wideband Power Transfer Networks第十章的推导过程

n 次切比雪夫多项式定义为：

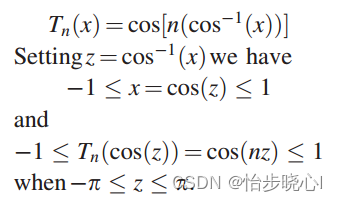
n在1到5时的切比雪夫多项式表：

此表可以使用下面的代码计算得出：

clear
clc
syms x
%定义切比雪夫阶数
n=1;
for n=1:1:9
T=(simplify(cos(n*acos(x))));
disp('----------------------------------------------------')
disp([num2str(n),'th Chebyshev polynomials is:']);disp(T);
end

代码的运行结果为：

1、设计步骤

切比雪夫的增益函数如下所示（其中的希腊字符是纹波因子，解释见6、电路综合-基于简化实频的SRFT微带线切比雪夫低通滤波器设计）：

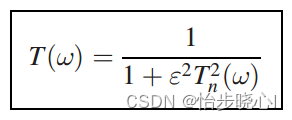
增益函数实际上就是S21，由此可以得到其网络对应的S11参数（下面的F11代表的就是S11,p=jw是Laplace因子）：

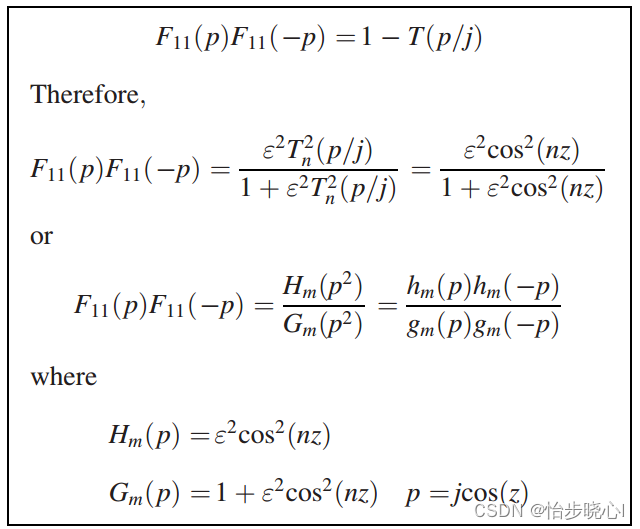
有公式S11=h( p)/g( p)，因此只有求得h( p)和g( p)就可以进行策动点阻抗的综合了。h( p)的求解基于H（p）的零点pr：

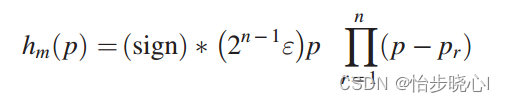
同理，g( p)的求解基于G（p）的零点pr：

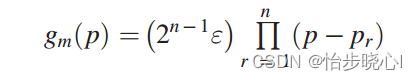
给出一个三阶的切比雪夫的gm的求解案例：

clear
clc
syms w
% p=jw
Gm=1+0.1*(4*(1j*w)^3-3*(1j*w))^2

simplify(Gm)
C = double(coeffs(Gm,w,"All"));
% 求Gm的根
roots(C)

syms lamda
g=(lamda+0.3320+1j*1.0395)*(lamda+0.3320-1j*1.0395)*(lamda+0.6639);
simplify(g);
% 求gm的系数
gm = double(coeffs(g,lamda,"All"))；

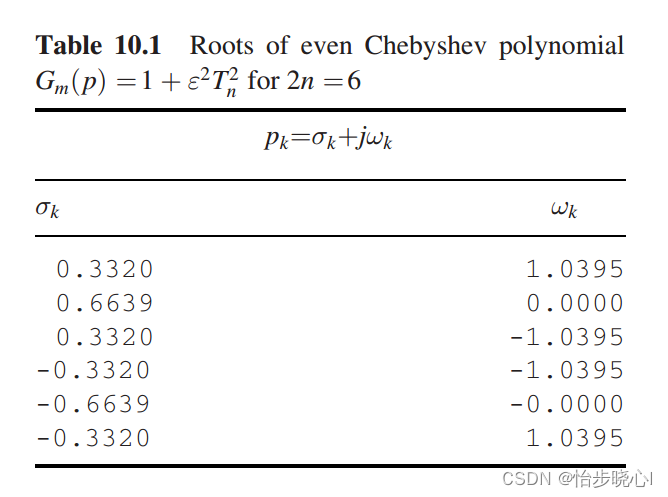
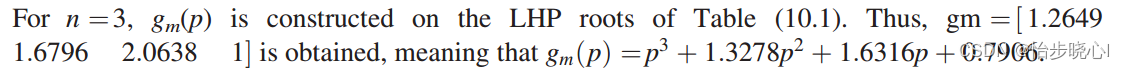
求到S11就可以计算出Zin，在此基础上使用梯形结构进行综合，一般的结构如下，其具体结构由h§前面的sign的符号决定，sign=1对应先电感，sign=-1对应先电容：

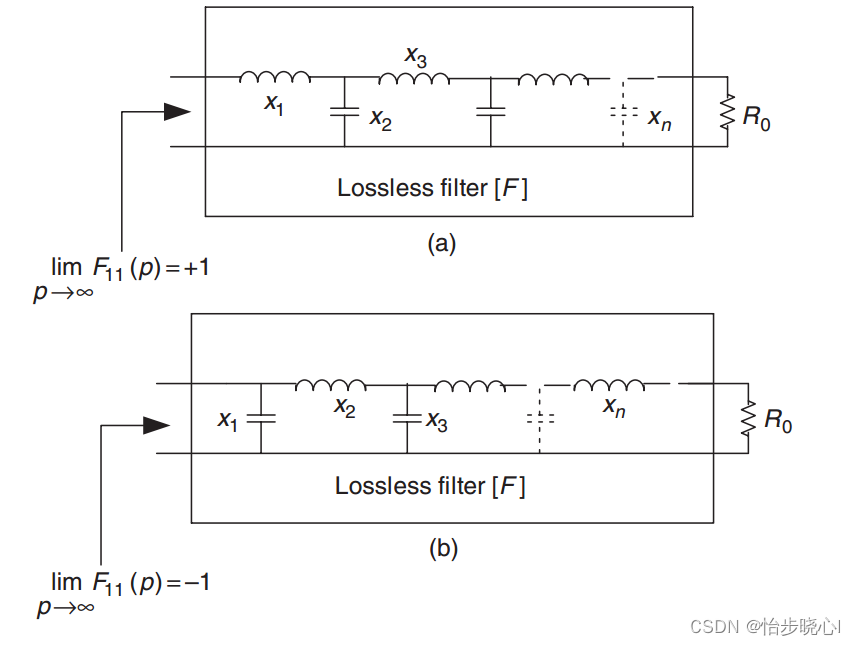
使用长除法进行综合：

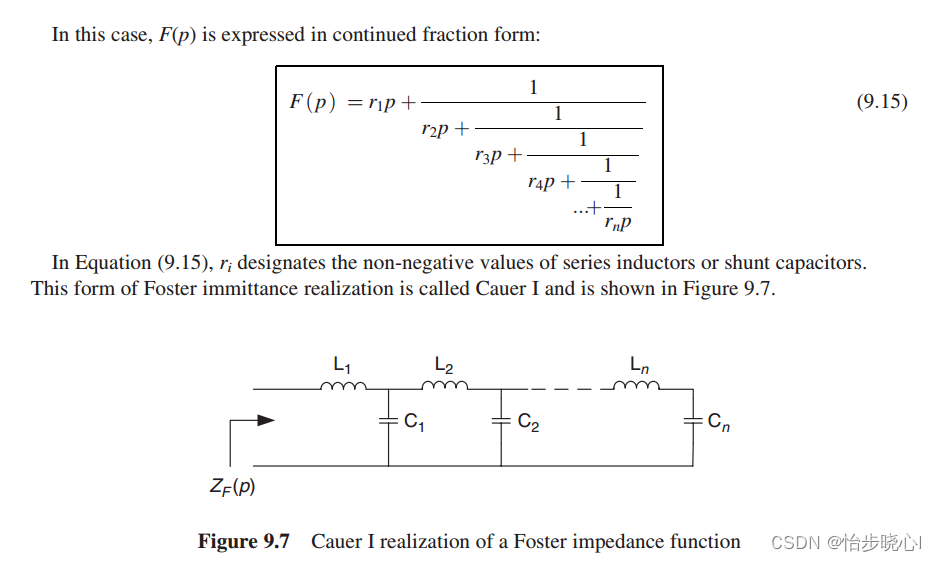
1、综合Matlab代码

主函数的代码，使用次代码不再需要查插入损耗表了

close all
clear
clc

% 设定通带波纹db
ILR=0.3;
% 设定切比雪夫滤波器阶数
n=3;
% 设定第一个元器件的类型+1和-1分别为电感和电容
sign=1;
% 设定端口阻抗
z0 = 50;	% set not to use normalization
% 设定截止频率
fc = 0.1e9;

eps_sq=10^(ILR/10)-1;
eps=sqrt(eps_sq);
beta=asinh(1/eps);
% Step 1: Generates the Explicit roots of Gm(p).
n2=2*n;
i=1;
j=sqrt(-1);
for k=0:(n2-1)
    x(k+1)=k;
    sig(k+1)=sin(pi*(2*k+1)/2/n)*sinh(beta/n);%Real{pk}
    omega(k+1)=cos(pi*(2*k+1)/2/n)*cosh(beta/n);%imag{pk}
    if(sig(k+1)<0) 
        p(i)=sig(k+1)+j*omega(k+1);%roots of g(p)
        i=i+1;
    end 
end
% Step 2: Construct gm(p)
gm=real(poly(p));%polynomial g(p)
%Step 3: Computation of hm(p)
for k=0:(n2-1)
x(k+1)=k;
    omega(k+1)=j*cos(pi*(2*k+1)/2/n);
end
for k=1:n
    ph(k)=omega(k);% Roots of hm(p)
end
hm=real(poly(-ph));%polynomial h(p)
hm=sign*hm;% h(p) with eps*Tn(1)

% Step 4: 求解TPG
NUM=gm+hm;
DEN=gm-hm;
syms w real
syms p
Zin=poly2sym(NUM,p)/poly2sym(DEN,p);
Zin=subs(Zin,p,1j*w);
R=real(Zin);X=imag(Zin);
TPG=4*R/((R+1)^2+X^2);

w_data=(0.01:0.01:2);
TPG=double(subs(TPG,w,w_data));
plot(w_data*fc/1e6,10*log10(TPG))
title("S21")
ylabel('S21')
xlabel('频率MHz')

% Step 4: 基于gm和hm进行综合
f0 = fc*2*pi;	% set not to use normalization
repcount = 0;	% synthesize all function
spi = 1;	% include poles at zero to synthesis
in_node = 1;	% define circuit input node
gr_node = 0;	% define circuit ground node
tol = 0.01;	% relative tolerance;
[CVal,CType,Eleman,node,pay2,payda2]=Synthesis_LongDiv(NUM,DEN,z0,f0,repcount,spi,in_node,gr_node,tol);
Plot_Circuit(CType,CVal);

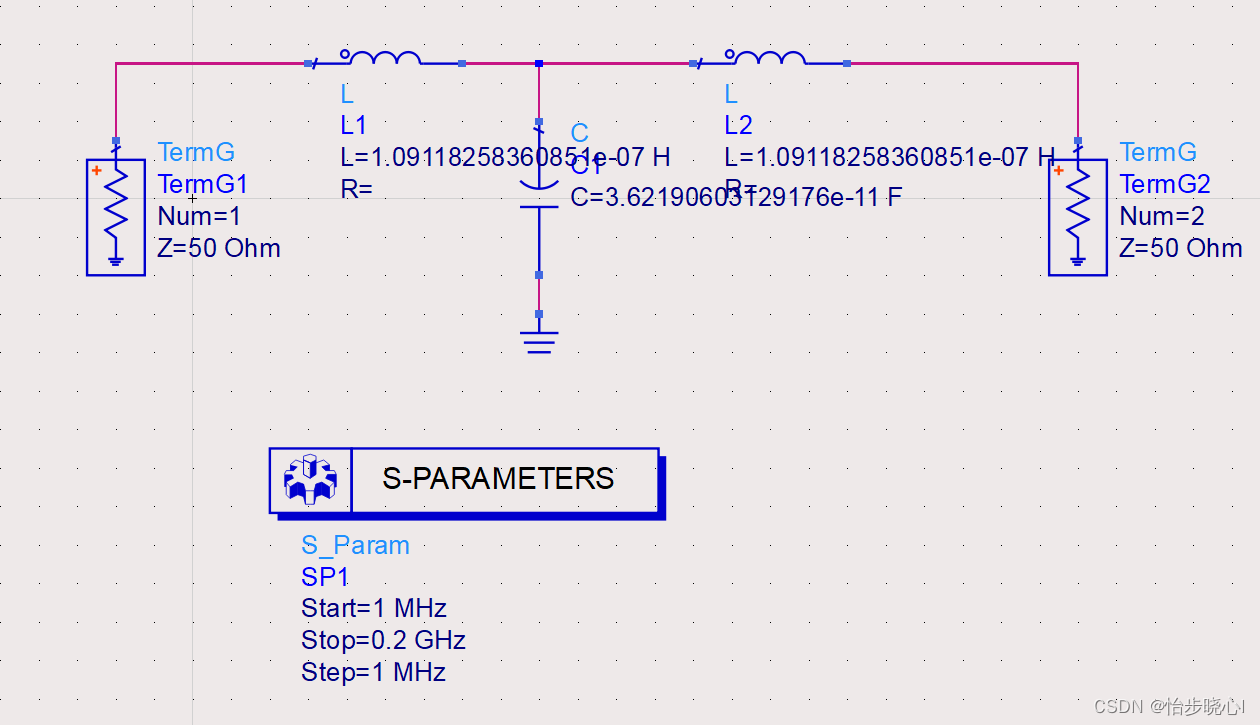
此处给出的是三阶的设计案例，得到的结果如下所示：

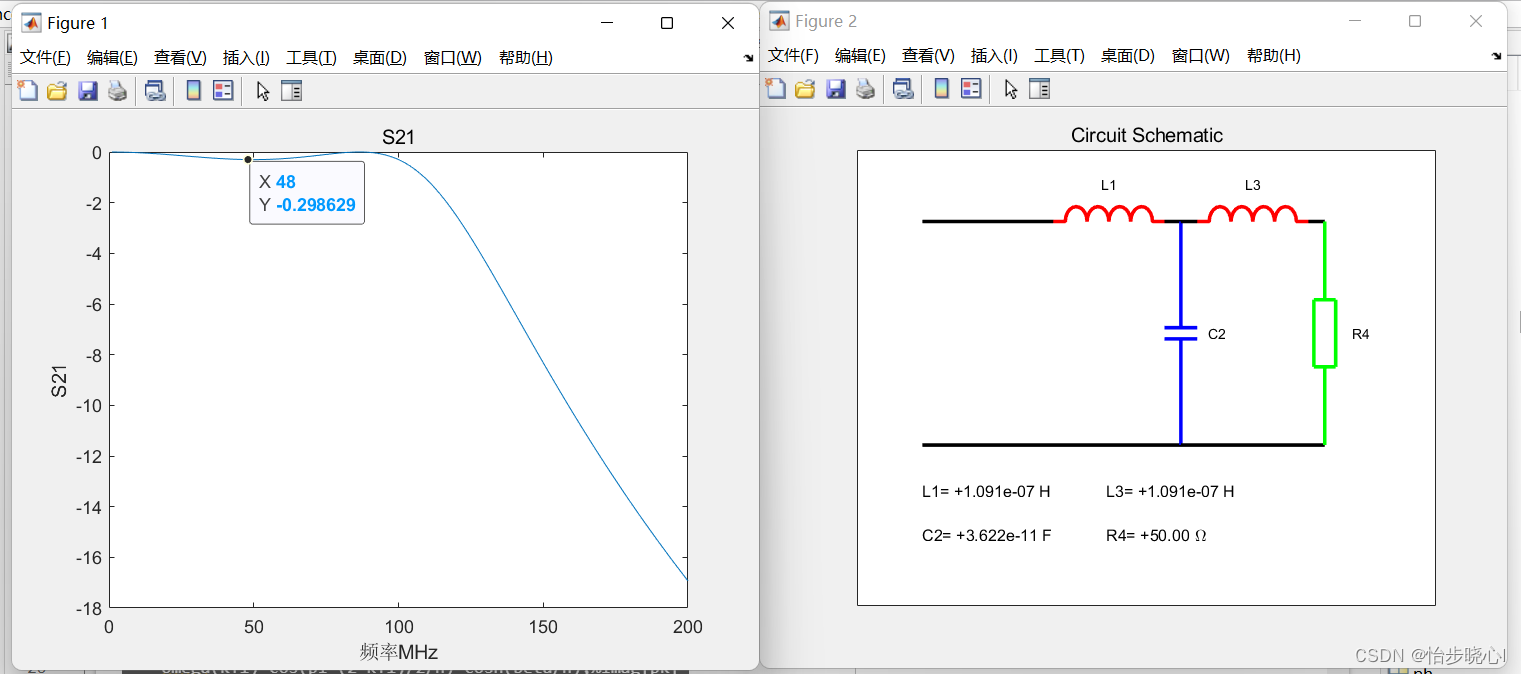
2、ADS进行验证

ADS进行验证：

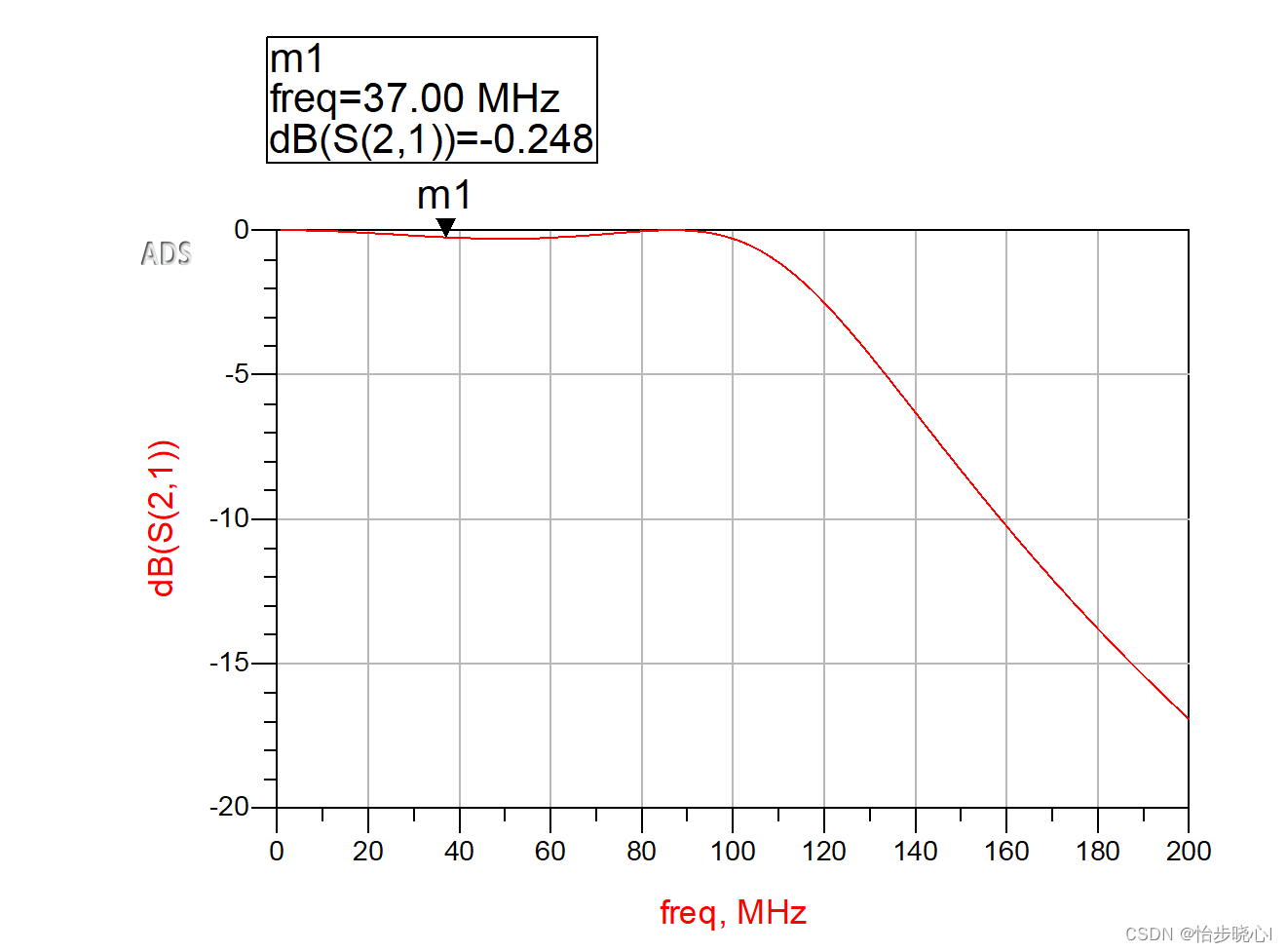
3、更多案例

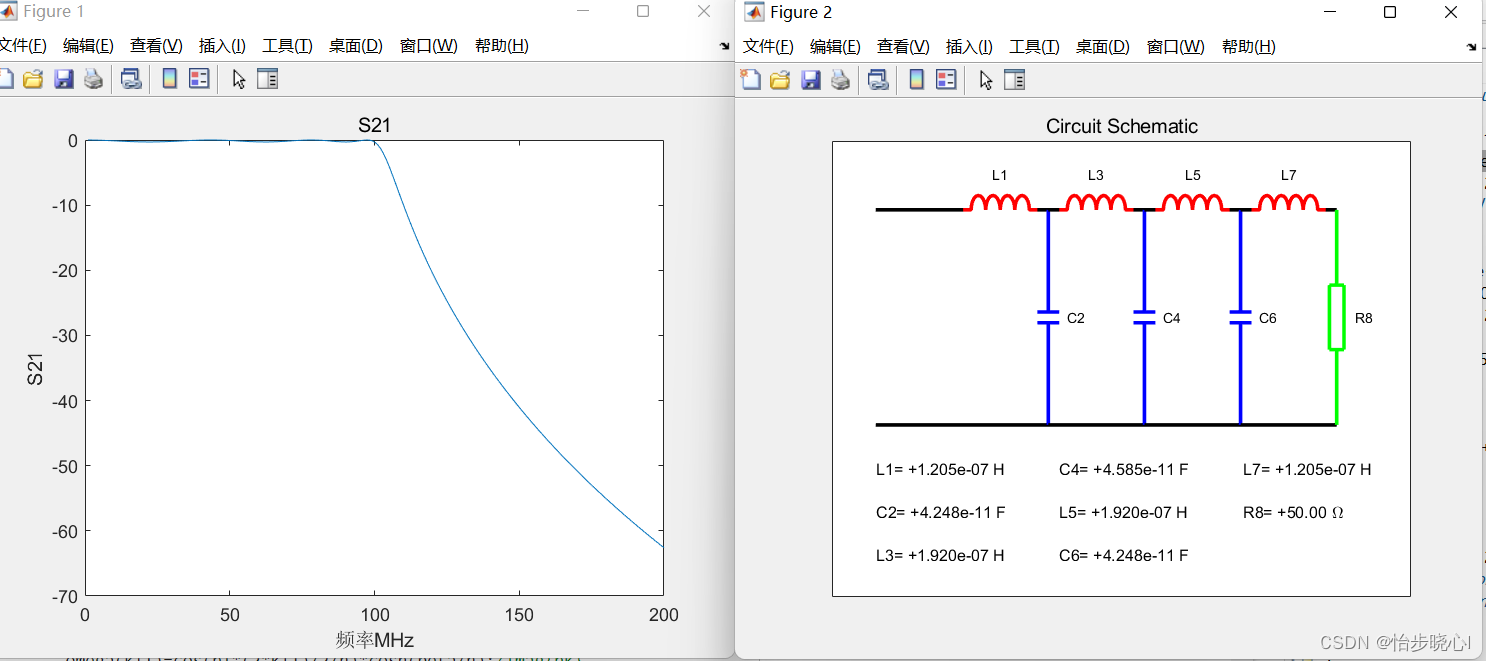
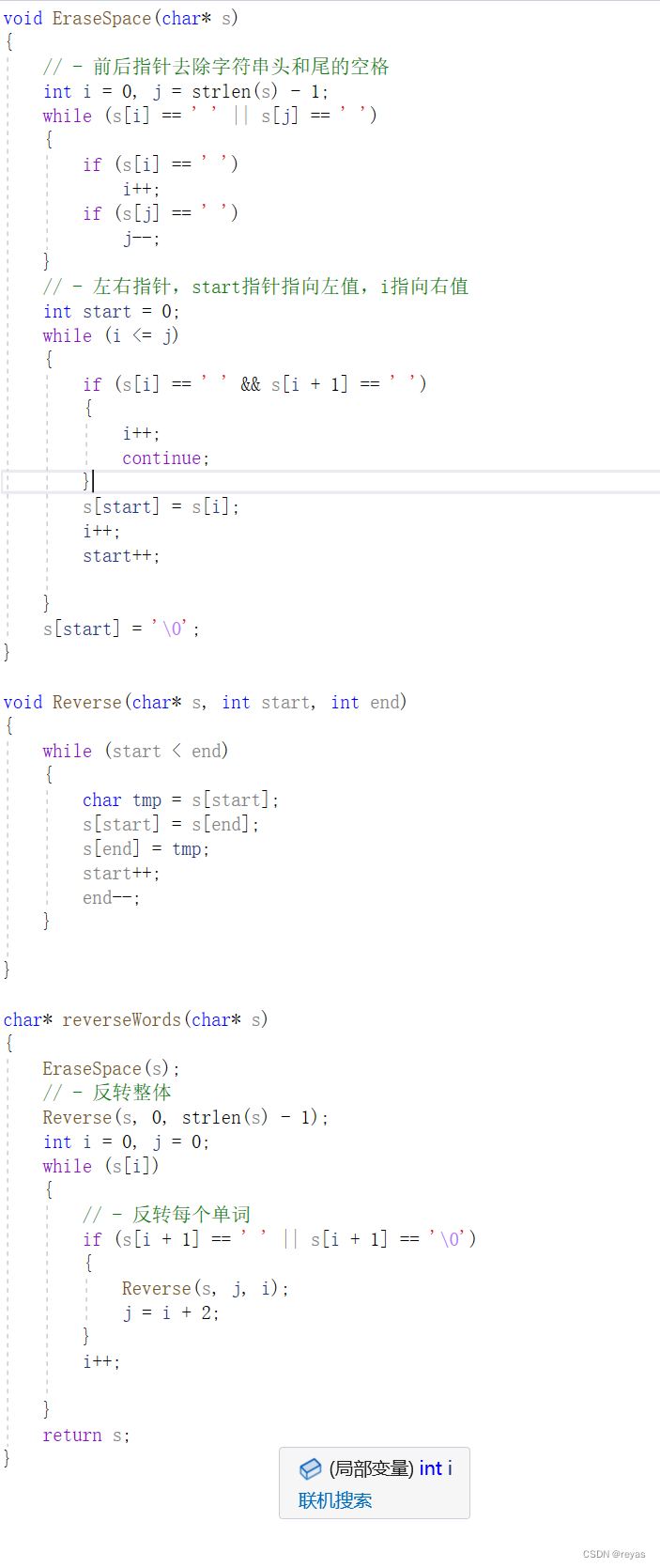
当然，也可以设计7阶数的，简单修改一下参数即可：