红黑树，AVLTree树底层实现逻辑都是平衡二叉树（AVLTree高度平衡，红黑树以某种规则平衡），但终究不像链表的迭代器那样逻辑简单。

        简单叙述以下，二叉树上面迭代器的运行逻辑，根据下面的图，迭代器的begin就是二叉树的最左节点，end是二叉树根节点的父节点（NULL）。

        为什么要这样设计，因为平衡二叉树在中序遍历下是升序排列，所以只有首部begin在二叉树最左节点，向后++遍历时，才能打印有序数据。

        但是为什么end在根节点的父亲？

        因为外部循环while(it!=end()),是不等于end节点，所以在遍历完右子树后就像上返回找类似于下图中绿色的parent节点了(右子树遍历完向上找)，所以遍历完整颗二叉树后，就会向上找节点，到了父节点的父亲时就为空了，也就是end节点，所以就停止遍历了。

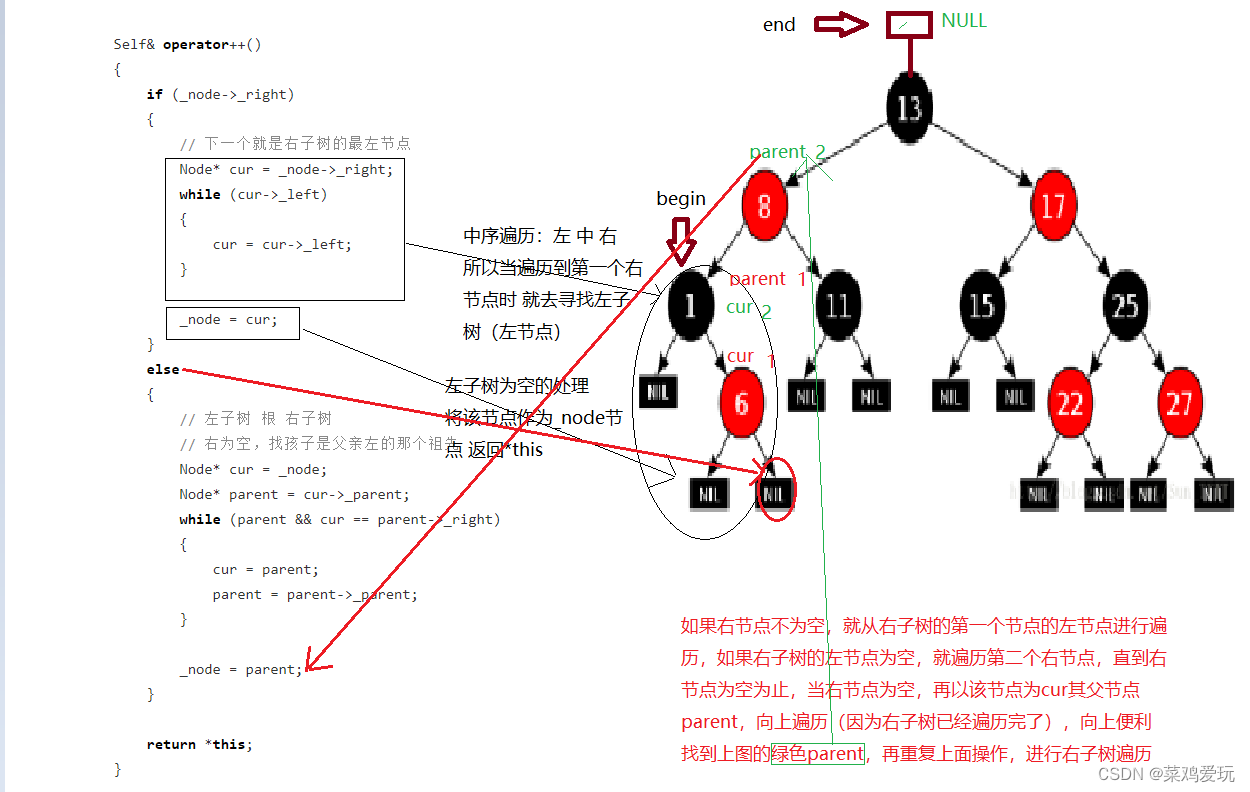
代码：

template<class T>
struct __TreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef __TreeIterator<T> Self;
	Node* _node;//迭代器存的是二叉树的节点

	__TreeIterator(Node* node)
		:_node(node)
	{}

	T& operator*()
	{
		return _node->_data;
	}

	T* operator->()
	{
		return &_node->_data;
	}
    //这就是平衡二叉树迭代器的运行核心 一定要理解这部分逻辑才能理解好这个迭代器
	Self& operator++()
	{
		if (_node->_right)
		{
			// 下一个就是右子树的最左节点
			Node* cur = _node->_right;
			while (cur->_left)
			{
				cur = cur->_left;
			}

			_node = cur;
		}
		else
		{
			// 左子树 根 右子树
			// 右为空，找孩子是父亲左的那个祖先
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_right)
			{
				cur = parent;
				parent = parent->_parent;
			}

			_node = parent;
		}

		return *this;
	}

    //给外界判断提供的
	bool operator!=(const Self& s)
	{
		return _node != s._node;
	}

	bool operator==(const Self& s)
	{
		return _node == s._node;
	}
};

	Self& operator--()
	{
		if (_node->_left)
		{
			Node* subRight = _node->_left;
			while (subRight->_right)
			{
				subRight = subRight->_right;
			}

			_node = subRight;
		}
		else
		{
			// 孩子是父亲的右的那个节点
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_left)
			{
				cur = cur->_parent;
				parent = parent->_parent;
			}

			_node = parent;
		}

		return *this;
	}