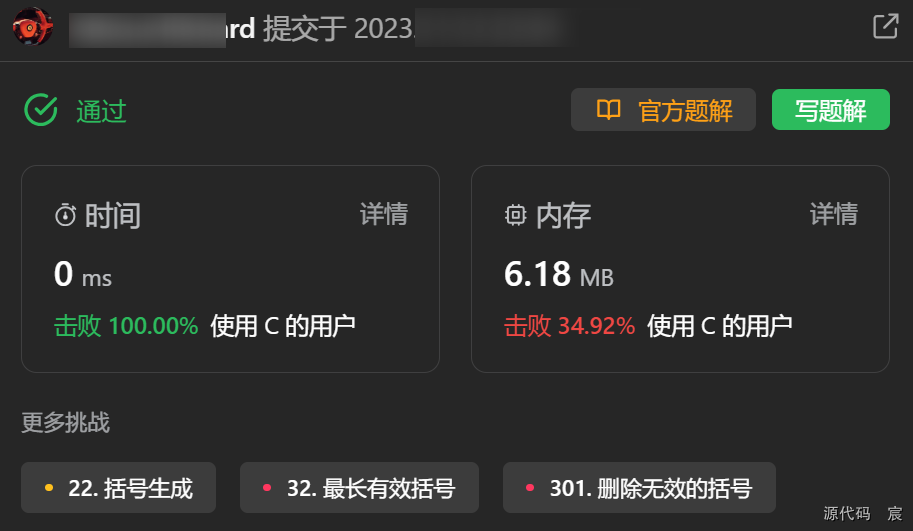
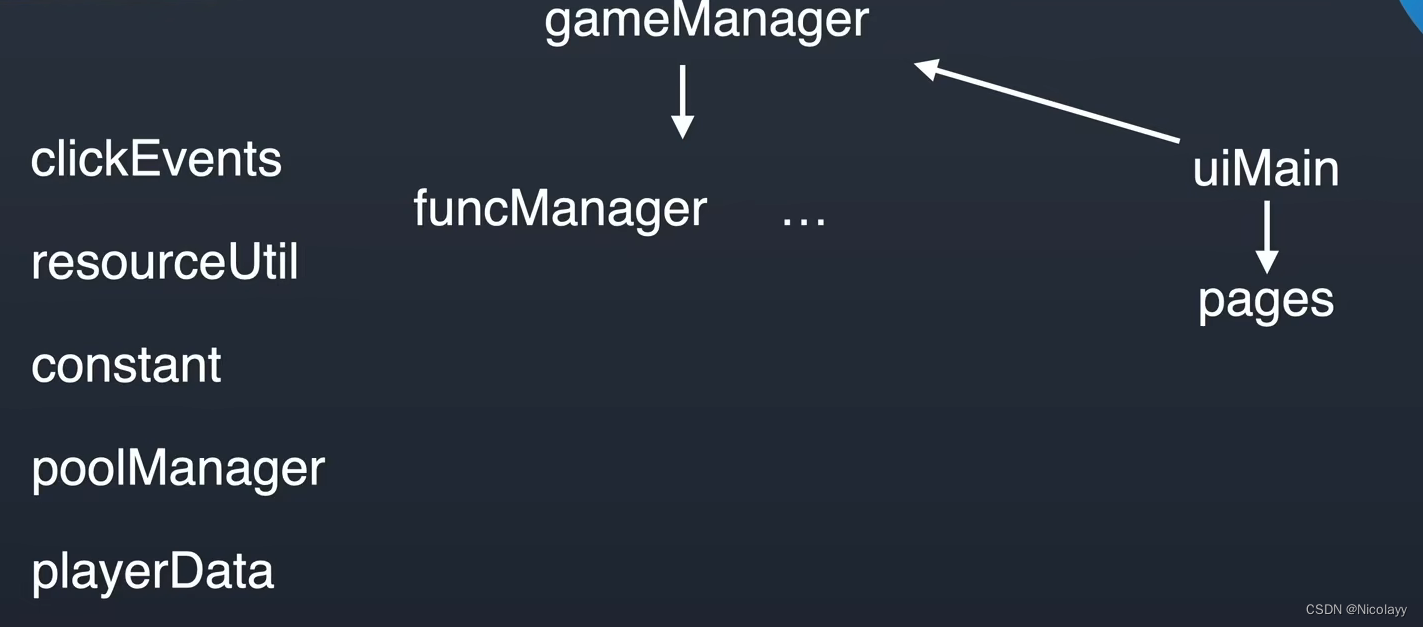
P3842 [TJOI2007] 线段
时间:2023.11.7
题目地址:[TJOI2007] 线段
题目分析
这题就是练一下动态规划的。
首先确定dp数组:
d
p
[
i
]
[
0
/
1
]
dp[i][0/1]
dp[i][0/1],
i
i
i代表第几行,然后每行
d
p
[
i
]
[
0
]
dp[i][0]
dp[i][0]代表的就是每次走完这一行线段后停在
l
e
f
t
left
left的最短距离;每行
d
p
[
i
]
[
1
]
dp[i][1]
dp[i][1]代表的就是每次走完这一行线段后停在
r
i
g
h
t
right
right的最短距离。
只有可能是停在这一行的两个位置左端点或者右端点,其余点不可能会满足最小的。
然后,就是状态转移方程了。
d
p
[
i
]
[
0
]
=
m
i
n
(
d
p
[
i
−
1
]
[
0
]
+
a
b
s
(
a
[
i
]
[
1
]
−
a
[
i
−
1
]
[
0
]
)
,
d
p
[
i
]
[
1
]
+
a
b
s
(
a
[
i
]
[
1
]
−
a
[
i
−
1
]
[
1
]
)
)
+
l
e
n
(
i
)
+
1
dp[i][0] = min(dp[i-1][0] + abs(a[i][1] - a[i-1][0]), dp[i][1] + abs(a[i][1]-a[i-1][1])) + len(i) + 1
dp[i][0]=min(dp[i−1][0]+abs(a[i][1]−a[i−1][0]),dp[i][1]+abs(a[i][1]−a[i−1][1]))+len(i)+1
d
p
[
i
]
[
0
]
=
m
i
n
(
d
p
[
i
−
1
]
[
0
]
+
a
b
s
(
a
[
i
]
[
0
]
−
a
[
i
−
1
]
[
0
]
)
,
d
p
[
i
]
[
1
]
+
a
b
s
(
a
[
i
]
[
0
]
−
a
[
i
−
1
]
[
1
]
)
)
+
l
e
n
(
i
)
+
1
dp[i][0] = min(dp[i-1][0] + abs(a[i][0] - a[i-1][0]), dp[i][1] + abs(a[i][0]-a[i-1][1])) + len(i) + 1
dp[i][0]=min(dp[i−1][0]+abs(a[i][0]−a[i−1][0]),dp[i][1]+abs(a[i][0]−a[i−1][1]))+len(i)+1
直接看肯定是有点抽象,建议直观画图来理解。
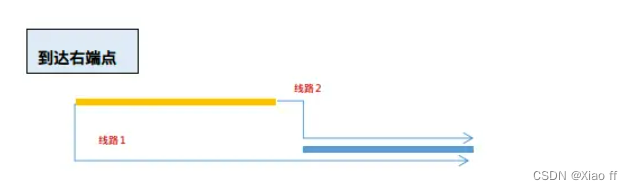
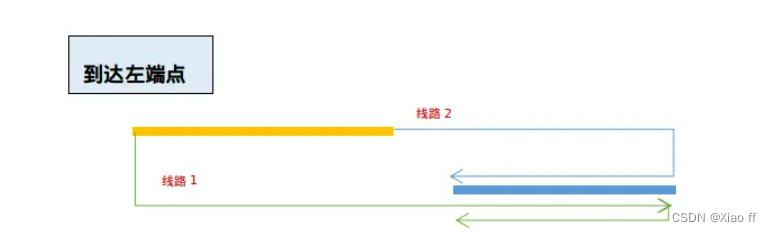
还有其他几种位置不同的但加上绝对值后,其实发现就是一样的,跟位置没什么关系,找到点与点之间的距离是多走的就行了。
最后是要到
n
n
n所以还有简单的加上最后一段路就行了。

代码
n = int(input())
a = [[0, 0] for _ in range(n+1)] # 存第i行的左右端点
for i in range(n):
l, r = map(int, input().split())
a[i+1][0] = l
a[i+1][1] = r
dp = [[0, 0] for _ in range(n+1)]
# 初始化,理解不了就画图看一下关系就行了
dp[1][0] = 2*a[1][1] - a[1][0] - 1
dp[1][1] = a[1][1] - 1
for i in range(2, n+1):
dp[i][0] = min(dp[i-1][0] + a[i][1]-a[i][0] + abs(a[i][1]-a[i-1][0]), dp[i-1][1] + a[i][1]-a[i][0] + abs(a[i][1]-a[i-1][1]))+1
dp[i][1] = min(dp[i-1][0] + a[i][1]-a[i][0] + abs(a[i][0]-a[i-1][0]), dp[i-1][1] + a[i][1]-a[i][0] + abs(a[i][0]-a[i-1][1]))+1
# 最终到达n
print(min(dp[n][0] + n - a[n][0], dp[n][1] + n - a[n][1]))