今天读的是一篇发表在ICCV 2023上的文章,作者来自华中科技大学。
文章地址:点击前往
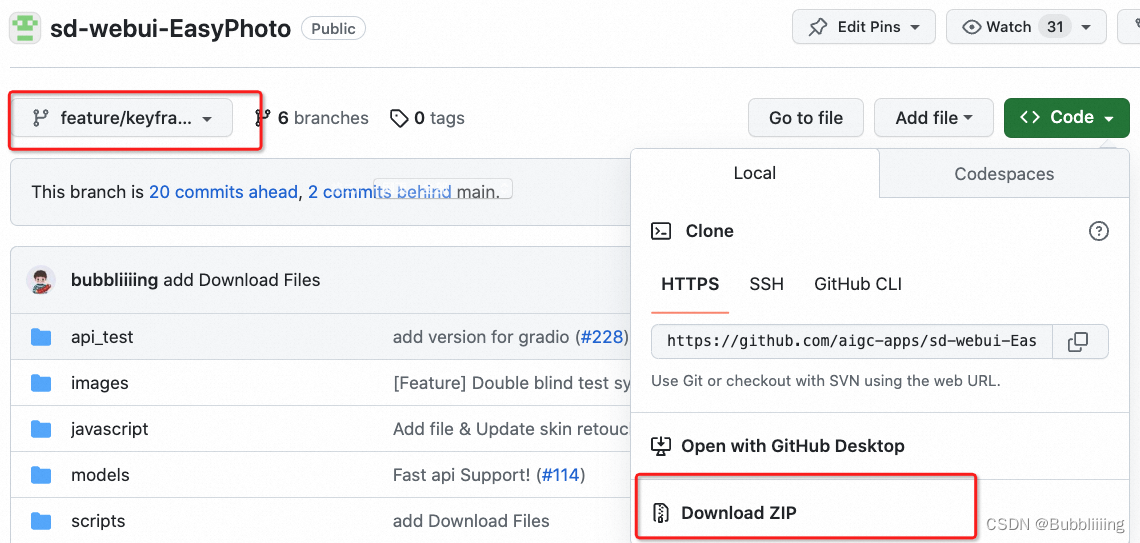
项目地址:Github
文章目录
- Abstract
- 1 Introduction
- 2 Relative Work
- 3 Motivation
- 3.1 Estimated bias and interpolated bias
- 3.2 One-sided V.S. Saddle-shaped
- 4 Dual-Depth Prediction
- 4.1 Review of learning-based MVS
- 4.2 Dual-Depth
- 4.3 Cascade Dual-Depths
- 4.4 DMVSNet
- 5 Experiments
- 6 Ablation Study
- 7 Conclusion
Abstract
现有方法忽略了一个事实,即合适的深度几何形状在 MVS 中也至关重要。 在本文中,我们证明了即使使用相同的深度预测误差,不同的深度几何形状也具有显着的性能差距。 因此,我们引入了由鞍形细胞组成的理想深度几何形状,其预测深度图围绕真实表面向上和向下振荡,而不是保持连续且平滑的深度平面。 为了实现这一目标,我们开发了一个名为 Dual-MVSNet (DMVSNet) 的从粗到细的框架,它可以产生一个振荡的深度平面。 从技术上讲,我们预测每个像素的两个深度值(双深度),并提出一种新颖的损失函数和棋盘形选择策略来约束预测的深度几何形状。 与现有方法相比,DMVSNet在DTU基准测试中取得了较高的排名,并在Tanks and Temples等具有挑战性的场景中获得了顶尖的性能,展示了其强大的性能和泛化能力。 我们的方法还指出了在MVS中考虑深度几何的新研究方向。
1 Introduction
在这项工作中,我们引入了在 MVS 中考虑深度几何的新视角。 我们首次提出了鞍形单元的深度几何结构,并证明了其对于 MVS 重建任务的重要性。 技术上,我们提出了双深度方法来实现鞍形单元,并设计了相应的网络框架DMVSNet。 借助双深度方法,DMVSNet 在 DTU 数据集上实现了顶级性能,在 Tanks 和 Temple 数据集上实现了 SOTA 性能。
2 Relative Work
介绍了传统和基于学习的MVS。
3 Motivation
3.1 Estimated bias and interpolated bias

在图2所示的fusion过程中,参考视图中的像素使用估计的深度图投影到空间中的 3D 点上。 然后使用各自的相机参数将该 3D 点重新投影到其他视图中的子像素上,并使用相应的深度图来获取新的 3D 点。 最终的 3D 重建结果由参考视图中像素的深度差和其他视图中子像素的估计深度(例如,通过平均)确定。 因此,3D重建结果的准确性不仅受到估计深度图的准确性的影响,而且还受到子像素插值深度的准确性的影响。 子像素深度是通过线性插值相邻像素的深度来估计的,其准确性受到估计偏差和深度单元†的影响。 图4显示,在相同的估计偏差和插值位置下,由于不同的深度单元,插值深度的精度会有所不同。 因此,考虑不同单元的深度几何形状对 MVS 的影响非常重要。

3.2 One-sided V.S. Saddle-shaped

为了简要说明深度单元的差异,我们在图3中提出了两个假设的深度单元: a)One-sided; b) Saddle-shaped。 我们假设具有相同绝对估计偏差“1”的插值位置是均匀分布的。 深度平面(黄色)和GT平面(蓝色)之间的spatial volume可以被视为预期的absolute interpolation error。 从数学上讲,““one-sided cell”的预期绝对插值误差是“saddle-shaped cell”的4倍。
为了定量证明不同单元的深度几何形状对 3D 点重建性能的影响,我们进行了验证实验。 在每个像素的绝对估计偏差相同的假设下,我们使用真实深度翻转估计的深度值,使它们按照图3所示的两个单元分布。表1中的实验结果表明,depth geometries with different cells对 3D 点重建的质量有显着影响,包括准确性和完整性,即使准确性差异超过 60%(表 1 中的第二行和第三行)。 这表明鞍形单元的深度几何结构是提高 MVS 性能的可行方法。


现有的大多数MVS方法都没有对深度单元施加约束,因此它们的深度图分布在由单边单元和鞍形单元组成的几何图形之间,这决定了3D点重建的精度介于由两种理想几何图形组成的性能之间 奇异细胞(如表1第一行所示)。 此外,在没有深度单元限制的情况下,尽管深度预测性能更好,但可能会获得较差的 3D 度量(表 2)。 我们如何约束网络生成具有更多鞍形单元的深度图? 在上面的实验中,使用groundtruth翻转估计深度的方法是一个先有鸡还是先有蛋的问题,在实际推理中是不可行的。 在下一节中,我们将引入双深度预测来解决这个困境。
4 Dual-Depth Prediction
4.1 Review of learning-based MVS
4.2 Dual-Depth
针对具有更多鞍形单元的振荡深度几何形状,我们选择预测每个像素的两个深度值。 如果双深度分布在真实深度的任一侧,启发式选择策略可以实现目标几何形状。
具体来说,我们为每个像素生成两个概率分布,并使用它们生成两个相应的深度D(参见等式(3))。 为了确保独立预测的双深度的准确性,我们采用 L1 损失来监督它们的预测值,如之前的工作一样。 直观上,如果不增加对偶深度联合分布的约束,得到的预测分布是无序的。 因此,我们提出了另一种新颖的损失来限制两个深度在地面实况周围对称分布:

其中
∣
⋅
∣
|·|
∣⋅∣表示绝对距离,
m
a
x
(
⋅
)
max(·)
max(⋅)和
m
i
n
(
⋅
)
min(·)
min(⋅)取沿第一维的最大值和最小值,例如
m
a
x
(
D
)
=
m
a
x
(
D
[
1
,
:
,
:
]
,
D
[
2
,
:
,
:
]
)
max (D) = max (D[1, :, :], D[2, :, :])
max(D)=max(D[1,:,:],D[2,:,:])。
L
i
n
t
L_{int}
Lint 鼓励估计偏差不大于
∣
m
a
x
(
D
)
−
m
i
n
(
D
)
∣
|max(D) − min(D)|
∣max(D)−min(D)∣,使得间隔随着估计偏差的增加而增加,这保证了双深度分布在真实深度的两侧。 如果
m
a
x
(
D
)
=
m
i
n
(
D
)
=
D
g
max(D) = min(D) = D_{g}
max(D)=min(D)=Dg,
L
i
n
t
L_{int}
Lint 达到最小值,表明深度估计是无偏的,与
L
e
s
t
L_{est}
Lest 的目标一致。
当真实深度值位于预测的双深度之间时,我们提出一种棋盘选择策略来为每个像素选择合适的深度预测值。 具体来说,我们交替选择最大和最小预测深度值,创建类似于棋盘的分布。 如图5(a)所示,像素(x,y)的深度由下式确定:

它生成振荡深度图
D
c
D_{c}
Dc 。 如图6所示,通过双深度方法获得的深度图实现了由鞍形单元组成的几何形状。 框内的深度图是平滑的,表明预测值接近真实值。 同时,其对应的深度几何形状呈现出马鞍形的形态,这与我们的预期是一致的。


然而,当
(
x
,
y
)
(x,y)
(x,y)处的真实深度值不在
m
i
n
(
D
)
(
x
,
y
)
min(D)(x,y)
min(D)(x,y)和
m
a
x
(
D
)
(
x
,
y
)
max(D)(x,y)
max(D)(x,y)范围内时,上述方法可能会带来增加深度预测误差的潜在风险 。 为了解决这个问题,我们建议使用Cascade Dual-Depths。
4.3 Cascade Dual-Depths
这里主要讲了怎么改进confidence map来适配dual depth。


4.4 DMVSNet

5 Experiments
实验结果还不错,但并不是文章所说的SOTA,发表的时候无论是同样中了ICCV 2023的ET-MVSNet(甚至作者同样也来自华科)还是之前CVPR 2023的GeoMVSNet都表现更好。