目录
一、数据集及分析对象
二、目的及分析任务
三、方法及工具
四、数据读入
五、数据理解
六、数据准备
七、模型训练
八、模型评价
九、模型调参
十、模型预测
实现回归分析类算法的Python第三方工具包比较常用的有statsmodels、statistics、scikit-learn等,下面我们主要采用statsmodels。
一、数据集及分析对象
CSV文件——“women.csv”。
数据集链接:https://download.csdn.net/download/m0_70452407/88519967
该数据集给出了年龄在30~39岁的15名女性的身高和体重数据,主要属性如下:
(1)height:身高
(2)weight:体重
二、目的及分析任务
理解机器学习方法在数据分析中的应用——采用简单线性回归、多项式回归方法进行回归分析。
(1)训练模型。
(2)对模型进行拟合优度评价和可视化处理,验证简单线性回归建模的有效性。
(3)采用多项式回归进行模型优化。
(4)按多项式回归模型预测体重数据。
三、方法及工具
Python语言及第三方工具包pandas、matplotlib和statsmodels。
四、数据读入
import pandas as pd
df_women=pd.read_csv("D:\\Download\\JDK\\数据分析理论与实践by朝乐门_机械工业出版社\\第3章 回归分析\\women.csv",
index_col=0)五、数据理解
对数据框df_women进行探索性分析。
df_women.describe()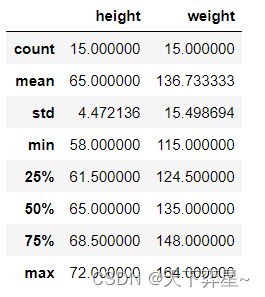
df_women.shape(15, 2)
接着,对数据库df_women进行数据可视化分析,通过调用mayplotlib.pyplot包中数据框(DataFrame)的scatter()方法绘制散点图。
import matplotlib.pyplot as plt
plt.scatter(df_women["height"],df_women["weight"])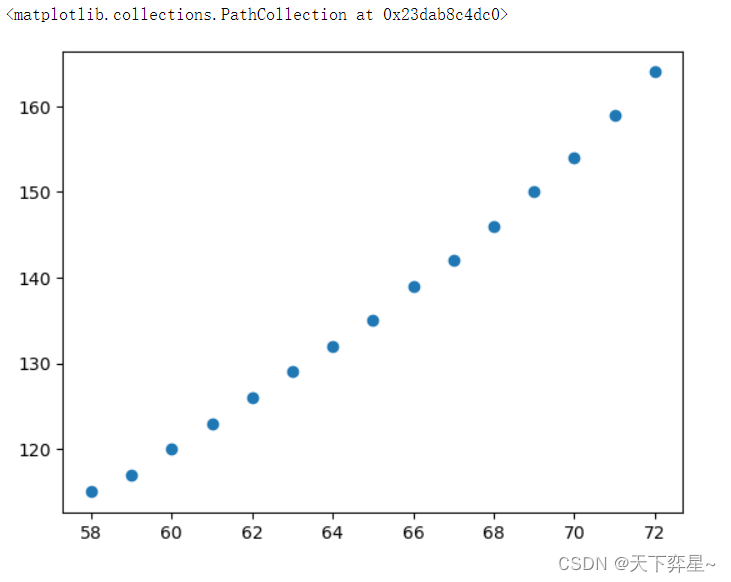
从输出结果可以看出,女性身高与体重之间的关系可以进行线性回归分析,需要进一步进行数据准备工作。
六、数据准备
进行线性回归分析之前,应准备好模型所需的特征矩阵(X)和目标向量(y)。这里我们采用Python的统计分析包statsmodel进行自动类型转换。
X=df_women['height']
y=df_women['weight']七、模型训练
以女性身高height作为自变量、体重weight作为因变量对数据进行简单线性回归建模,这里采用Python的统计分析包statsmodels中的OLS函数进行建模分析。
import statsmodels.api as smstatsmodels.OLS()方法的输入有(endog,exog,missing,hasconst)4个,其中,endog是回归中的因变量,即上述模型中的weight,exog则是自变量的值,即模型中的height。
默认情况下,statsmodels.OLS()方法不含截距项,因此应将模型中的常数项看作基为1的维度上的系数。所以,exog的输入中,最左侧的一列的数值应全为1。这里我们采用statsmodels中提供的可直接解决这一问题的方法——sm.add_constant()给X新增一列,列名为const,每行取值为1.0
X_add_const=sm.add_constant(X)
X_add_const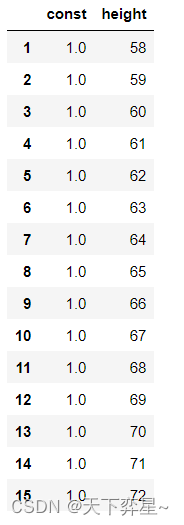
在自变量X_add_const和因变量y上使用OLS()方法进行简单线性回归。
myModel=sm.OLS(y,X_add_const)然后获取拟合结果,并调用summary()方法显示回归拟合的结果。
results=myModel.fit()
print(results.summary())OLS Regression Results ============================================================================== Dep. Variable: weight R-squared: 0.991 Model: OLS Adj. R-squared: 0.990 Method: Least Squares F-statistic: 1433. Date: Thu, 09 Nov 2023 Prob (F-statistic): 1.09e-14 Time: 18:28:09 Log-Likelihood: -26.541 No. Observations: 15 AIC: 57.08 Df Residuals: 13 BIC: 58.50 Df Model: 1 Covariance Type: nonrobust ============================================================================== coef std err t P>|t| [0.025 0.975] ------------------------------------------------------------------------------ const -87.5167 5.937 -14.741 0.000 -100.343 -74.691 height 3.4500 0.091 37.855 0.000 3.253 3.647 ============================================================================== Omnibus: 2.396 Durbin-Watson: 0.315 Prob(Omnibus): 0.302 Jarque-Bera (JB): 1.660 Skew: 0.789 Prob(JB): 0.436 Kurtosis: 2.596 Cond. No. 982. ============================================================================== Notes: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. C:\ProgramData\Anaconda3\lib\site-packages\scipy\stats\_stats_py.py:1769: UserWarning: kurtosistest only valid for n>=20 ... continuing anyway, n=15 warnings.warn("kurtosistest only valid for n>=20 ... continuing "
上述运行结果中第二部分的coef列所对应的const和height就是计算出的回归模型中的截距项和斜率。
除了读取回归摘要外,还可以调用params属性查看拟合结果的斜率和截距。
results.paramsconst -87.516667 height 3.450000 dtype: float64
从输出结果可以看出,回归模型中的截距项和斜率分别为-87.516667和3.450000
八、模型评价
以R^2(决定系数)作为衡量回归直线对观测值拟合程度的指标,其取值范围为[0,1],越接近1,说明“回归直线的拟合优度越好”。可以调用requared属性查看拟合结果的R^2
results.rsquared0.9910098326857505
除了决定系数等统计量,还可以通过可视化方法更直观地查看回归效果。这里我们调用matplotlib.pyplot包中的plot()方法,将回归直线与真实数据绘制在一个图中进行比较。
y_predict=results.params[0]+results.params[1]*df_women["height"]
plt.rcParams['font.family']="simHei" #汉字显示 字体设置
plt.plot(df_women["height"],df_women["weight"],"o")
plt.plot(df_women["height"],y_predict)
plt.title("女性身高与体重的线性回归分析")
plt.xlabel("身高")
plt.ylabel("体重")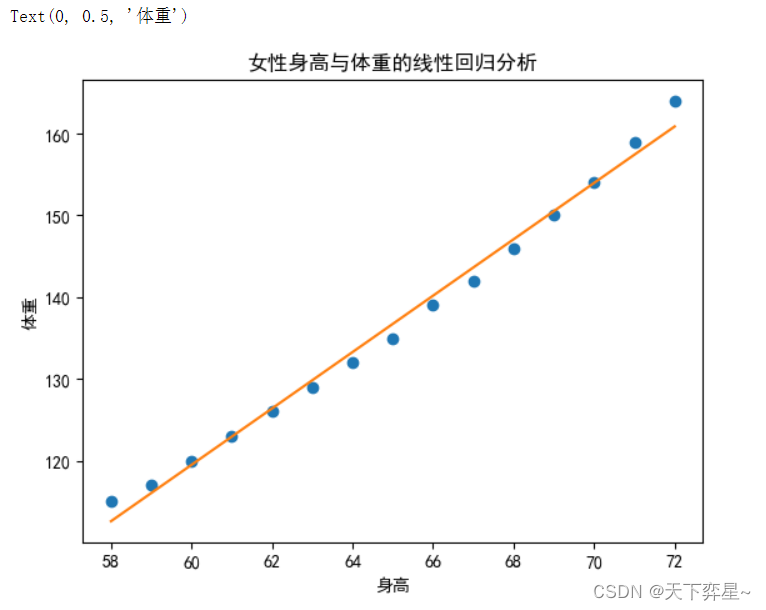
从输出结果可以看出,采用简单线性回归模型的效果还可以进一步优化,为此采取多项式回归方法进行回归分析。
九、模型调参
调用Python的统计分析包statsmodels中的OLS()方法对自变量女性身高height、因变量体重weight进行多项式回归建模。
假设因变量y与自变量X、X^2、X^3存在高元线性回归,因此在多项式分析中,特征矩阵由3部分组成,即X、X^2和X^3。通过调用numpy库的column_stack()方法创建特征矩阵X。
import numpy as np
X=np.column_stack((X,np.power(X,2),np.power(X,3)))通过sm.add_constant()方法保留多项式回归中的截距项。对自变量X_add_const和因变量y使用OLS()方法进行多项式回归。
X_add_const=sm.add_constant(X)
myModel_updated=sm.OLS(y,X_add_const)
results=myModel_updated.fit()
print(results.summary())OLS Regression Results ============================================================================== Dep. Variable: weight R-squared: 1.000 Model: OLS Adj. R-squared: 1.000 Method: Least Squares F-statistic: 1.679e+04 Date: Thu, 09 Nov 2023 Prob (F-statistic): 2.07e-20 Time: 18:46:54 Log-Likelihood: 1.3441 No. Observations: 15 AIC: 5.312 Df Residuals: 11 BIC: 8.144 Df Model: 3 Covariance Type: nonrobust ============================================================================== coef std err t P>|t| [0.025 0.975] ------------------------------------------------------------------------------ const -896.7476 294.575 -3.044 0.011 -1545.102 -248.393 x1 46.4108 13.655 3.399 0.006 16.356 76.466 x2 -0.7462 0.211 -3.544 0.005 -1.210 -0.283 x3 0.0043 0.001 3.940 0.002 0.002 0.007 ============================================================================== Omnibus: 0.028 Durbin-Watson: 2.388 Prob(Omnibus): 0.986 Jarque-Bera (JB): 0.127 Skew: 0.049 Prob(JB): 0.939 Kurtosis: 2.561 Cond. No. 1.25e+09 ============================================================================== Notes: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. [2] The condition number is large, 1.25e+09. This might indicate that there are strong multicollinearity or other numerical problems. C:\ProgramData\Anaconda3\lib\site-packages\scipy\stats\_stats_py.py:1769: UserWarning: kurtosistest only valid for n>=20 ... continuing anyway, n=15 warnings.warn("kurtosistest only valid for n>=20 ... continuing "
从输出结果可以看出,多项式回归模型中的截距项为-896.7476,而X、X^2、X^3对应的斜率分别为46.4108、-0.7462和0.0043
调用requared属性查看拟合结果的R^2:
results.rsquared0.9997816939979361
从决定系数的结果可以看出,多项式回归模型的效果比简单线性回归模型的效果更好。
十、模型预测
使用该多项式回归模型进行体重预测并输出预测结果。
y_predict_updated=results.predict()
y_predict_updatedarray([114.63856209, 117.40676937, 120.18801264, 123.00780722, 125.89166846, 128.86511168, 131.95365223, 135.18280543, 138.57808662, 142.16501113, 145.9690943 , 150.01585147, 154.33079796, 158.93944911, 163.86732026])
多项式回归模型的可视化:
y_predict=(results.params[0]+results.params[1]*df_women["height"]+
results.params[2]*df_women["height"]**2+
results.params[3]*df_women["height"]**3)
plt.plot(df_women["height"],df_women["weight"],"o")
plt.plot(df_women["height"],y_predict)
plt.title("女性身高与体重的多项式回归分析")
plt.xlabel("身高")
plt.ylabel("体重")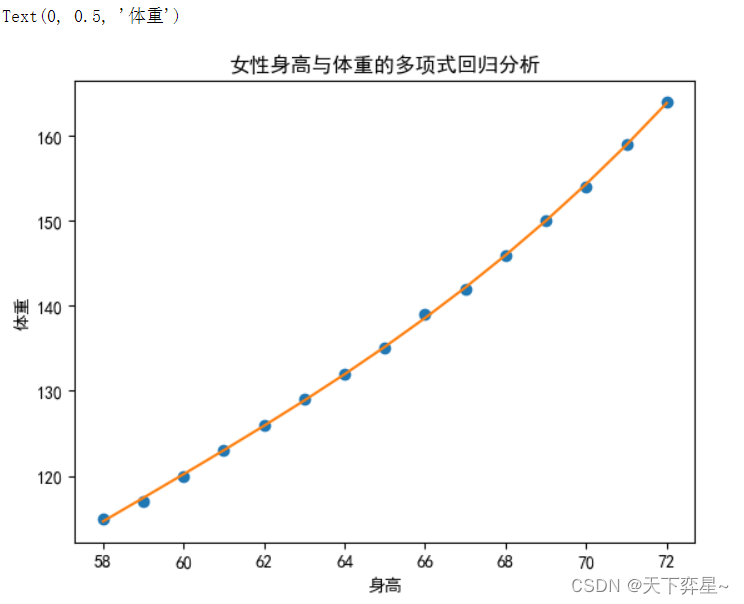
从结果可以看出,采用多项式回归后拟合效果显著提高,结果较为令人满意。