一、起源
训练深度网络的时候经常发生训练困难的问题,因为,每一次参数迭代更新后,上一层网络的输出数据经过这一层网络计算后,数据的分布会发生变化,为下一层网络的学习带来困难。
Batch Normalizatoin 之前的解决方案就是使用较小的学习率,和小心的初始化参数,对数据做白化处理,但是显然治标不治本。
Batch Normalization是在每个mini-batch进行归一化操作,并将归一化操作作为模型体系结构的一部分,使用BN可以获得如下的好处:

虽然随机梯度是简单有效的,但它需要仔细调整模型的超参数,特别是优化中使用的学习速率以及模型参数的初始值。训练的复杂性在于每层的输入受到前面所有层的参数的影响——因此当网络变得更深时,网络参数的微小变化就会被放大。如果我们能保证非线性输入的分布在网络训练时保持更稳定,那么优化器将不太可能陷入饱和状态,训练将加速。
二、BN层的作用
- 可以加快训练速率,即可以增大学习率,加快模型的收敛速度。
- 不过分依赖网络初始值。
- 一定程度上抑制了过拟合情况,降低了Dropout的必要性。
1.BN之前的一些减少Covariate Shift的方法
对网络的输入进行白化,网络训练将会收敛的更快——即输入线性变换为具有零均值和单位方差,并去相关。当每一层观察下面的层产生的输入时,实现每一层输入进行相同的白化将是有利的。通过白化每一层的输入,我们将采取措施实现输入的固定分布,消除Internal Covariate Shift的不良影响。那么如何消除呢?考虑在每个训练步骤或在某些间隔来白化激活值,通过直接修改网络或根据网络激活值来更改优化方法的参数,但这样会弱化梯度下降步骤。

通过白化操作,我们可以减缓ICS的问题,进而固定了每一层网络输入分布,加速网络训练过程的收敛。但是白话过程的计算成本太高,并且在每一轮训练中的每一层我们都需要做如此高成本计算的白化操作,这未免过于奢侈。而且白化过程由于改变了网络每一层的分布,因而改变了网络层中本身数据的表达能力,底层网络学习到的参数信息会被白化操作丢失掉。
2.BN算法描述
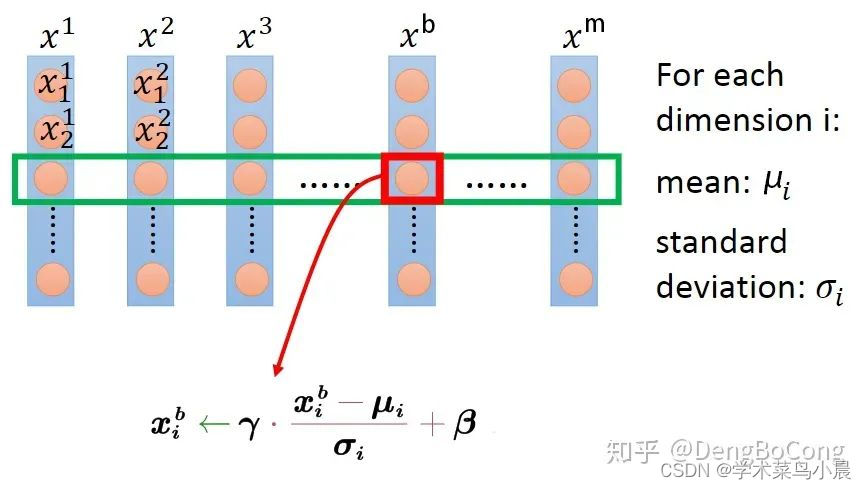
文中使用了类似z-score的归一化方式:每一维度减去自身均值,再除以自身标准差,由于使用的是随机梯度下降法,这些均值和方差也只能在当前迭代的batch中计算,故作者给这个算法命名为Batch Normalization。BN变换的算法如下所示,其中,为了数值稳定,e是一个加到小批量数据方差上的常量。




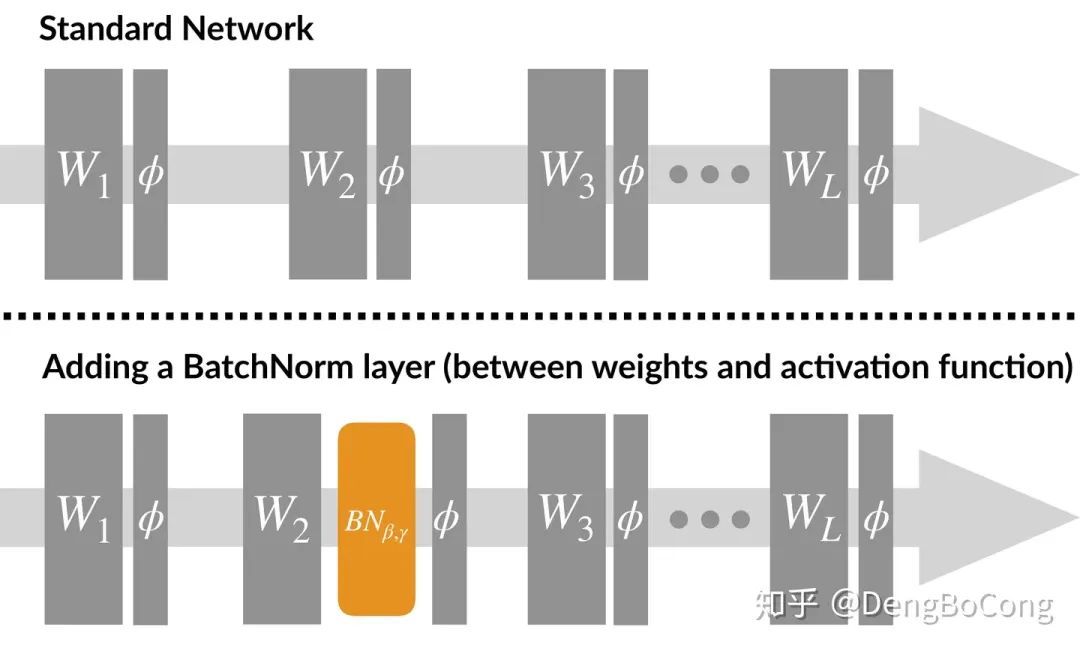
3.Batch Normalization的反向传播
讲反向传播之前,我们先来简单的写一下正向传递的代码,如下:

我们都知道,对于目前的神经网络计算框架,一个层要想加入到网络中,要保证其是可微的,即可以求梯度。BatchNorm的梯度该如何求取?反向传播求梯度只需抓住一个关键点,如果一个变量对另一个变量有影响,那么他们之间就存在偏导数,找到直接相关的变量,再配合链式法则,公式就很容易写出了。
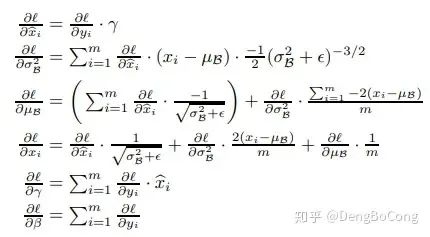

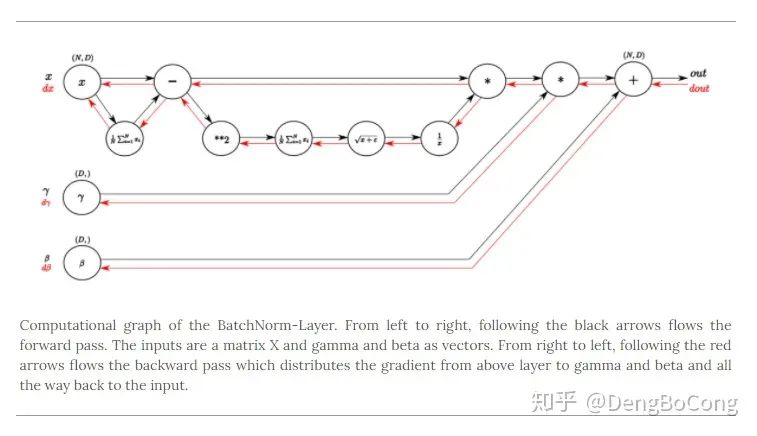
通过链式法则,我们可以对上面的正向传递的代码进行运算,得到反向传播的代码,如下(结合代码理解更方便):



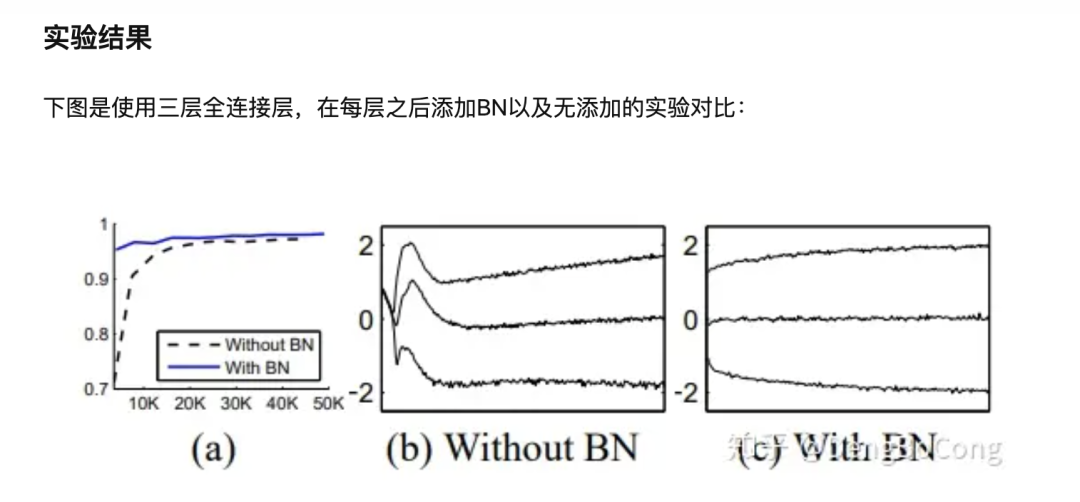
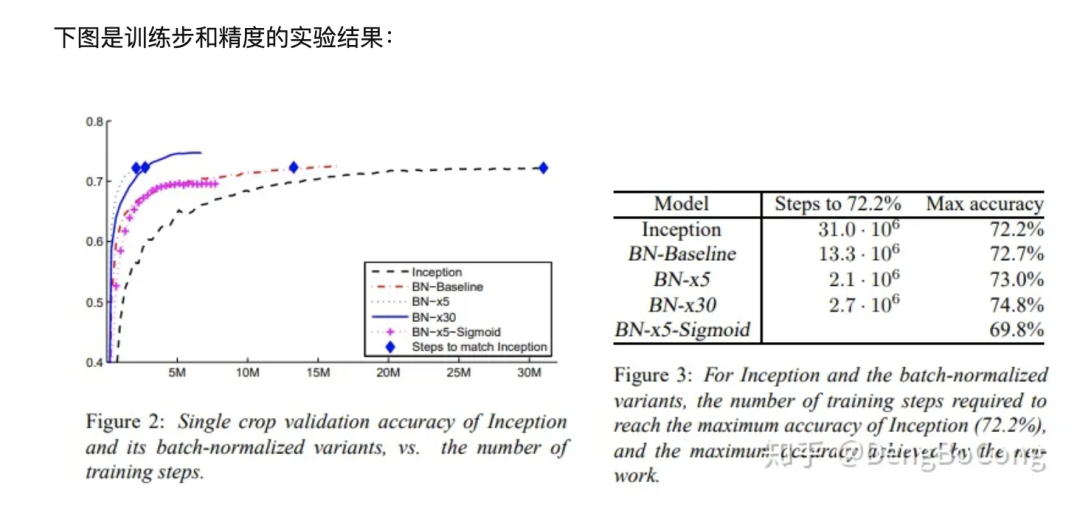
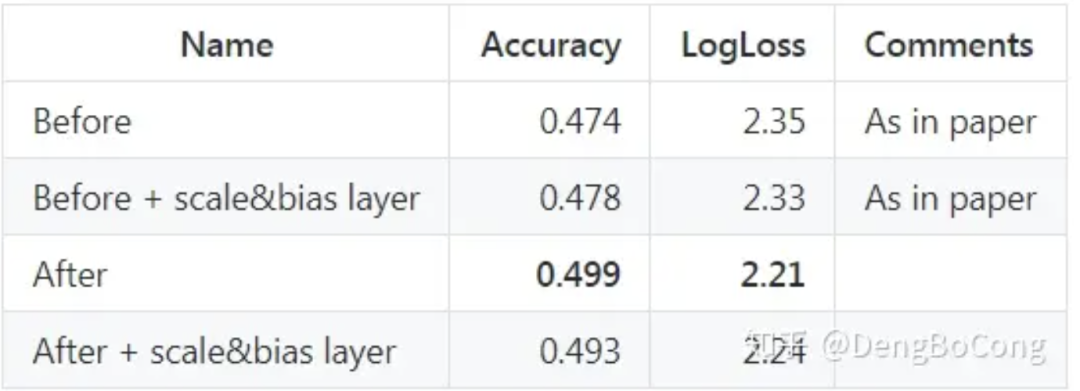
三、总结
Batch Normalization的加速作用体现在两个方面:一是归一化了每层和每维度的scale,所以可以整体使用一个较高的学习率,而不必像以前那样迁就小scale的维度;二是归一化后使得更多的权重分界面落在了数据中,降低了overfit的可能性,因此一些防止overfit但会降低速度的方法,例如dropout和权重衰减就可以不使用或者降低其权重。
BN层的有效性已有目共睹,但为什么有效可能还需要进一步研究,还需要进一步研究,这里整理了一些关于BN为什么有效的论文,贴在这:
How Does Batch Normalization Help Optimization?:
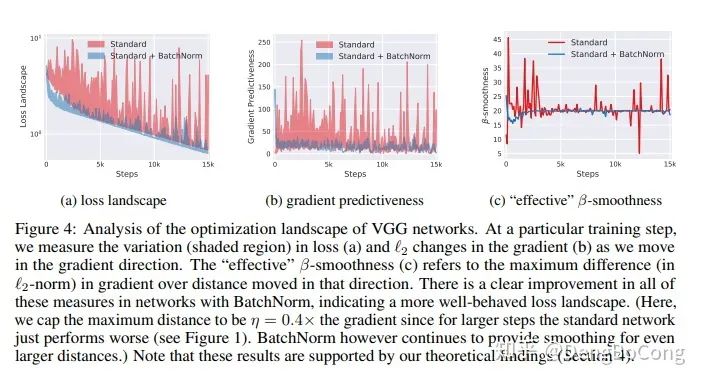
BN层让损失函数更平滑
https://arxiv.org/pdf/1805.11604.pdf
论文中通过分析训练过程中每步梯度方向上步长变化引起的损失变化范围、梯度幅值的变化范围、光滑度的变化,认为添加BN层后,损失函数的landscape(loss surface)变得更平滑,相比高低不平上下起伏的loss surface,平滑loss surface的梯度预测性更好,可以选取较大的步长。如下图所示: