文章目录
- Diffusion Model回顾
- Diffusion Model算法
- Training
- Inference
- 图像生成模型的本质目标
- MLE vs KL
- VAE
- DDPM
部分截图来自原课程视频《2023李宏毅最新生成式AI教程》,B站自行搜索。
Diffusion Model回顾
前情回顾[07.Diffusion Model概述](https://blog.csdn.net/oldmao_2001/article/details/1341964 78)
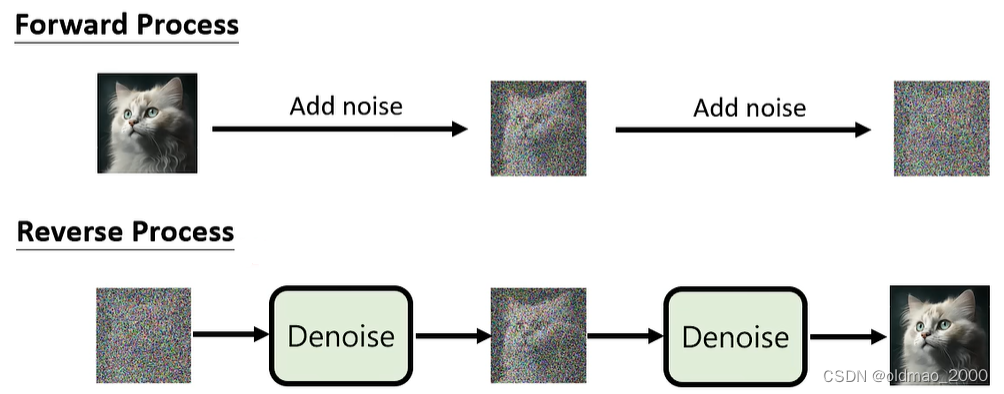
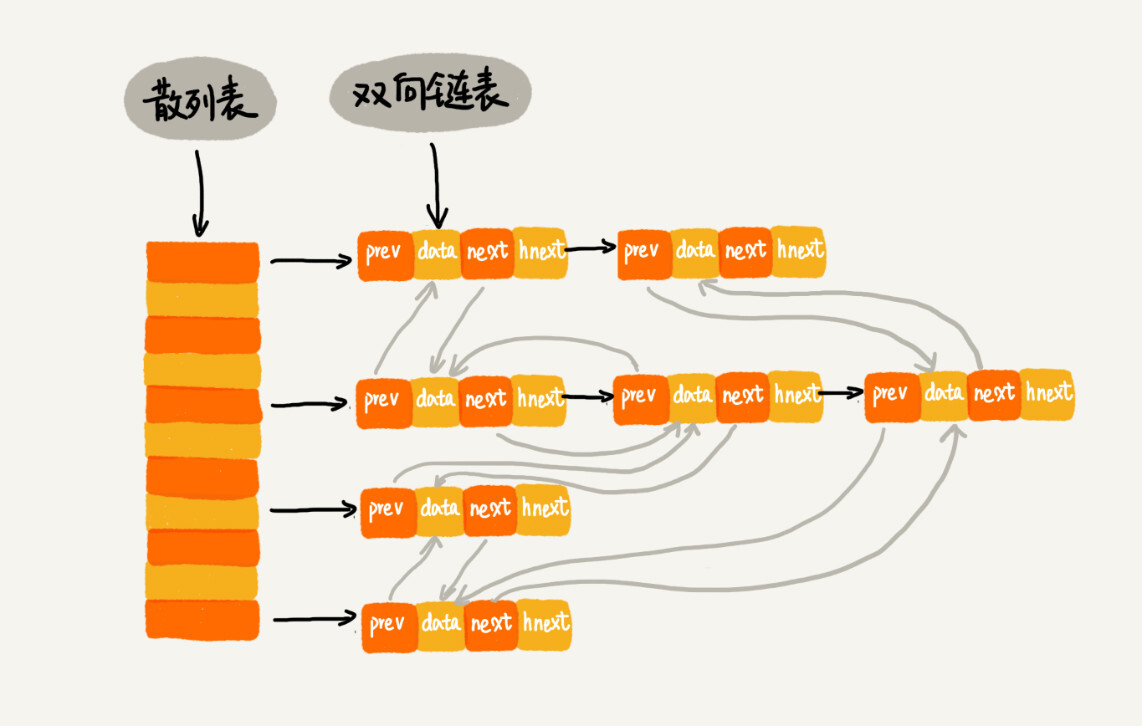
VAE和Diffusion Model在构架上比较相似:
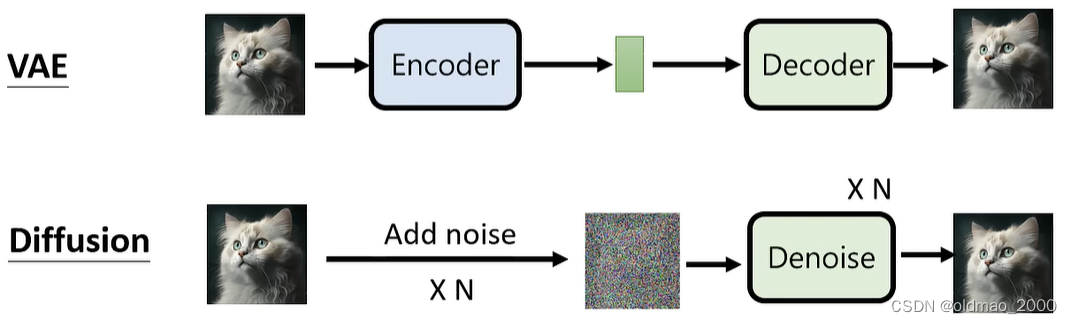
Diffusion Model算法
Training

第一行的repeat代表循环,执行2~5行,直到收敛停止。
第二行的
x
0
∼
q
(
x
0
)
x_0\sim q(x_0)
x0∼q(x0)中的
x
0
x_0
x0表示清晰的图片,整个语句表示采样一张图片。
第三行表示从
{
1
,
⋯
,
T
}
\{1,\cdots,T\}
{1,⋯,T}中采样一个整数
t
t
t,
T
T
T是一个很大的数字。
第四行表示从Normal Distribution中采样一个噪音
ϵ
\epsilon
ϵ

第五行比较复杂,先看:
α
ˉ
t
x
0
+
1
−
α
ˉ
t
ϵ
\sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\epsilon
αˉtx0+1−αˉtϵ
这里表示将清晰的图片与噪音按权重进行相加得到的结果:
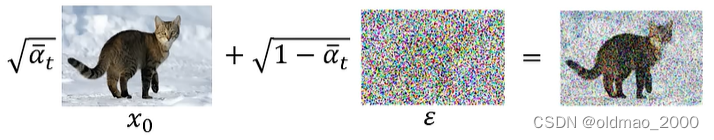
这里的权重:
α
ˉ
t
∈
→
s
m
a
l
l
e
r
{
α
ˉ
1
,
α
ˉ
2
,
⋯
,
α
ˉ
T
}
\bar{\alpha}_t \in \xrightarrow[smaller]{\{\bar{\alpha}_1,\bar{\alpha}_2,\cdots,\bar{\alpha}_T\}}
αˉt∈{αˉ1,αˉ2,⋯,αˉT}smaller
这里的
α
ˉ
1
\bar{\alpha}_1
αˉ1到
α
ˉ
T
\bar{\alpha}_T
αˉT是从大到小的关系。若从
T
T
T中采样到的
t
t
t越大,则
α
ˉ
t
\sqrt{\bar{\alpha}_t}
αˉt越小,
1
−
α
ˉ
t
\sqrt{1-\bar{\alpha}_t}
1−αˉt越大,表示二者相加时噪音占的权重就越大。
然后将权重相加结果丢进Noise predictor:
ϵ
θ
\epsilon_\theta
ϵθ
ϵ
θ
(
α
ˉ
t
x
0
+
1
−
α
ˉ
t
ϵ
,
t
)
\epsilon_\theta(\sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\epsilon,t)
ϵθ(αˉtx0+1−αˉtϵ,t)
然后计算预测结果与真实噪音的差异,并更新Noise predictor参数,使其预测结果越接近真实噪音越好。
需要注意的是,和上节课程中讲的有亿点点不一样,之前原理课中介绍Diffusion模型加噪音是逐步加的,在论文的具体实作上却是一步到位的,后面有推导为什么可以这样做:
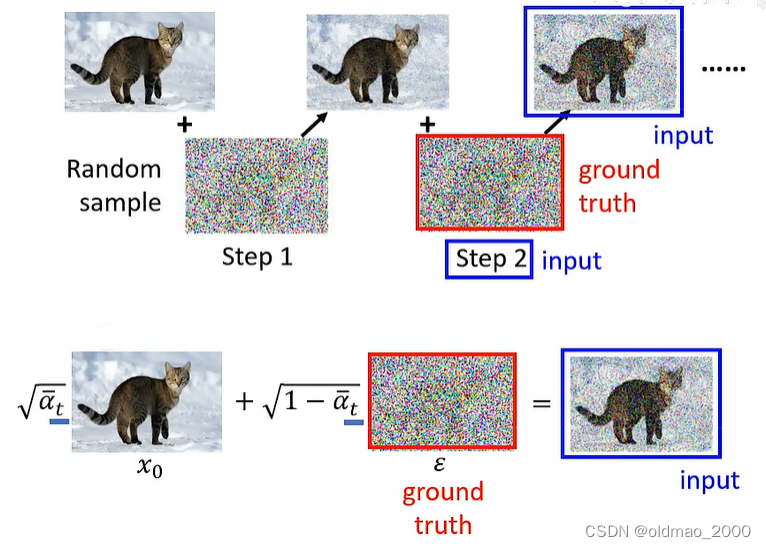
Inference

第一步,先从Normal Distribution中采样一个噪音
x
T
x_T
xT:

第二步,循环执行3,4步,共
T
T
T次
第三步,再从Normal Distribution中采样一个噪音
z
z
z
第四步中:
x
t
x_t
xt是第
t
t
t个步骤得到的结果:

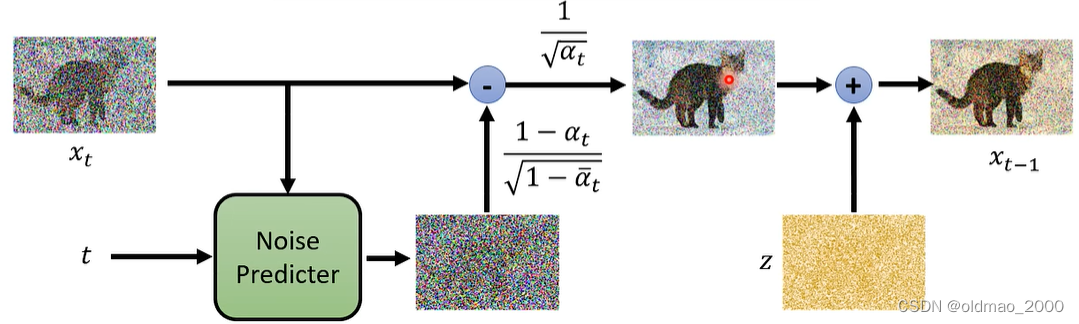
第四步
x
t
−
1
x_{t-1}
xt−1的公式可用下图表示,黄色部分忘记标上
δ
t
\delta_t
δt,此外还有两组权重:
{
α
ˉ
1
,
α
ˉ
2
,
⋯
,
α
ˉ
T
}
\{\bar{\alpha}_1,\bar{\alpha}_2,\cdots,\bar{\alpha}_T\}
{αˉ1,αˉ2,⋯,αˉT}和
{
α
1
,
α
2
,
⋯
,
α
T
}
\{{\alpha}_1,{\alpha}_2,\cdots,{\alpha}_T\}
{α1,α2,⋯,αT}
在开始数学推导之前,先简单回顾图像生成模型的本质(上节课其实有讲)。
图像生成模型的本质目标
从一个已知的简单分布,例如:mean是0,每个维度的variance是1的高斯分布,采样出一个向量
z
z
z,丢进网络
G
G
G,得到一张图片:
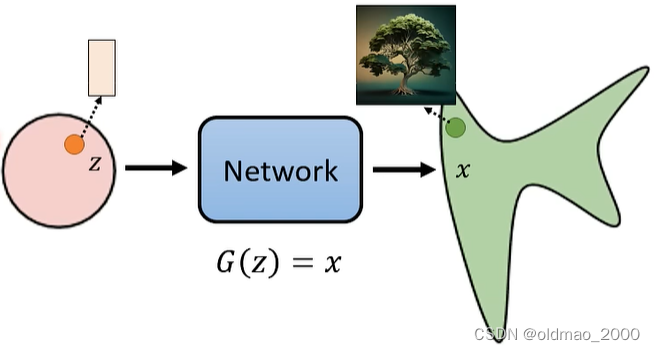
我们希望找到一个网络
G
G
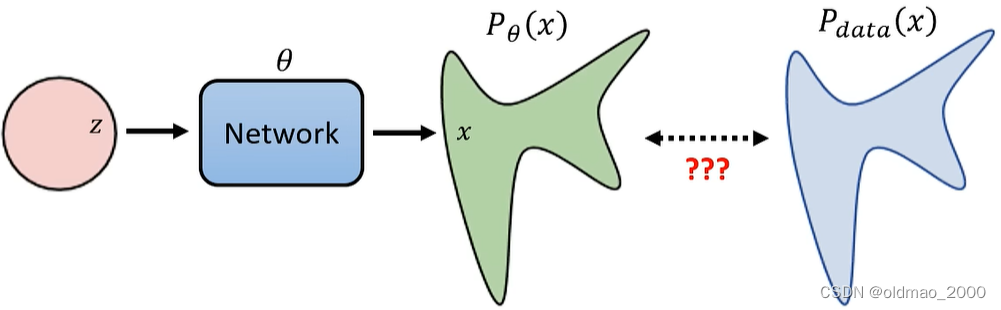
G,使其生成的x与实际图片的分布越接近越好
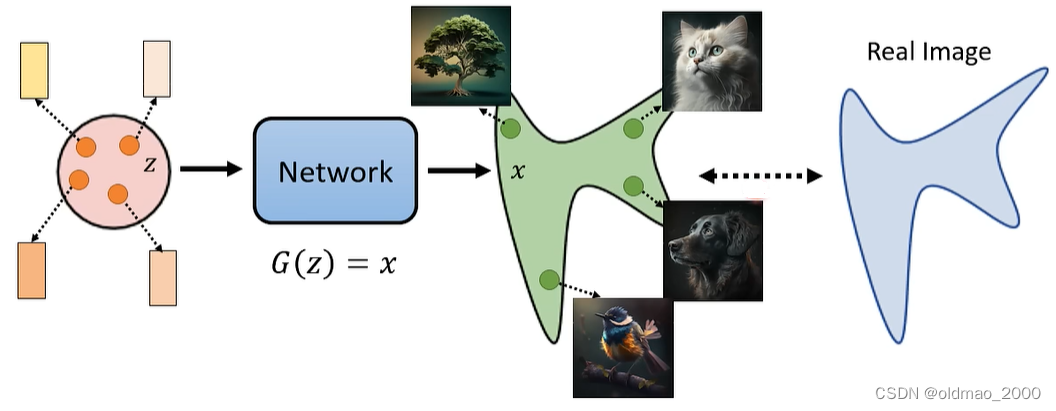
对于文字生成图片任务也类似,只不过是多加了一个文字输入作为限制条件:
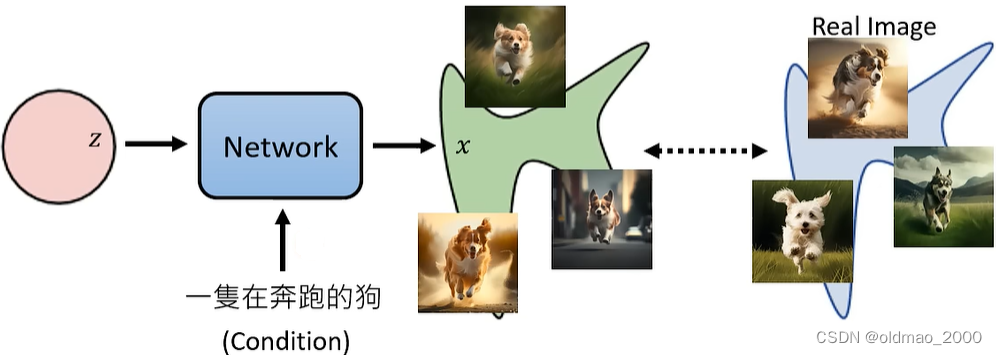
这里一段文字对应的图片可以有无数种答案,因此也是一个分布,比较上面两种模型,有没有其实差异并不大,因此后面的数学推导为了简便,先不考虑文字的输入。
MLE vs KL
上面考虑两个分布越接近越好,在数学上求解一种思路就是使用MLE(Maximum Likelihood Estimation),将网络
G
G
G的参数记为
θ
\theta
θ,则生成图片的结果记为:
P
θ
(
x
)
P_\theta(x)
Pθ(x),而实际图片(训练数据)记为:
P
d
a
t
a
(
x
)
P_{data}(x)
Pdata(x)
则任务可以描述为:
从训练数据
P
d
a
t
a
(
x
)
P_{data}(x)
Pdata(x)采样得到:
{
x
1
,
x
2
,
⋯
,
x
m
}
\{x^1,x^2,\cdots,x^m\}
{x1,x2,⋯,xm},若可计算
P
θ
(
x
i
)
P_\theta(x^i)
Pθ(xi),则根据MLE可知,我们要找到一组参数
θ
∗
\theta^*
θ∗,使得:
θ
∗
=
a
r
g
max
θ
∏
i
=
1
m
P
θ
(
x
i
)
\theta^*=arg\max_\theta \prod_{i=1}^m P_\theta(x^i)
θ∗=argθmaxi=1∏mPθ(xi)
也就是参数
θ
∗
\theta^*
θ∗让网络产生这些真实图片
{
x
1
,
x
2
,
⋯
,
x
m
}
\{x^1,x^2,\cdots,x^m\}
{x1,x2,⋯,xm}的几率最大。
注:这里的
P
θ
(
x
i
)
P_\theta(x^i)
Pθ(xi)实际上无法计算,因为它不是简单几个高斯叠加的GMM,而非常复杂。
证明:最大化MLE与最小化KL等价。
θ
∗
=
a
r
g
max
θ
∏
i
=
1
m
P
θ
(
x
i
)
=
a
r
g
max
θ
log
∏
i
=
1
m
P
θ
(
x
i
)
=
a
r
g
max
θ
∑
i
=
1
m
log
P
θ
(
x
i
)
≈
a
r
g
max
θ
E
x
∼
P
d
a
t
a
[
log
P
θ
(
x
)
]
=
a
r
g
max
θ
∫
x
P
d
a
t
a
(
x
)
log
P
θ
(
x
)
d
x
\begin{aligned}\theta^*&=arg\max_\theta \prod_{i=1}^m P_\theta(x^i)\\ &=arg\max_\theta \log\prod_{i=1}^m P_\theta(x^i)\\ &=arg\max_\theta \sum_{i=1}^m \log P_\theta(x^i)\\ &\approx arg\max_\theta E_{x\sim P_{data}}[\log P_\theta(x)]\\ &= arg\max_\theta \int_x P_{data}(x)\log P_\theta(x)dx \end{aligned}
θ∗=argθmaxi=1∏mPθ(xi)=argθmaxlogi=1∏mPθ(xi)=argθmaxi=1∑mlogPθ(xi)≈argθmaxEx∼Pdata[logPθ(x)]=argθmax∫xPdata(x)logPθ(x)dx
先取对数,然后连乘变累加,结果与求期望值相近似,再根据期望的定义写成积分形式。这里将积分项减去一个与
θ
\theta
θ无关的项,不影响求最大值:
∫
x
P
d
a
t
a
(
x
)
log
P
d
a
t
a
(
x
)
d
x
\int_x P_{data}(x)\log P_{data}(x)dx
∫xPdata(x)logPdata(x)dx
这里
P
d
a
t
a
(
x
)
P_{data}(x)
Pdata(x)只和训练数据有关,与
θ
\theta
θ无关,减去积分项后就可以合并,然后就写成了最小化两个分布KL散度的形式。
=
a
r
g
max
θ
∫
x
P
d
a
t
a
(
x
)
log
P
θ
(
x
)
d
x
=
a
r
g
max
θ
(
∫
x
P
d
a
t
a
(
x
)
log
P
θ
(
x
)
d
x
−
∫
x
P
d
a
t
a
(
x
)
log
P
d
a
t
a
(
x
)
d
x
)
=
a
r
g
max
θ
∫
x
P
d
a
t
a
(
x
)
log
P
θ
(
x
)
P
d
a
t
a
(
x
)
d
x
=
a
r
g
min
θ
K
L
(
P
d
a
t
a
(
x
)
∣
∣
P
θ
(
x
)
)
\begin{aligned} &= arg\max_\theta \int_x P_{data}(x)\log P_\theta(x)dx\\ &=arg\max_\theta \left(\int_x P_{data}(x)\log P_\theta(x)dx\ - \int_x P_{data}(x)\log P_{data}(x)dx\right)\\ &=arg\max_\theta \int_x P_{data}(x)\log \cfrac{P_\theta(x)}{P_{data}(x)}dx\\ &=arg\min_\theta KL\left(P_{data}(x)||P_\theta(x)\right) \end{aligned}
=argθmax∫xPdata(x)logPθ(x)dx=argθmax(∫xPdata(x)logPθ(x)dx −∫xPdata(x)logPdata(x)dx)=argθmax∫xPdata(x)logPdata(x)Pθ(x)dx=argθminKL(Pdata(x)∣∣Pθ(x))
VAE
先回顾 VAE的计算,因为VAE和Diffusion很像,有些推导的过程也可以借鉴。
计算 P θ ( x ) P_\theta(x) Pθ(x)
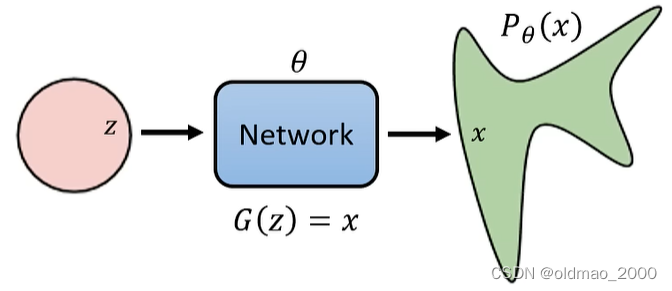
VAE的
P
θ
(
x
)
P_\theta(x)
Pθ(x)可以写成:
P
θ
(
x
)
=
∫
z
P
(
z
)
P
θ
(
x
∣
z
)
d
z
P_\theta(x)=\int_z P(z)P_\theta(x|z)dz
Pθ(x)=∫zP(z)Pθ(x∣z)dz
先求
z
z
z产生的概率,然后求在
z
z
z条件下产生
x
x
x的概率,然后是针对所有
z
z
z进行积分,就得到了
P
θ
(
x
)
P_\theta(x)
Pθ(x)
其中
P
(
z
)
P(z)
P(z)是已知的简单分布,对应上图中的粉红色圈圈。
P
θ
(
x
∣
z
)
P_\theta(x|z)
Pθ(x∣z)如果采用如下定义:
P
θ
(
x
∣
z
)
=
{
1
,
G
(
z
)
=
x
0
,
G
(
z
)
≠
x
P_\theta(x|z)=\begin{cases} 1,\quad G(z)=x \\ 0,\quad G(z)\neq x \end{cases}
Pθ(x∣z)={1,G(z)=x0,G(z)=x
表示
z
z
z通过网络刚好与我们要的图片完全相同,那么就记为1,否则记为0。在图像生成任务这样做会使得上面的表达大概率是0,因为图片即使有1个像素不同也会使得
P
θ
(
x
∣
z
)
=
0
P_\theta(x|z)=0
Pθ(x∣z)=0
解决的方法就是用一个范围来表示网络的输出,如下图所示,
G
(
z
)
G(z)
G(z)表示一个高斯分布的Mean:
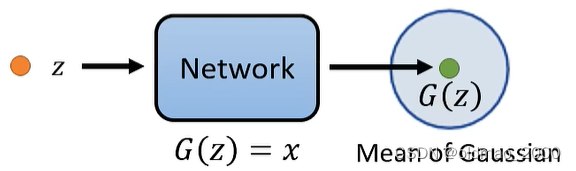
P
θ
(
x
∣
z
)
P_\theta(x|z)
Pθ(x∣z)的定义就变成:
P
θ
(
x
∣
z
)
∝
exp
(
−
∣
∣
G
(
z
)
−
x
∣
∣
2
)
P_\theta(x|z)\propto \exp(-||G(z)-x||_2)
Pθ(x∣z)∝exp(−∣∣G(z)−x∣∣2)
表示
x
x
x与高斯分布中心越近,产生它的概率越大。
Lower bound of log P ( x ) \log P(x) logP(x)
这里讲得比较简略,详细可以看这里:李宏毅学习笔记27.Unsupervised Learning.05: Deep Generative Model (Part II)
需要说明的是:概率
P
θ
(
x
)
P_\theta(x)
Pθ(x)需要网络的参数
θ
\theta
θ才能计算出来,因此把其作为下标,后面很多地方都把下标
θ
\theta
θ进行了省略。
上来直接从损失函数那里往后推:
log
P
θ
(
x
)
=
∫
z
q
(
z
∣
x
)
log
P
(
x
)
d
z
\log P_\theta(x)=\int_zq(z|x)\log P(x)dz
logPθ(x)=∫zq(z∣x)logP(x)dz
由于
log
P
(
x
)
\log P(x)
logP(x)和z无关,由于
∫
z
q
(
z
∣
x
)
d
z
=
1
\int_zq(z|x)dz=1
∫zq(z∣x)dz=1(这里的
q
(
z
∣
x
)
q(z|x)
q(z∣x)是任意一个分布,积分起来就是1),所以等式成立。
=
∫
z
q
(
z
∣
x
)
log
(
P
(
z
,
x
)
P
(
z
∣
x
)
)
d
z
=
∫
z
q
(
z
∣
x
)
log
(
P
(
z
,
x
)
q
(
z
∣
x
)
q
(
z
∣
x
)
P
(
z
∣
x
)
)
d
z
=
∫
z
q
(
z
∣
x
)
log
(
P
(
z
,
x
)
q
(
z
∣
x
)
)
d
z
+
∫
z
q
(
z
∣
x
)
log
(
q
(
z
∣
x
)
P
(
z
∣
x
)
)
d
z
≥
∫
z
q
(
z
∣
x
)
log
(
P
(
z
,
x
)
q
(
z
∣
x
)
)
d
z
=
E
q
(
z
∣
x
)
[
log
(
P
(
x
,
z
)
q
(
z
∣
x
)
)
]
\begin{aligned}&=\int_zq(z|x)\log\left(\frac{P(z,x)}{P(z|x)}\right)dz\\ &=\int_zq(z|x)\log\left(\frac{P(z,x)}{{\color{Blue} q(z|x)}}\frac{{\color{Blue} q(z|x)} }{P(z|x)}\right)dz\\ &=\int_zq(z|x)\log\left(\frac{P(z,x)}{q(z|x)}\right)dz+\int_zq(z|x)\log\left(\frac{q(z|x)}{P(z|x)}\right)dz\\ &\ge \int_zq(z|x)\log\left(\frac{P(z,x)}{q(z|x)}\right)dz=E_{q(z|x)}\left[\log\left(\frac{P(x,z)}{q(z|x)}\right)\right] \end{aligned}
=∫zq(z∣x)log(P(z∣x)P(z,x))dz=∫zq(z∣x)log(q(z∣x)P(z,x)P(z∣x)q(z∣x))dz=∫zq(z∣x)log(q(z∣x)P(z,x))dz+∫zq(z∣x)log(P(z∣x)q(z∣x))dz≥∫zq(z∣x)log(q(z∣x)P(z,x))dz=Eq(z∣x)[log(q(z∣x)P(x,z))]
上面倒数第二行中的最后一项可以看成是两个分布的KL散度,两个分布由于不可能相似,所以该项大于0,所以就写成:
K
L
(
q
(
z
∣
x
)
∣
∣
P
(
z
∣
x
)
)
≥
0
KL(q(z|x)||P(z|x))\geq0
KL(q(z∣x)∣∣P(z∣x))≥0
所以才推导出整个式子的下限,最后可以写成期望的形式,其中的
q
(
z
∣
x
)
q(z|x)
q(z∣x)就是VAE中的Encoder。
DDPM
计算 P θ ( x ) P_\theta(x) Pθ(x)
Diffusion模型生成图片理论上是从一张噪音图片
x
T
x_T
xT开始,不断经过Denoise模块后得到最终结果。

中间第
t
t
t个单步的输入输出可以表示为:
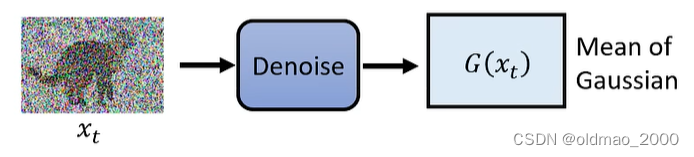
数学上可以写为:
P
θ
(
x
t
−
1
∣
x
t
)
∝
exp
(
−
∣
∣
G
(
x
t
)
−
x
t
−
1
∣
∣
2
)
P_\theta(x_{t-1}|x_t)\propto \exp(-||G(x_t)-x_{t-1}||_2)
Pθ(xt−1∣xt)∝exp(−∣∣G(xt)−xt−1∣∣2)
那么某张图片
x
0
x_0
x0产生的概率可以写为:
P
θ
(
x
0
)
=
∫
x
1
:
x
T
P
(
x
t
)
P
θ
(
x
T
−
1
∣
x
T
)
⋯
P
θ
(
x
t
−
1
∣
x
t
)
⋯
P
θ
(
x
0
∣
x
1
)
d
x
1
:
x
T
P_\theta(x_0)=\int_{x_1:x_T}P(x_t)P_\theta(x_{T-1}|x_T)\cdots P_\theta(x_{t-1}|x_t)\cdots P_\theta(x_{0}|x_1)dx_1:x_T
Pθ(x0)=∫x1:xTP(xt)Pθ(xT−1∣xT)⋯Pθ(xt−1∣xt)⋯Pθ(x0∣x1)dx1:xT
积分号下面的
x
1
:
x
T
x_1:x_T
x1:xT表示从
x
1
x_1
x1到
x
T
x_T
xT逐个计算,上式中的第一个
P
P
P没有下标
θ
\theta
θ,因为噪音
x
T
x_T
xT产生是从简单的高斯分布从采样的,没有经过Denoise模块,与参数
θ
\theta
θ无关。
Lower bound of log P ( x ) \log P(x) logP(x)
原理
DDPM中
log
P
(
x
)
\log P(x)
logP(x)的下界与VAE的推导一样,VAE的推导已省略,要想
Maximize
log
P
θ
(
x
0
)
\text{Maximize} \log P_\theta(x_0)
MaximizelogPθ(x0)
则要提高
log
P
(
x
)
\log P(x)
logP(x)的下界:
Maximize
E
q
(
x
1
:
x
T
∣
x
0
)
[
log
(
P
(
x
0
:
x
T
)
q
(
x
1
:
x
T
∣
x
0
)
)
]
\text{Maximize} E_{q(x_1:x_T|x_0)}\left[\log\left(\frac{P(x_0:x_T)}{q(x_1:x_T|x_0)}\right)\right]
MaximizeEq(x1:xT∣x0)[log(q(x1:xT∣x0)P(x0:xT))]
其中,表示Forward Process的
q
(
x
1
:
x
T
∣
x
0
)
q(x_1:x_T|x_0)
q(x1:xT∣x0)可以写为:
q
(
x
1
:
x
T
∣
x
0
)
=
q
(
x
1
∣
x
0
)
q
(
x
2
∣
x
1
)
⋯
q
(
x
T
∣
x
T
−
1
)
q(x_1:x_T|x_0)=q(x_1|x_0)q(x_2|x_1)\cdots q(x_T|x_{T-1})
q(x1:xT∣x0)=q(x1∣x0)q(x2∣x1)⋯q(xT∣xT−1)
VAE与DDPM二者的下界对比如下图,就不画表格了。
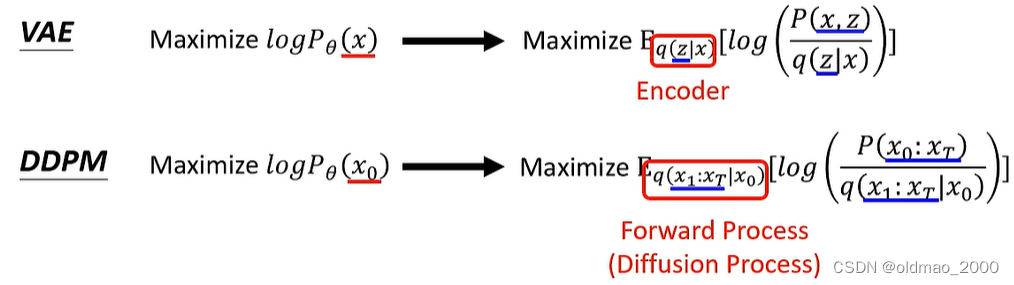
下面来看上面公式中Forward Process中的通项
q
(
x
t
∣
x
t
−
1
)
q(x_t|x_{t-1})
q(xt∣xt−1)如何计算,在DDPM中,
x
t
x_t
xt与
x
t
−
1
x_{t-1}
xt−1的关系如下图所示:
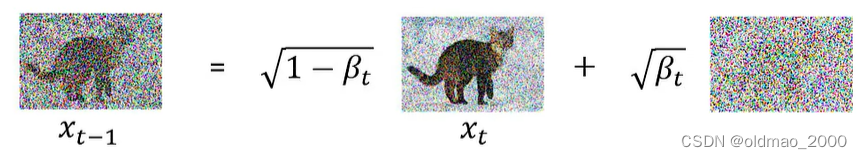
β
1
,
β
2
⋯
,
β
T
\beta_1,\beta_2\cdots,\beta_T
β1,β2⋯,βT是预先定义好的权重值(超参数),用来调整noise的占比,最右边的noise是从
N
(
0
,
I
)
\mathcal{N}(0,I)
N(0,I)中采样得来。
整个
q
(
x
t
∣
x
t
−
1
)
q(x_t|x_{t-1})
q(xt∣xt−1)是一个高斯分布,其Mean为:
1
−
β
t
x
t
\sqrt{1-\beta_t}x_t
1−βtxt,各个维度的Variance都一样,是:
β
t
\sqrt{\beta_t}
βt
Reverse Process的通项
q
(
x
t
∣
x
0
)
q(x_t|x_0)
q(xt∣x0)在理论上应该是一步步计算的:

注:
q
(
x
t
∣
x
0
)
q(x_t|x_0)
q(xt∣x0)的意思是给定清晰图片
x
0
x_0
x0的情况下,得到
x
t
x_t
xt的分布概率。
但是实际上可以选择一步到位,看下图:
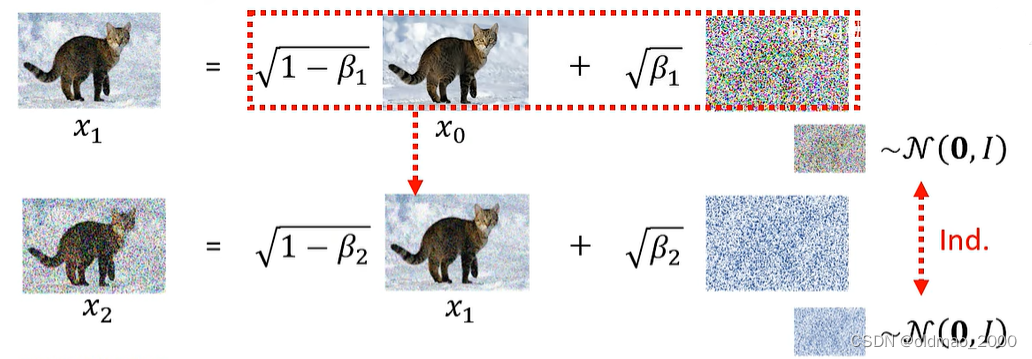
第一行是
x
0
x_0
x0到
x
1
x_1
x1的过程,第二行是
x
1
x_1
x1到
x
2
x_2
x2的过程,两次加的噪音都是从同一个高斯分布中采样出来的,但是是两次独立的采样(红色箭头),然后可以把第一行红框处的部分带入第二行的
x
1
x_1
x1,得到:
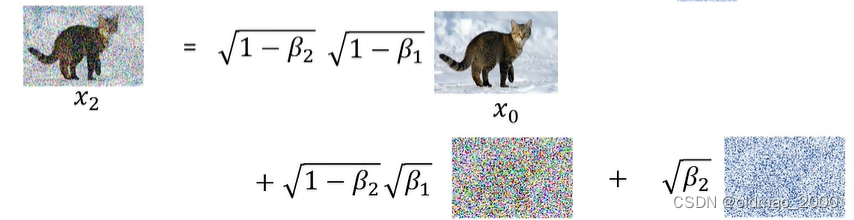
由于两次采样是从同一个高斯分布而来,虽然乘了不同的系数,我们还是可以将两次采样合并为一个采样(如下图的红框合并为黄色采样结果):

这样一来,本来两次的采样就合并为一次了,同理,如果有多次采样,也可以用相同的方法合并为一步到位,只不过前面的系数有变化而已。

如上图所示,第
t
t
t步的
q
(
x
t
∣
x
0
)
q(x_t|x_0)
q(xt∣x0)系数分别为:
1
−
β
1
⋯
1
−
β
t
\sqrt{1-\beta_1}\cdots\sqrt{1-\beta_t}
1−β1⋯1−βt和
1
−
(
1
−
β
1
)
⋯
(
1
−
β
t
)
\sqrt{1-(1-\beta_1)\cdots(1-\beta_t)}
1−(1−β1)⋯(1−βt)
为了简化表达,令:
α
t
=
1
−
β
t
α
ˉ
t
=
α
1
α
2
⋯
α
t
\alpha_t=1-\beta_t\\ \bar\alpha_t=\alpha_1\alpha_2\cdots\alpha_t
αt=1−βtαˉt=α1α2⋯αt
上面的系数就可写成:
α
ˉ
t
1
−
α
ˉ
t
\sqrt{\bar\alpha_t}\\ \sqrt{1-\bar\alpha_t}
αˉt1−αˉt
数学推导
然后就是从论文Understanding Diffusion Models: A Unified Perspective中摘抄过来的下限的推导:
log
P
(
x
)
≥
E
q
(
x
1
:
T
∣
x
0
)
[
log
p
(
x
0
:
T
)
q
(
x
1
:
T
∣
x
0
)
]
=
E
q
(
x
1
:
T
∣
x
0
)
[
log
p
(
x
T
)
∏
t
=
1
T
p
θ
(
x
t
−
1
∣
x
t
)
∏
t
=
1
T
q
(
x
t
∣
x
t
−
1
)
]
=
E
q
(
x
1
:
T
∣
x
0
)
[
log
p
(
x
T
)
p
θ
(
x
0
∣
x
1
)
∏
t
=
2
T
p
θ
(
x
t
−
1
∣
x
t
)
q
(
x
1
∣
x
0
)
∏
t
=
2
T
q
(
x
t
∣
x
t
−
1
)
]
=
E
q
(
x
1
:
T
∣
x
0
)
[
log
p
(
x
T
)
p
θ
(
x
0
∣
x
1
)
∏
t
=
2
T
p
θ
(
x
t
−
1
∣
x
t
)
q
(
x
1
∣
x
0
)
∏
t
=
2
T
q
(
x
t
∣
x
t
−
1
,
x
0
)
]
=
E
q
(
x
1
:
T
∣
x
0
)
[
log
p
(
x
T
)
p
θ
(
x
0
∣
x
1
)
q
(
x
1
∣
x
0
)
+
log
∏
t
=
2
T
p
θ
(
x
t
−
1
∣
x
t
)
q
(
x
t
∣
x
t
−
1
,
x
0
)
]
=
E
q
(
x
1
:
T
∣
x
0
)
[
log
p
(
x
T
)
p
θ
(
x
0
∣
x
1
)
q
(
x
1
∣
x
0
)
+
log
∏
t
=
2
T
p
θ
(
x
t
−
1
∣
x
t
)
q
(
x
t
−
1
∣
x
t
,
x
0
)
q
(
x
t
∣
x
0
)
q
(
x
t
−
1
∣
x
0
)
]
=
E
q
(
x
1
:
T
∣
x
0
)
[
log
p
(
x
T
)
p
θ
(
x
0
∣
x
1
)
q
(
x
1
∣
x
0
)
+
log
∏
t
=
2
T
p
θ
(
x
t
−
1
∣
x
t
)
q
(
x
t
−
1
∣
x
t
,
x
0
)
q
(
x
t
∣
x
0
)
q
(
x
t
−
1
∣
x
0
)
]
=
E
q
(
x
1
:
T
∣
x
0
)
[
log
p
(
x
T
)
p
θ
(
x
0
∣
x
1
)
q
(
x
1
∣
x
0
)
+
log
q
(
x
1
∣
x
0
)
q
(
x
T
∣
x
0
)
+
log
∏
t
=
2
T
p
θ
(
x
t
−
1
∣
x
t
)
q
(
x
t
−
1
∣
x
t
,
x
0
)
]
=
E
q
(
x
1
:
T
∣
x
0
)
[
log
p
(
x
T
)
p
θ
(
x
0
∣
x
1
)
q
(
x
T
∣
x
0
)
+
∑
t
=
2
T
log
p
θ
(
x
t
−
1
∣
x
t
)
q
(
x
t
−
1
∣
x
t
,
x
0
)
]
=
E
q
(
x
1
:
T
∣
x
0
)
[
log
p
θ
(
x
0
∣
x
1
)
]
+
E
q
(
x
1
:
T
∣
x
0
)
[
log
p
(
x
T
)
q
(
x
T
∣
x
0
)
]
+
∑
t
=
2
T
E
q
(
x
1
:
T
∣
x
0
)
[
log
p
θ
(
x
t
−
1
∣
x
t
)
q
(
x
t
−
1
∣
x
t
,
x
0
)
]
=
E
q
(
x
1
∣
x
0
)
[
log
p
θ
(
x
0
∣
x
1
)
]
+
E
q
(
x
T
∣
x
0
)
[
log
p
(
x
T
)
q
(
x
T
∣
x
0
)
]
+
∑
t
=
2
T
E
q
(
x
t
,
x
t
−
1
∣
x
0
)
[
log
p
θ
(
x
t
−
1
∣
x
t
)
q
(
x
t
−
1
∣
x
t
,
x
0
)
]
=
E
q
(
x
1
∣
x
0
)
[
log
p
θ
(
x
0
∣
x
1
)
]
⏟
reconstruction term
−
D
K
L
(
q
(
x
T
∣
x
0
)
∣
∣
p
(
x
T
)
)
⏟
prior matching term
−
∑
t
=
2
T
E
q
(
x
t
∣
x
0
)
[
D
K
L
(
q
(
x
t
−
1
∣
x
t
,
x
0
)
∣
∣
p
θ
(
x
t
−
1
∣
x
t
)
)
]
⏟
denoising matching term
\begin{align*} \log P(x)&\ge E_{q(x_{1:T}|x_0)}\left[\log\frac{p(x_{0:T})}{q(x_{1:T}|x_0)}\right]\\ &=E_{q(x_{1:T}|x_0)}\left[\log\frac{p(x_T)\prod_{t=1}^Tp_\theta(x_{t-1}|x_t)}{\prod_{t=1}^Tq(x_t|x_{t-1})}\right]\\ &=E_{q(x_{1:T}|x_0)}\left[\log\frac{p(x_T)p_\theta(x_0|x_1)\prod_{t=2}^Tp_\theta(x_{t-1}|x_t)}{q(x_1|x_0)\prod_{t=2}^Tq(x_t|x_{t-1})}\right]\\ &=E_{q(x_{1:T}|x_0)}\left[\log\frac{p(x_T)p_\theta(x_0|x_1)\prod_{t=2}^Tp_\theta(x_{t-1}|x_t)}{q(x_1|x_0)\prod_{t=2}^Tq(x_t|x_{t-1},x_0)}\right]\\ &=E_{q(x_{1:T}|x_0)}\left[\log\frac{p(x_T)p_\theta(x_0|x_1)}{q(x_1|x_0)}+\log\prod_{t=2}^T\cfrac{p_\theta(x_{t-1}|x_t)}{q(x_t|x_{t-1},x_0)}\right]\\ &=E_{q(x_{1:T}|x_0)}\left[\log\frac{p(x_T)p_\theta(x_0|x_1)}{q(x_1|x_0)}+\log\prod_{t=2}^T\cfrac{p_\theta(x_{t-1}|x_t)}{\cfrac{q(x_{t-1}|x_t,x_0)q(x_t|x_0)}{q(x_{t-1}|x_0)}}\right]\\ &=E_{q(x_{1:T}|x_0)}\left[\log\frac{p(x_T)p_\theta(x_0|x_1)}{q(x_1|x_0)}+\log\prod_{t=2}^T\cfrac{p_\theta(x_{t-1}|x_t)}{\cfrac{q(x_{t-1}|x_t,x_0)\cancel{q(x_t|x_0)}}{\cancel{q(x_{t-1}|x_0)}}}\right]\\ &=E_{q(x_{1:T}|x_0)}\left[\log\frac{p(x_T)p_\theta(x_0|x_1)}{\cancel{q(x_1|x_0)}}+\log\cfrac{\cancel{q(x_1|x_0)}}{q(x_T|x_0)}+\log\prod_{t=2}^T\cfrac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}\right]\\ &=E_{q(x_{1:T}|x_0)}\left[\log\frac{p(x_T)p_\theta(x_0|x_1)}{q(x_T|x_0)}+\sum_{t=2}^T\log\cfrac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}\right]\\ &=E_{q(x_{1:T}|x_0)}\left[\log p_\theta(x_0|x_1)\right] +E_{q(x_{1:T}|x_0)}\left[\log\frac{p(x_T)}{q(x_T|x_0)}\right] +\sum_{t=2}^TE_{q(x_{1:T}|x_0)}\left[\log\cfrac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}\right]\\ &=E_{q(x_1|x_0)}\left[\log p_\theta(x_0|x_1)\right] +E_{q(x_T|x_0)}\left[\log\frac{p(x_T)}{q(x_T|x_0)}\right] +\sum_{t=2}^TE_{q(x_t,x_{t-1}|x_0)}\left[\log\cfrac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}\right]\\ &=\underset{\text{reconstruction term}}{\underbrace{E_{q(x_1|x_0)}\left[\log p_\theta(x_0|x_1)\right]}} -\underset{\text{prior matching term}}{\underbrace{D_{KL}(q(x_T|x_0)||p(x_T))}} -\sum_{t=2}^T\underset{\text{denoising matching term}}{\underbrace{E_{q(x_t|x_0)}\left[D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t)) \right]}} \end{align*}
logP(x)≥Eq(x1:T∣x0)[logq(x1:T∣x0)p(x0:T)]=Eq(x1:T∣x0)[log∏t=1Tq(xt∣xt−1)p(xT)∏t=1Tpθ(xt−1∣xt)]=Eq(x1:T∣x0)[logq(x1∣x0)∏t=2Tq(xt∣xt−1)p(xT)pθ(x0∣x1)∏t=2Tpθ(xt−1∣xt)]=Eq(x1:T∣x0)[logq(x1∣x0)∏t=2Tq(xt∣xt−1,x0)p(xT)pθ(x0∣x1)∏t=2Tpθ(xt−1∣xt)]=Eq(x1:T∣x0)[logq(x1∣x0)p(xT)pθ(x0∣x1)+logt=2∏Tq(xt∣xt−1,x0)pθ(xt−1∣xt)]=Eq(x1:T∣x0)
logq(x1∣x0)p(xT)pθ(x0∣x1)+logt=2∏Tq(xt−1∣x0)q(xt−1∣xt,x0)q(xt∣x0)pθ(xt−1∣xt)
=Eq(x1:T∣x0)
logq(x1∣x0)p(xT)pθ(x0∣x1)+logt=2∏Tq(xt−1∣x0)
q(xt−1∣xt,x0)q(xt∣x0)
pθ(xt−1∣xt)
=Eq(x1:T∣x0)[logq(x1∣x0)
p(xT)pθ(x0∣x1)+logq(xT∣x0)q(x1∣x0)
+logt=2∏Tq(xt−1∣xt,x0)pθ(xt−1∣xt)]=Eq(x1:T∣x0)[logq(xT∣x0)p(xT)pθ(x0∣x1)+t=2∑Tlogq(xt−1∣xt,x0)pθ(xt−1∣xt)]=Eq(x1:T∣x0)[logpθ(x0∣x1)]+Eq(x1:T∣x0)[logq(xT∣x0)p(xT)]+t=2∑TEq(x1:T∣x0)[logq(xt−1∣xt,x0)pθ(xt−1∣xt)]=Eq(x1∣x0)[logpθ(x0∣x1)]+Eq(xT∣x0)[logq(xT∣x0)p(xT)]+t=2∑TEq(xt,xt−1∣x0)[logq(xt−1∣xt,x0)pθ(xt−1∣xt)]=reconstruction term
Eq(x1∣x0)[logpθ(x0∣x1)]−prior matching term
DKL(q(xT∣x0)∣∣p(xT))−t=2∑Tdenoising matching term
Eq(xt∣x0)[DKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt))]
原文公式51的第一个
p
p
p多了一个
θ
\theta
θ
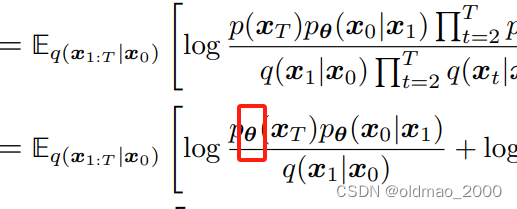
上面的结果中的第二项prior matching term可以忽略,原文中直接给0值,这项是衡量两个分布的相似度,一个分布是从搞屎采样出来的噪音
x
T
x_T
xT,另外是给定清晰图片
x
0
x_0
x0进行diffusion process得到
x
T
x_T
xT的过程,该过程由我们自己操控,两个分布毫无相似度,因此为0。李老师在这里的解释是因为该表达式中没有包含网络参数
θ
\theta
θ,因此与要最大化的下限无关,可以忽略。
现在的下限等于第一项(reconstruction term)减去第三项(denoising matching term),要使得整体最大化,就是要第一项越大越好,第三项越接近0越好,这里推导第一项的过程与第三项相似,因此只推导第三项。
写到这里由于字数太多,需要令开一篇。