---

一、题目描述

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

二、示例与提示

示例 1：

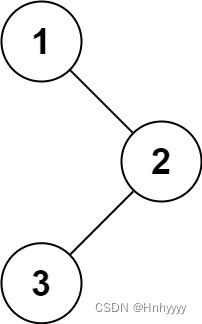
输入： root = [1,null,2,3]
输出： [1,3,2]

示例 2：

输入： root = []
输出： []

示例 3：

输入： root = [1]
输出： [1]

提示

1. 树中节点数目在范围 [0, 100] 内
2. -100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

三、思路

1. 递归法

" 一入递归深似海，从此offer是路人~ "

递归法代码是很简单，但是很多同学并没有总结出做递归题的方法论，这里帮助大家确定下来递归法的三要素。

1）确定递归函数的参数和返回值
2）确定终止条件
3）确定单层递归的逻辑

---

2. 迭代法

为什么可以用迭代法（非递归的方式） 来实现二叉树的前后中序遍历呢？

这是因为递归的实现就是：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。

所以我们知道用栈也可以实现二叉树的前后中序遍历。

首先，中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是把节点的数值放进result数组中），这就造成了处理顺序和访问顺序是不一致的。

那么在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素。

总结一下，在迭代的过程中，其实我们有两个操作：

1. 访问（指针）：遍历节点
2. 处理（栈）：将元素放进result数组中

四、代码

1. 递归法

// 递归函数参数和返回值
void inorder(struct TreeNode* node,int* ret,int* returnSize){
	// 递归终止条件
    if(node==NULL)
    return;
    // 单层递归逻辑
    inorder(node->left,ret,returnSize); //左
    // 注意 * 和 ++ 优先级（从右向左），所以此处要加括号
    ret[(*returnSize)++]=node->val; //中
    inorder(node->right,ret,returnSize); //右
}

int* inorderTraversal(struct TreeNode* root, int* returnSize){
    int* ret=malloc(sizeof(int)* 100);
    *returnSize=0;
    // 调用递归函数
    inorder(root,ret,returnSize);
    // 返回最终数组地址
    return ret;
}

复杂度分析

时间复杂度： O(n)

2. 迭代法

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int>res; // 最终返回的res数组
        stack<TreeNode*>st; // 栈用来处理节点
        TreeNode* cur = root; // 指针用来访问节点（遍历整颗树）
        // 若当前访问节点不为空或栈不为空则继续遍历
        while(cur != NULL || !st.empty()) {
        	// 当前节点不为空则放入栈中，继续遍历
            if (cur != NULL) {
                st.push(cur);
                cur = cur->left; //左
            }
            // 当前节点为空则通过栈来处理节点（将栈顶元素的数值放进result数组中）
            else {
                cur = st.top();
                st.pop();
                res.push_back(cur->val); //中
                cur = cur->right; //右
            }
        }
        // 返回res数组
        return res;
    }
};

复杂度分析

时间复杂度： O(n)