标题

JADE: Adaptive Differential Evolution with Optional External Archive

摘要

提出了一种新的差分进化（DE）算法 JADE，通过实施具有可选外部存档的新变异策略“DE/current-to-pbest”来提高优化性能，并以自适应方式更新控制参数。DE/current-to- pbest是经典“DE/current-to-best”的推广，而可选的存档操作利用历史数据来提供进化方向信息。这两种操作都使人口多样化并提高收敛性能。参数自适应自动将控制参数更新为合适的值，并避免用户先验了解参数设置与优化问题特征之间的关系。因此有助于提高算法的鲁棒性。仿真结果表明，在 20 个基准问题的收敛性能方面，JADE 优于或至少与其他经典或自适应 DE 算法、规范粒子群优化和文献中的其他进化算法相媲美。具有外部存档的 JADE 对于相对高维问题显示出有希望的结果。此外，它清楚地表明，不存在适合各种问题甚至单个问题的不同优化阶段的固定控制参数设置。

关键字

自适应参数控制、差分进化、进化优化、外部存档。

结论

研究背景

I. INTRODUCTION

差分进化（DE）已被证明是一种简单而有效的进化算法，适用于现实应用中的许多优化问题[1]-[5]。然而，根据实验研究[6]和理论分析[7]，其性能仍然相当依赖于突变因子和交叉概率等控制参数的设置。尽管已经有参数设置的建议[2]、[6]、[8]，但参数设置和优化性能之间的相互作用仍然很复杂并且尚未完全理解。这主要是因为没有适合各种问题甚至单个问题不同演化阶段的固定参数设置。

用于调整控制参数的试错法通常需要繁琐的优化试验，即使对于在整个进化搜索过程中固定其参数的算法（例如经典的 DE/rand/1/bin）也是如此。出于这种考虑，最近引入了不同的自适应或自适应机制来动态更新控制参数，而无需用户事先了解参数设置与优化问题特征之间的关系。此外，参数自适应如果设计得当，能够提高算法的收敛性能。

在前述参考文献中提出的参数自适应机制可以基于控制参数如何改变来分类。
三类参数控制机制解释如下。

• 确定性参数控制：控制参数由一些确定性规则改变，而不考虑来自进化搜索的任何反馈。一个例子是 Holland 提出的突变率随时间的变化[22]。
• 自适应参数控制：来自进化搜索的反馈用于动态改变控制参数。此类的例子有 Rechenberg 的“1/5 规则”[23] 以及 [11] 和 [12] 中的模糊逻辑自适应 DE。
• 自适应参数控制：采用“进化评估”的方法进行控制参数的自适应。控制参数与个体直接相关并经历突变和重组/交叉。由于更好的参数值往往会产生更有可能生存的个体，因此这些值可以传播给更多的后代。

如果设计得当，自适应或自适应参数控制可以通过动态调整参数以适应不同适应度环境的特征来增强算法的鲁棒性。因此，它适用于各种优化问题，无需反复试验。此外，如果在特定问题的不同演化阶段将控制参数调整为适当的值，则可以提高收敛速度。

对于许多基准问题[13]-[17]，自适应和自适应DE算法比没有参数控制的经典DE算法表现出更快、更可靠的收敛性能。找到最合适的 DE 变体并将其用作可以引入参数自适应操作的底层方案是很有意义的。一些自适应算法[10]、[14]、[18]是基于经典的DE/rand/1/bin开发的，已知该算法具有鲁棒性，但在收敛速度方面效率较低。其他人[13]、[14]、[16]同时实现DE/rand/1/bin和一个或多个贪婪DE变体，例如 DE/current-to-best/1/bin，并动态更新使用每个变体的概率以产生后代。

到目前为止，还没有完全基于贪婪 DE 变体（例如 DE/current-to-best/1/bin 和 DE/best/1/bin）开发出利用最佳解决方案信息的方法在目前的人口中。原因似乎很简单：贪婪变体通常不太可靠，并且可能导致过早收敛等问题，特别是在解决多模态问题时 [8]、[24]。然而，我们注意到，精心设计的参数自适应方案通常有利于增强算法的鲁棒性。因此，在自适应 DE 算法中，贪婪 DE 变体的可靠性变得不太重要，而它们的快速收敛变得更具吸引力。

除了当前群体中的最佳解决方案之外，历史数据是可用于提高收敛性能的另一个来源。一个例子是粒子群优化（PSO）[25]，其中历史上探索的最佳解决方案被用来指导当前群体（群体）的移动。在本文中，我们感兴趣的不是之前探索的最佳解决方案，而是一组最近探索的较差解决方案，并将它们与当前群体的差异视为实现最优的有希望的方向。这些解决方案还用于改善人口多样性。

鉴于上述考虑，我们引入了一种新的贪婪变异策略，即带有可选外部存档的“DE/current-to-pbest”，并将其作为我们参数自适应算法JADE的基础。 [26] 中提出了 JADE 算法的早期版本。作为DE/current-tobest的推广，DE/current-tobest不仅利用了最佳解的信息，还利用了其他好的解的信息。具体来说，可以在DE/current-to-pbest中随机选择前100p%，p ∈ (0, 1],解中的任意一个，以起到DE/currentto-best中专门为单个最佳解设计的作用。此外，可以将归档的劣解与当前种群之间的差异纳入变异操作中，尽管具有贪心性质，但该策略能够使种群多样化，从而缓解早熟收敛等问题。通过自适应参数控制，进一步提高了算法的可靠性。

本文的其余部分安排如下。第二节描述了差分进化的基本过程，并介绍了有助于回顾第三节中的各种自适应或自适应 DE 算法的符号和术语。新算法 JADE 在第四节中详细阐述，详细解释了具有可选存档的 DE/current-topbest 和自适应参数控制机制。仿真结果在第五节中给出，用于将 JADE 与其他进化算法进行比较。最后，第六节总结了结论性意见。

常用基础理论知识

II. BASIC OPERATIONS OF DE

在本节中，我们描述差分进化的基本操作，并介绍必要的符号和术语，以方便稍后解释不同的自适应差分进化算法。

差分进化遵循进化算法的一般过程：生成初始种群，交叉，变异，选择。

变异策略：

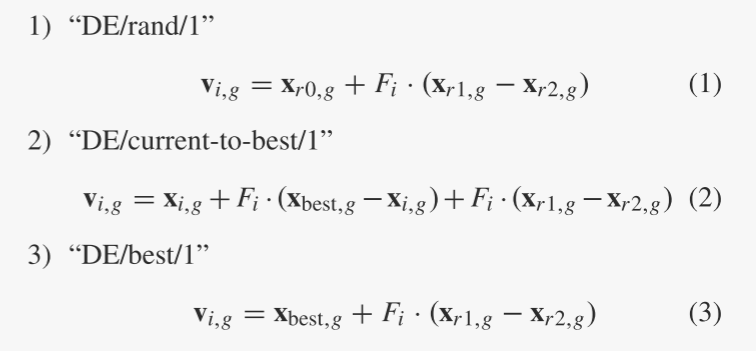
应当注意，试验向量的某些分量可能违反预定义的边界约束。解决这个问题的可能解决方案包括重置方案、惩罚方案等。然而，约束问题不是本文的主要关注点。因此，我们遵循一个简单的方法，将违规组件设置为违规边界的中间和父个体的相应组件[2]，即

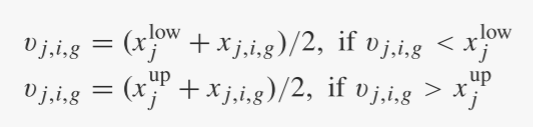
交叉：突变后，二项式交叉操作形成最终的试验/后代向量

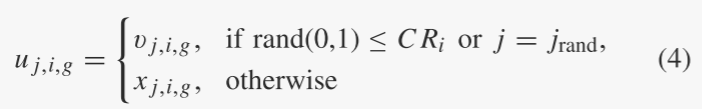
选择：选择操作根据父向量和试验向量的适应度值选择较好的一个。例如，如果我们有一个最小化问题，则所选向量由下式给出:

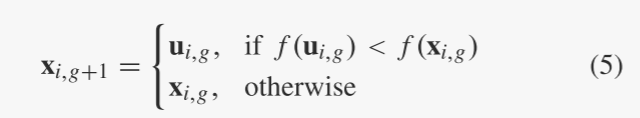
上述一对一选择过程在不同的DE算法中通常保持固定，而交叉可以有除(4)中的二项式运算之外的变体。因此，经典的差分进化算法历史上被命名为DE/rand/1/bin，寓意其DE/rand/1变异策略和二项式交叉操作。

III. ADAPTIVE DE ALGORITHMS

本节简要回顾了一些最新的自适应和自适应 DE 算法，这些算法随着进化搜索的进行而动态更新控制参数。它提供了一种方便的方法来将这些参数自适应机制与后来在 JADE 中提出的参数自适应机制进行比较。

A. DESAP

在[10]中，提出了一种算法 DESAP，不仅可以动态调整突变和交叉参数 η 和 δ（这通常是其他自适应或自适应算法中的情况），还可以动态调整种群大小 π。 DESAP的基本策略与经典的DE/rand/1/bin略有不同，与[9]中介绍的方案相当相似——而δ和π分别与CR和NP具有相同的含义，η指的是概率交叉后应用额外的正态分布突变。普通突变因子 F 在 DESAP 中确实保持固定。

在 DESAP 中，每个个体 i 都与其自己的控制参数 δi 、 ηi 和 πi 相关联。这些参数以类似于相应向量 xi 的方式进行交叉和变异。如果 f(ui)< f(xi )，则这些控制参数的新值与 ui 一起保留。尽管推理简单，但 DESAP 的性能并不令人满意。它仅在五个 De Jong 测试问题之一上优于传统 DE，而其他结果非常相似。事实上，正如作者所说，DESAP 主要用于证明通过自适应更新种群规模以及其他控制参数来进一步减少控制参数的可能性。

B. FADE

Liu 和 Lampinen [11] 提出的模糊自适应微分进化（FADE）是 DE 的一种新变体，它使用模糊逻辑控制器来调整控制参数 Fi 和 CRi 以进行变异和交叉操作。类似的方法也被独立提出用于多目标DE优化[12]。与许多其他自适应 DE 算法（除 DESAP [10] 外）类似，假设种群大小预先调整并在 FADE 的整个进化过程中保持固定。模糊逻辑控制方法通过一组 10 个标准基准函数进行了测试，当问题维度较高时，该方法显示出比经典 DE 更好的结果。

C. SaDE

SaDE[13]是由Qin和Suganthan提出的，用于同时实现两种变异策略“DE/rand/1”和“DE/current-to-best/1”。它根据过去 50 代的成功率来调整两种策略产生后代的概率。人们相信，这种适应过程可以在不同的学习阶段针对所考虑的问题逐渐演化出最合适的突变策略。这类似于[27]、[28]中提出的方案，其中竞争启发式（包括几种DE变体、单纯形）方法和进化策略）同时采用，并且通过任何这些启发法产生后代的概率是动态调整的。

在 SaDE 中，每一代的突变因子按照均值 0.5、标准差 0.3 的正态分布独立生成，并截断到区间 (0, 2]。表明该方案可以保持局部（Fi 值较小） ）和全局（具有较大 Fi 值）搜索能力，在整个进化过程中生成潜在的良好突变向量。交叉概率根据独立正态分布随机生成，平均 CRm 和标准差为 0.1。与 Fi 相反，CRi在下一次重新生成之前，值在五代中保持固定。平均 CRm 初始化为 0.5。为了使 CR 适应适当的值，作者根据自上次 CRm 更新以来记录的成功 CR 值每 25 代更新一次 CRm。

为了加快 SaDE 的收敛速度，作者进一步对 200 代后的一些优秀个体应用了局部搜索程序（拟牛顿法）。

虽然 SaDE 最初是为了解决无约束优化问题而提出的，但通过在解决一组约束优化问题时实施五种候选变异策略来进一步扩展 SaDE [14]。

D. jDE

布雷斯特等人 [15]提出了一种新的自适应DE，jDE，它是基于经典DE/rand/1/bin。与其他方案类似，jDE 在优化过程中固定种群大小，同时调整与每个个体相关的控制参数 Fi 和 CRi。初始化过程为每个个体设置 Fi = 0.5 和 CRi = 0.9。 jDE 不是 SaDE 的随机化 Fi 和 CRi 并通过记录的成功值更新 CRm 的方法，而是根据 [0.1, 1] 和 [0,1] 上的均匀分布重新生成（每代概率 τ1 = τ2 = 0.1）Fi 和 CRi 的新值。人们相信，更好的参数值往往会产生更有可能生存的个体，因此这些值应该传播到下一代。

实验结果表明，jDE 的性能明显优于经典的 DE/rand/1/bin、FEP 和 CEP [29]、自适应 LEP 和 Best Levy [30] 以及 FADE 算法 [11]。 jDE 通过采用两种变异策略进一步扩展，名为 jDE-2 [17] 的新算法在一组 25 个基准函数上显示出与原始 SaDE（在 200 代后实现局部拟牛顿搜索过程）竞争的结果。

研究内容、成果

IV. JADE

在本节中，我们提出了一种新的 DE 算法 JADE，它实现了带有可选存档的变异策略“DE/current-to- pbest”，并以自适应方式控制 F 和 CR。 JADE 采用与第二节（4）和（5）中描述的相同的交叉和选择操作。

A. DE/Current-to-pbest

DE/rand/1是第一个针对DE开发的突变策略[1]、[2]，据说是文献中最成功、使用最广泛的方案[31]。然而，[6]表明DE/best/2可能比DE/rand/1有一些优势，并且[32]对于研究的大多数技术问题更倾向于DE/best/1。此外，[33] 的作者认为，合并最佳解决方案信息是有益的，并在他们的算法中使用 DE/current-to-best/1。

与 DE/rand/k 相比，DE/current-to-best/k 和 DE/best/k 等贪婪策略通过在进化搜索中纳入最佳解决方案信息，受益于其快速收敛。然而，最佳解信息也可能因种群多样性减少而导致过早收敛等问题。

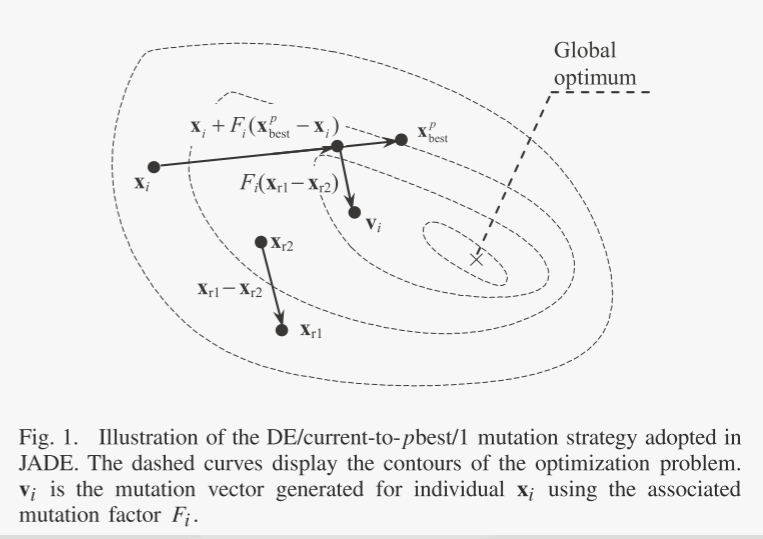
鉴于现有贪婪策略（2）和（3）收敛速度快但可靠性较差，提出了一种新的变异策略，称为DE / current-to-pbest ，作为自适应DE的基础本文提出的算法JADE。如图1所示，在DE/current-to-pbest/1（无存档）中，突变向量按以下方式生成：

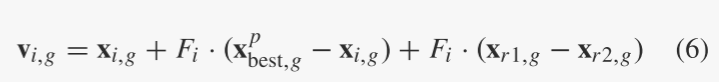
与当前群体相比，最近探索的较差解决方案提供了有关有希望的进展方向的更多信息。将 A 表示为存档的劣质解集，将 P 表示为当前总体。在 DE/current-to-pbest/1 with archive 中，突变向量生成如下：

归档操作变得非常简单，以避免大量的计算开销。存档初始化为空。然后，在每一代之后，在（5）的选择过程中失败的父解决方案被添加到档案中。如果存档大小超过某个阈值（例如 NP），则从存档中随机删除一些解决方案以将存档大小保持为 NP。很明显，（6）是（7）的特殊情况，将存档大小设置为零。

该档案提供了有关进展方向的信息，也能够提高人口的多样性。此外，如后面的参数自适应操作（10）-（12）所示，我们鼓励大的 F 值，这有助于增加种群多样性。因此，尽管它偏向潜在最优（可能是局部最小值）的方向，但所提出的 DE/currentto-pbest/1 不容易陷入局部最小值。作为一个简单的比较，DE/rand/1 搜索相对较小的区域，不偏向任何特殊方向，而带有存档的 DE/current-to-pbest/1 搜索相对较大的区域，偏向有希望的进展方向。
JADE的伪代码如表1所示。接下来我们介绍F和CR的参数适配。

B. Parameter Adaptation

在每一代g中，每个个体xi的交叉概率CRi是根据均值μCR和标准差0.1的正态分布独立生成的:

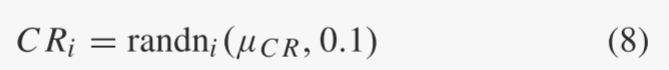
然后截断为 [0, 1]。将 SCR 表示为 g 代所有成功交叉概率 CRi 的集合。这平均 μCR 初始化为 0.5，然后在每代结束时更新为

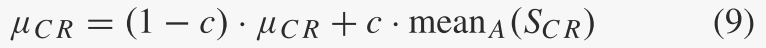
类似地，在每一代g，每个个体xi的突变因子Fi是根据位置参数μF和尺度参数0.1的柯西分布独立生成的：

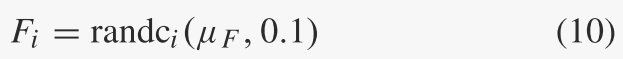
如果 Fi ≥ 1，则截断为 1；如果 Fi ≤ 0，则重新生成。将 SF 表示为 g 代中所有成功突变因子的集合。柯西分布的位置参数 μF 初始化为 0.5，然后在每代结束时更新为：

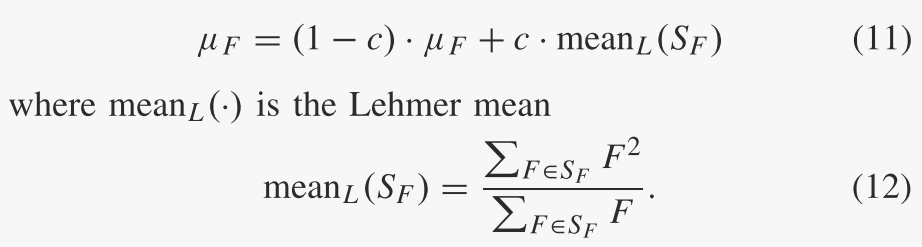
C. Explanations of the Parameter Adaptation

μCR的适配基于以下原则。更好的控制参数值往往会产生更有可能生存的个体，因此这些值应该传播给后代。因此，基本操作是记录最近成功的交叉概率并用它们来指导新 CRi 的生成(8)中的标准差设置得相对较小，因为否则自适应就不能有效地发挥作用；例如，在无限标准导数的极端情况下，截断正态分布变得与 μCR 的值无关。

与 CR 相比，μF 的适应有两个不同的操作。首先，Fi 是根据截断柯西分布生成的。与正态分布相比，柯西分布更有利于使突变因素多样化，从而避免贪婪突变策略（例如DE/best、DE/current-to-best、DE/current-to-best、DE/current-to-pbest）中经常出现的过早收敛。如果突变因子高度集中在某个值附近。

其次，μF 的适应通过使用（12）中的 Lehmer 平均值而不是 μCR 适应中使用的算术平均值，对更大的成功突变因子给予更多的权重。因此，Lehmer 均值有助于传播更大的突变因子，从而提高进展率。相反，SF的算术平均值往往小于突变因子的最优值，从而导致μF较小，导致最终早熟收敛。 μF 趋于较小的趋势主要是由于进化搜索的成功概率和进度之间的差异。事实上，小 Fi 的 DE/current-to-pbest 类似于 (1 + 1) 进化策略 (ES) [23]，因为两者都在基向量的小邻域中生成后代。对于(1 + 1) ES，已知突变方差越小，通常成功的概率越高（这对于走廊和球体函数[23]、[34]来说是严格证明的）。然而，接近 0 的突变方差显然会导致微不足道的进化进程。一种简单而有效的方法是对较大的成功突变因子给予更多的权重，以便在进化搜索中取得更快的进展。

对于(9)和(11)中的常数c，如果c = 0，则不会发生参数自适应。否则，成功的CRi或Fi的寿命大约为1/c代；即，在 1/c 代之后，当 c 接近于零时，μCR 或 μF 的旧值减小了 (1 − c)^1/c → 1/e ≈ 37%

D. Discussion of Parameter Settings

经典DE有两个控制参数F和CR需要用户调整。众所周知，这些参数是与问题相关的，因此通常需要进行繁琐的试验和错误才能找到针对每个特定问题的适当值。相反，预计JADE的两个新参数c和p根据它们在JADE中的角色对不同的问题不敏感：c控制参数适应的速率，p决定变异策略的贪婪程度。如第五节所示，JADE 通常在 1/c ∈ [5, 20] 和 p ∈ [5%, 20%] 时表现最好；即μCR和μF值的寿命范围为5到20代，我们考虑突变中前5-20％的高质量解决方案。

V. SIMULATION

在本节中，JADE 用于最小化一组 13 个维度 D = 30 或 100 [29]、[35] 的可扩展基准函数以及一组较低维度 D = 2 ∼ 6 [36] 的 Dixon-Szegö 函数，如表二和表三所示。

JADE 与最近的两种自适应 DE 算法 jDE 和 SaDE、经典的 DE/rand/1/bin 和规范的 PSO 算法 [37] 进行了比较。它还与它的两种变体 rand-JADE 和 nona-JADE 进行比较，以确定其不同组件的优点。为了公平比较，我们在所有模拟中将 JADE 的参数设置为固定，p = 0.05 和 c = 0.1。我们遵循jDE[15]和SaDE[13]原论文中的参数设置，只是SaDE中禁用了拟牛顿局部搜索。对于 PSO，参数值选自 [37]，因为它们通常比我们研究的其他文献中提出的值效果更好。 DE/rand/1/bin 的参数设置为 F = 0.5 和 CR = 0.9，如[1]、[8]、[15]、[38]中使用或推荐的。

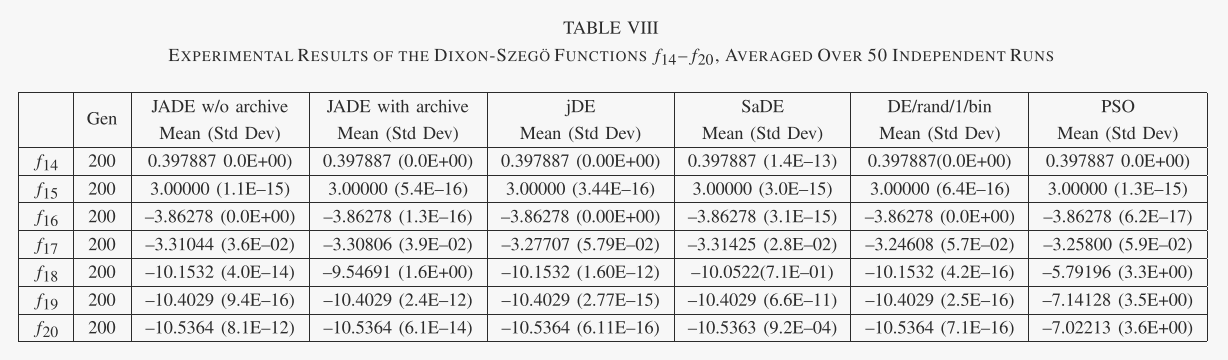
表 II 总结了 13 个可扩展的基准函数。虽然所有这些函数都有一个最优值 f* = 0，但一些不同的特征简要总结如下。 f1–f4 是连续单峰函数。 f5 是 Rosenbrock 函数，对于 D = 2 和 3 是单峰的，但在高维情况下可能有多个最小值 [39]。 f6 是不连续阶跃函数，f7 是噪声四次函数。 f8-f13 是多峰的，其局部最小值的数量随着问题维度呈指数增加[29]。此外，f8 是本文研究的唯一有界约束函数。表 III 简要描述了多峰 Dixon-Szegö 函数的特征。有兴趣的读者可以参考[36]了解详细信息。

在所有模拟中，在 D ≤ 10、= 30 和 = 100 的情况下，我们将种群大小 NP 分别设置为 30、100 和 400。本节报告的所有结果均基于 50 次独立运行而获得。、

为了清楚起见，最佳和次佳算法的结果分别以粗体和斜体标记；如果不是所有或大多数算法产生相同的结果。

A. Comparison of JADE With Other Evolutionary Algorithms

表 IV 和表 V 总结了 f1-f13 每种算法获得的结果的平均值和标准差。这些统计数据仅在优化结束时计算 f1-f4 和 f7。对于其他函数，也会报告中间结果，因为由于 MATLAB 的精度问题，不同算法获得的最终结果可能相同于零或一定的残差（参见图 3 中 f10 和 f13 的误差平台）。在这些情况下，仅比较中间结果，并且可能以粗体或斜体标记。

在表六和表七中，我们总结了每种算法的成功率（SR）和成功运行的函数评估平均次数（FESS）。如果以足够的精度找到最佳解决方案，则实验被认为是成功的：噪声函数 f7 为 10⁻²，所有其他函数为 10⁻⁸。 FESS 和 SR 可分别用于比较不同算法的收敛速度（在成功运行中）和可靠性。

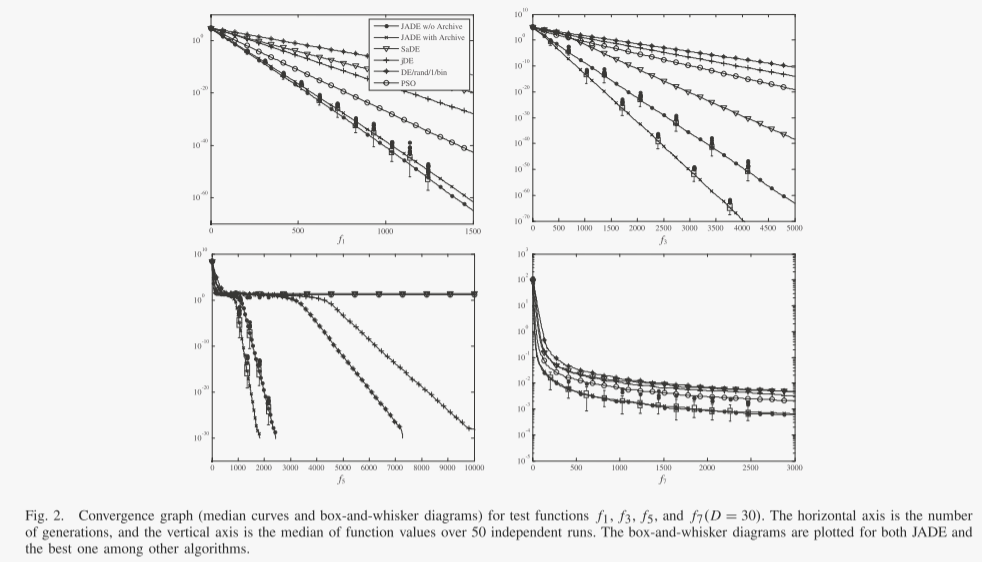
为了便于说明，我们在图 2 和 3 中绘制了一些 30 维和 100 维问题的收敛图。分别为2和3。请注意，在这些图中，我们绘制了中值曲线（而不是表中报告的平均值），因为当算法仅偶尔导致错误收敛时，这些曲线与盒须图一起提供了更多信息。盒须图是在某些代中绘制的最佳和次佳算法。这有助于说明 50 次独立运行结果的分布情况。

关于不同算法的收敛速度和可靠性的重要观察可以从图 1 和 2 中给出的结果中得到。 2 和 3，以及表 IV 和 V。首先，这些结果表明，对于问题集 f1-f13，有或没有存档的 JADE 的总体收敛速度是最好的，其次是：没有存档的 JADE 对于相对低维的情况效果最好问题（D = 30），而带有存档的 JADE 在高维问题（D = 100）的情况下实现了最佳性能。可能是因为 400 的种群规模不足以解决各种 100 维问题，而存档可以通过在变异操作中引入更多的多样性来在一定程度上缓解这个问题。在这两种情况下（有或没有存档），JADE 对于 f1-f7 和 f10-f13 的优化收敛速度最快，这些优化可以是单峰或多峰、干净的或嘈杂的、连续的或不连续的。在f8和f9的情况下，jDE表现最好，JADE取得了非常有竞争力的结果。
SaDE和PSO的收敛速度通常比JADE和jDE差，但比DE/rand/1/bin好。

其次，比较不同算法的可靠性很重要，如表六和表七所示。 PSO 和 DE/rand/1/bin 表现最差，因为前者经常遭受过早收敛，而后者通常在有限数量的函数评估内收敛得非常慢。 SaDE 优于 PSO 和 DE/rand/1/bin，但对于某些问题显然不太令人满意，尤其是当问题维度较高时。正如预期的那样，jDE 表现得非常好，因为它的底层变异策略“DE/rand/1”比贪婪策略更稳健。有趣的是，对于所有 13 个可扩展功能，JADE 的可靠性与 jDE 相似。 JADE的高可靠性和快速收敛源于自适应参数控制以及档案辅助“DE/current-to pbest/1”变异策略提供的方向信息和多样性改进。

对于低维 Dixon-Szegö 函数，表 VIII 中的仿真结果表明不存在明显优越的算法。这与文献[15]中的观察结果类似，对于这组函数，自适应算法相对于经典的 DE/rand/1/bin 并没有表现出明显的性能改进。经过进一步调查后，这一观察结果并不奇怪。首先，对 DE/rand/1/bin 进行各种模拟，其中 F 和 CR 从 {0.1, 0.3, 0.5, 0.7, 0.9} 中选择，表明 F = 0.5 和 CR = 0.9 的参数设置始终会导致最佳或接近的结果。所有 Dixon-Szegö 功能的最佳性能。其次，模拟结果还表明，在优化这些低维问题所需的少量代内，参数自适应无法有效发挥作用。

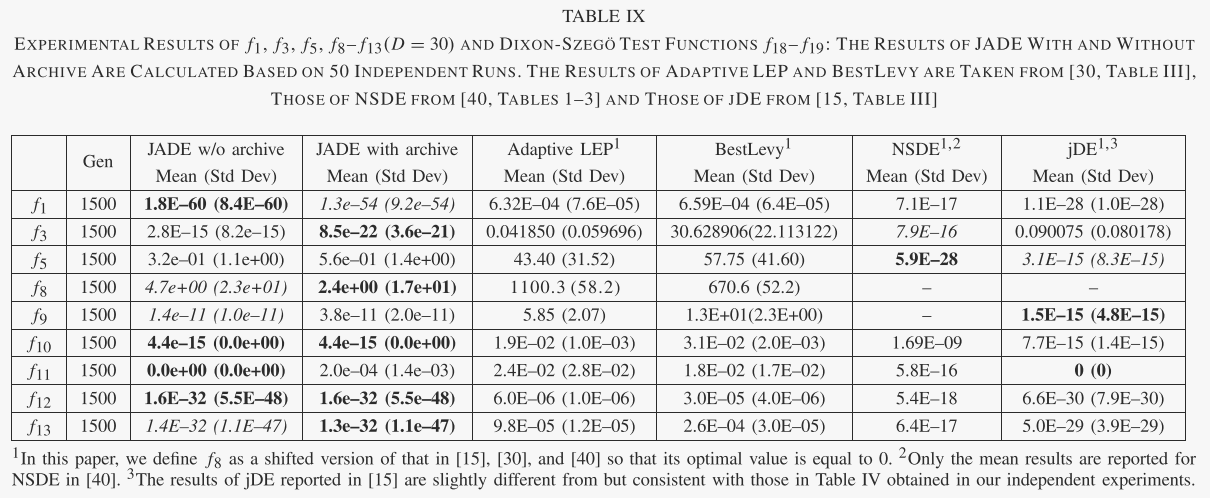
在表 IX 中，JADE 根据文献中报告的结果与其他进化算法进行了进一步比较：[30，表 III] 中的自适应 LEP 和 Best Levy 算法，[40，表 1-3] 中的 NSDE 和 [ 15，表三]。很明显，JADE 在大多数情况下表现最佳或次佳，并且总体性能优于其他竞争算法。

B. The Benefit of JADE Components

我们有兴趣确定没有存档的 JADE 的两个组件的好处：“DE/当前到 pbest”突变策略和参数适应。为此，我们考虑 JADE 的两种变体，即 rand-JADE 和 nonaJADE。它们与无存档的 JADE 的不同之处仅在于 rand-JADE 实现了 DE/rand/1（而不是 DE/current-to-pbest）突变策略，而 nona-JADE 没有采用自适应参数控制[即，而不是根据更新 μCR 和 μF对于（9）和（11），我们在整个优化过程中设置μCR = μF = 0.5（8）和（10）]。

表VI和表VII总结了JADE、rand-JADE、nona-JADE和DE/rand/1/bin的模拟结果。 FESS 性能表明，nona-JADE（在大多数情况下）和 rand-JADE（在某些情况下）收敛速度比 DE/rand/1/bin 更快，这分别是由于它们相对贪婪的突变策略和自适应参数控制。然而，rand-JADE 和 nona-JADE 都经常遭受某些函数的过早收敛问题。比如rand-JADE在f3和f5的优化上，成功率显然不太理想。这意味着由于 f3 和 f5 的病态 Hessian 矩阵（指示窄谷）围绕最优点，rand-JADE 无法维持足够高的种群多样性。

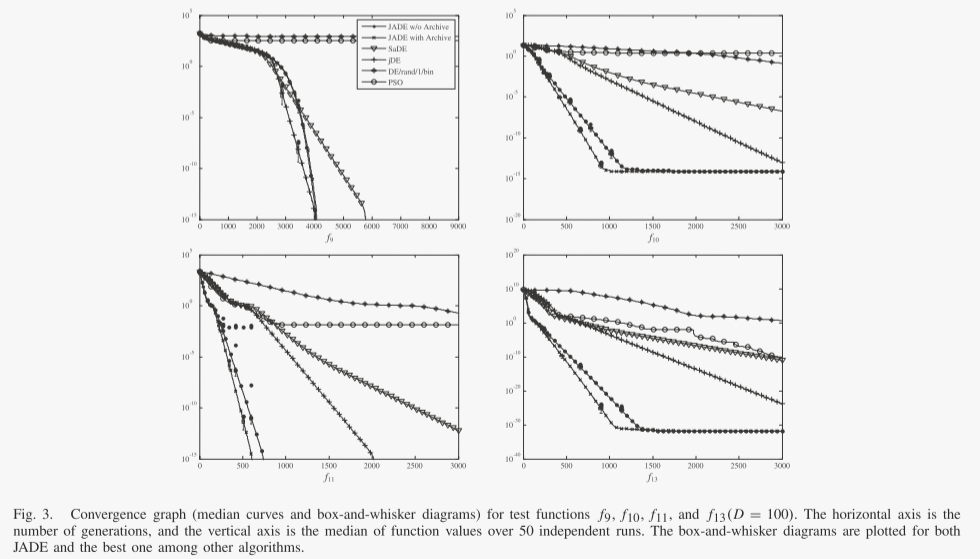
与它的两个变体相比，JADE 在收敛速度和可靠性方面取得了明显更好的性能。它表明贪心策略“DE/current-to- pbest”与参数自适应之间的互利合作。事实上，贪婪突变策略可能会在两个相反的方向上影响种群多样性：它倾向于通过使个体更接近一些最佳解决方案来降低多样性，但也有可能通过加快进程中的优化搜索来增加多样性方向。在没有参数自适应的经典DE算法中，贪婪变异策略通常会导致过早收敛，因为前者的多样性降低效应起着关键作用。然而，参数自适应方案能够将参数自适应为合适的值，从而提高“DE/current-to-pbest”在有希望的方向上的进度。这样，多样性增加的后一种效果就能够平衡前一种效果，提高了算法的收敛性能。

C. Evolution of μF and μCR in JADE

在经典DE中，两个控制参数F和CR需要针对不同的优化函数通过反复试验来调整。

在 JADE 中，它们由自适应参数 μF 和 μCR 控制，这些参数随着算法的进行而变化。 μF 和 μCR 的演变如图 4 所示，其中包含平均曲线和误差线。误差线表明 μF 和 μCR 在 50 次独立运行中的明显演变趋势。例如，在球函数f1的优化中，μF和μCR变化很小。这是合理的，因为在不同的演化阶段，景观的形状是相同的。对于椭球函数f3，μF和μCR在经历明显的初始变化后进入稳定状态（即最初分布在正方形区域的种群逐渐适应椭球景观）。与f5的情况类似，当种群落入Rosenbrock函数的窄谷后，μF和μCR达到稳态。对于 f9，随着算法的进行，景观显示出不同的形状，因此 μF 和 μCR 相应地演化为不同的值。

这些观察结果与直觉一致；即，对于各种问题（甚至对于球函数f1和椭球函数f3等可线性变换的问题）或单个问题的不同演化阶段（例如f9），F或CR没有固定的参数设置。

我们进一步研究了μF和μCR初始值对参数自适应过程的影响。根据大量的实验研究（限于篇幅，未报告结果），μF的初始值对算法的性能影响不大，而μCR的初始值建议中等至较大，特别是对于不可分离的函数。一般来说，初始设置 μCR = μF = 0.5 对于所有测试功能都适用，因此被认为是 JADE 的标准设置。

D. Parameter Values of JADE

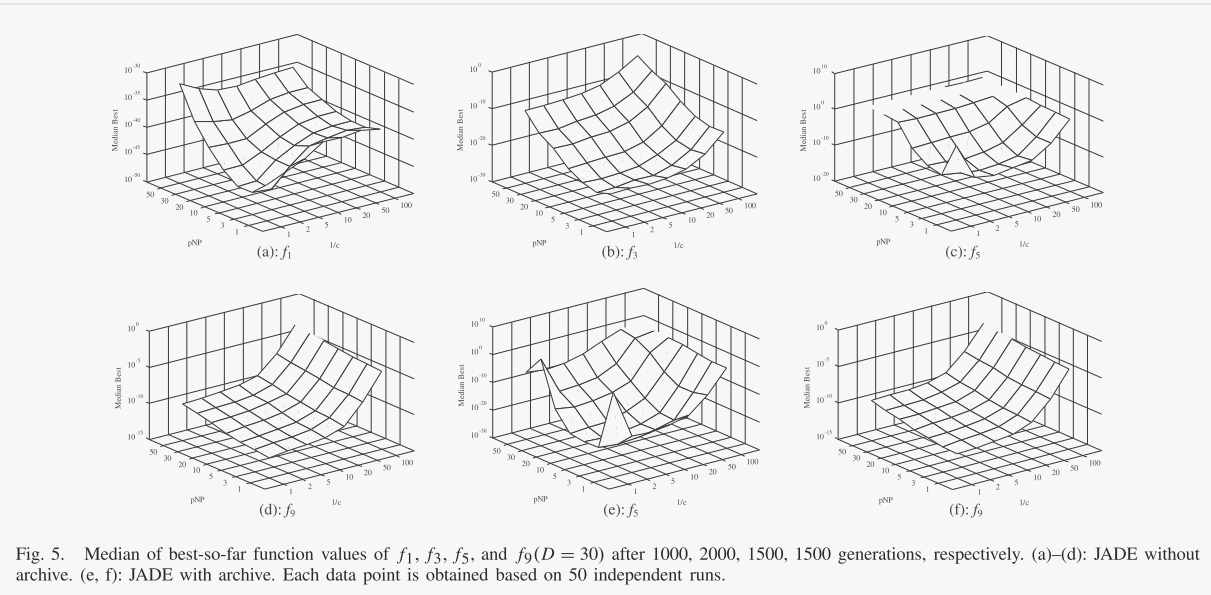
JADE引入了自己的参数c和p，分别决定μCR和μF的适应率以及突变策略的贪婪程度。根据它们在 JADE 中的作用，我们认为这两个参数对问题不敏感；因此，它比经典 DE 中与问题相关的参数选择（F 和 CR）更具优势。然而，找到适合不同问题的一系列参数仍然很有趣。如图 5 所示，绘制了具有不同参数组合的 JADE 的中值最佳值：1/c ∈ {1, 2, 5, 10, 20, 50, 100} 和 p · NP ∈{1, 3, 5 , 10, 20, 30, 50} 且 NP = 100。正如预期的那样，较小的值 1/c（例如 1/c = 1）或 p（例如 p · NP = 1）可能会导致不太令人满意的结果在某些情况下。前者由于缺乏足够的信息来平滑更新CR和F而导致错误收敛，而后者过于贪婪而无法维持种群的多样性。然而，很明显，JADE 在 c 和 p 的大范围内优于其他算法或具有竞争力（与图 2 和图 3 中其他算法的结果相比）。具体来说，它表明 JADE（有或没有存档）在值 1/c ∈ [5, 20] 和 p ∈ [5%, 20%] 时效果最佳。

VI. CONCLUSION

参数自适应通过在进化搜索过程中自动将控制参数更新为合适的值，有利于提高进化算法的优化性能。很自然地结合参数自适应和贪婪突变策略（例如“DE / current-to-pbest”）来提高收敛速度，同时保持算法的高可靠性。这促使我们考虑 JADE，一种参数自适应“当前到最佳”DE 算法。在“current-to-pbest”中，我们利用多个最佳解决方案的信息来平衡突变的贪婪性和种群的多样性。 JADE 的参数自适应是通过根据历史成功记录进化突变因子和交叉概率来实现的。我们还引入了一个外部档案来存储最近探索的较差解决方案，并将它们与当前群体的差异用作实现最优的有希望的方向。

JADE 已在一组取自文献的经典基准函数上进行了测试。与其他经典和自适应 DE 算法以及规范 PSO 算法相比，它在收敛速度和可靠性方面表现出更好或至少具有竞争力的优化性能。根据其报告的结果，JADE 还显示出优于文献中其他进化算法的优越性。

潜在研究点

JADE with archive 在优化高维问题方面显示出了可喜的结果。与协作协同进化[41]、[42]等其他技术相比，JADE 对于提高高维问题的收敛性能有着截然不同的侧重点。预计 JADE 可以作为一个适当的底层方案，其中结合了合作协同进化以实现更好的性能[43]，[44]。此外，将当前的工作扩展到 MOO 是很有趣的，因为参数自适应 MOO 被评论为“一个非常有趣的话题，很少有研究人员在专业文献中讨论过”[45]。虽然我们的初步研究已经显示出有希望的结果[46]，但将参数适应方案纳入多目标进化优化仍然存在许多悬而未决的问题。

文献链接