文章目录
- 前言
- 一、m 序列
- 1、m 序列的产生
- 2、m 序列的性质
- ①、均衡性
- ②、游程分布
- ③、移位相加特性
- ④、自相关函数
- ⑤、功率谱密度
- ⑥、伪噪声特性
- 二、M 序列
- 1、m 序列的产生
- 2、m 序列的性质
- 三、MATLAB 中 m 序列
- 1、m 序列生成函数的 MATLAB 代码
- 2、MATLAB 仿真
前言
在通信系统中的随机噪声会使模拟信号产生失真和使数字信号出现误码,并且,它还是限制信道容量的一个重要因素。因此人们经常希望消除或减小通信系统中的随机噪声。
另外,有时人们会希望获得随机噪声。例如,在实验室中对通信设备或系统性能进行测试时,可能要故意加人一定的随机噪声。
伪随机噪声具有类似于随机噪声的某些统计特性,同时又能够重复产生。由于它具有随机噪声的优点,又避免了随机噪声的缺点,因此获得了日益广泛的实际应用。目前广泛应用的伪随机噪声都是由周期性数字序列经过滤波等处理后得出的。在后面我们将这种周期性数字序列称为伪随机序列。它有时又称为伪随机信号和伪随机码。
一、m 序列
1、m 序列的产生
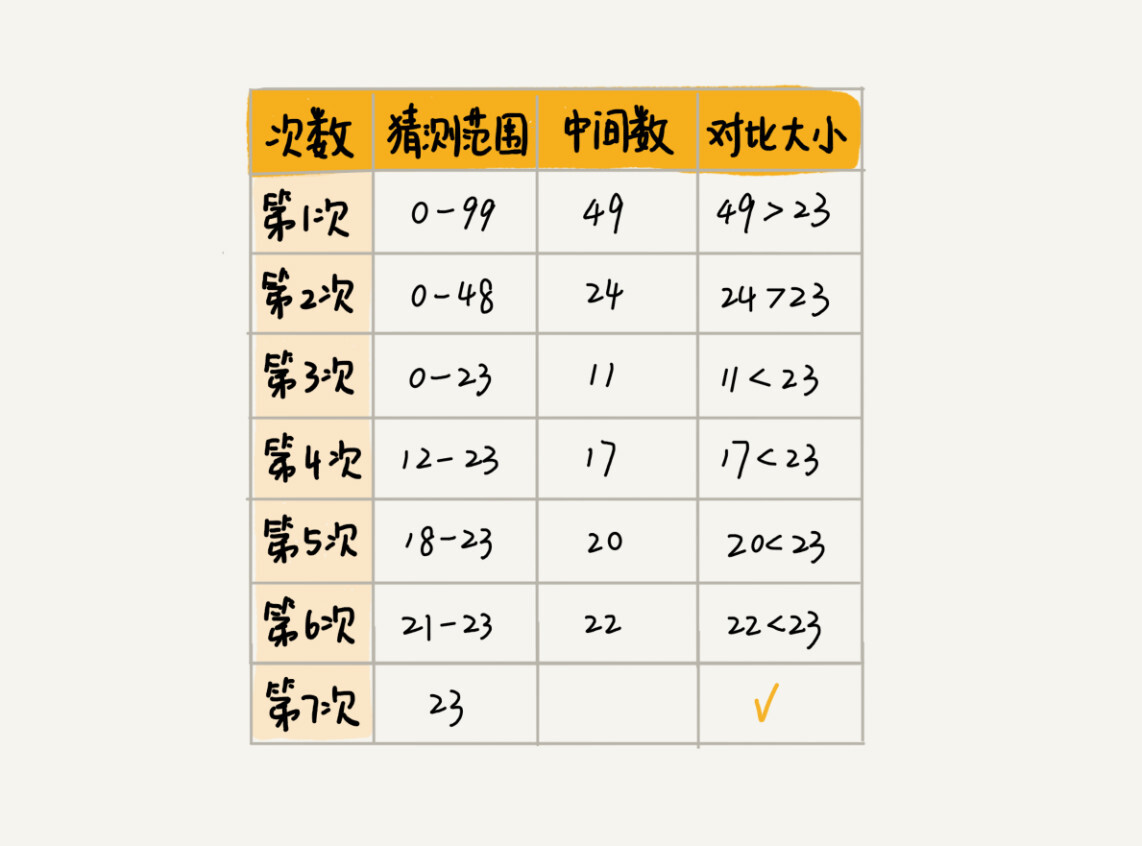
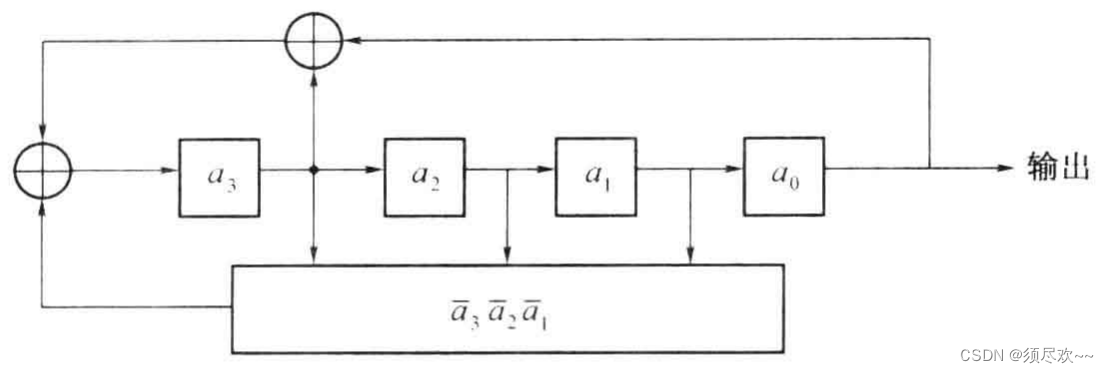
m 序列是最长线性反馈移位寄存器序列的简称。它是由带线性反馈的移存器产生的周期最长的序列。现在,我们先给出一个 m 序列的例子。在下图中示出一个 4 级线性反馈移存器。
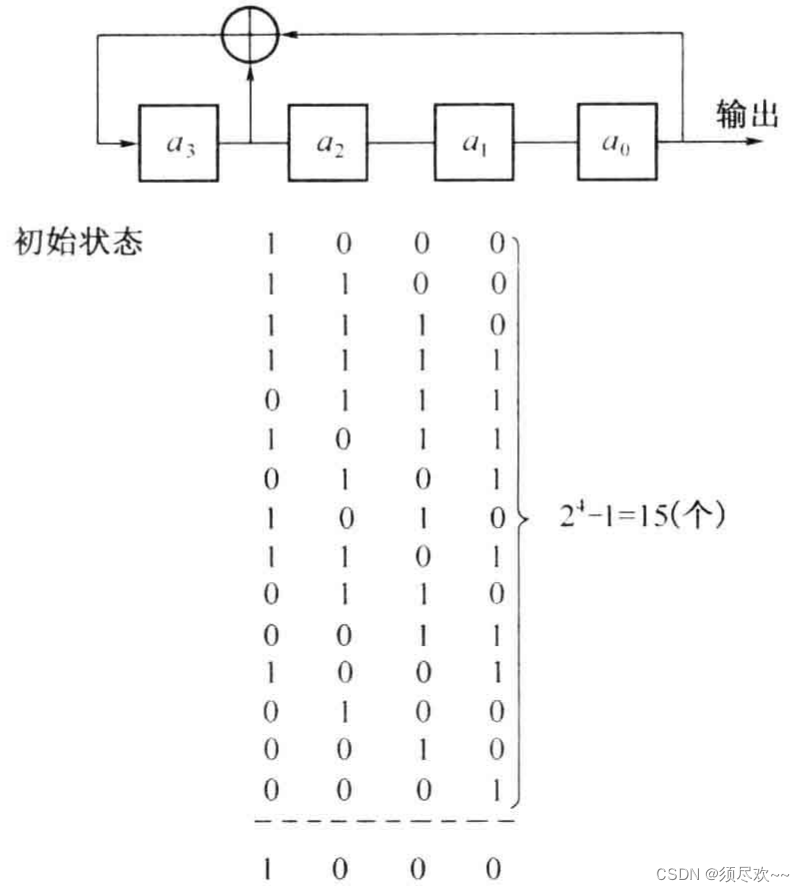
设其初始状态为 ( a 3 , a 2 , a 1 , a 0 ) = ( 1 , 0 , 0 , 0 ) (a_3,a_2,a_1,a_0)=(1,0,0,0) (a3,a2,a1,a0)=(1,0,0,0),则在移位一次时,由 a 3 a_3 a3 和 a 2 a_2 a2 模 2 相加产生新的输入 a 4 = 1 ⊕ 0 = 1 a_4=1\oplus0=1 a4=1⊕0=1,新的状态变为 ( a 4 , a 3 , a 2 , a 1 ) = ( 1 , 1 , 0 , 0 ) (a_4,a_3,a_2,a_1)=(1,1,0,0) (a4,a3,a2,a1)=(1,1,0,0)。这样移位15 次后又回到初始状态 ( 1 , 0 , 0 , 0 ) (1,0,0,0) (1,0,0,0)。不难看出若初始状态为全 “0” 即 (0,0,0,0) 则移位后得到的仍为全 “0” 状态。这就意味着在这种反馈移存器中应该避免出现全 “0” 状态,否则移存器的状态将不会改变。因为 4 级移存器共有 2 4 = 16 2^4=16 24=16 种可能的状态。除全 “0” 状态外,只剩 15 种状态可用。这就是说,由任何 4 级反馈移存器产生的序列的周期最长为15.
我们常常希望用尽可能少的级数产生尽可能长的序列。由上例可见,一般来说,一个 n 级线性反馈移存器可能产生的最长周期等于
(
2
n
−
1
)
(2^n-1)
(2n−1)。我们将这种最长的序列称为最长线性反馈移存器序列(maximal length linear feedback shift register sequence),简称 m 序列。
2、m 序列的性质
①、均衡性
在 m 序列的一个周期中,“1” 和 “0” 的数目基本相等。准确地说,“1” 的个数比 “0” 的个数多一个。
②、游程分布
我们把一个序列中取值相同的那些相继的(连在一起的)元素合称为一个 “游程(run)”。在一个游程中元素的个数称为游程长度。例如,在上图中给出的 m 序列可以重写为:
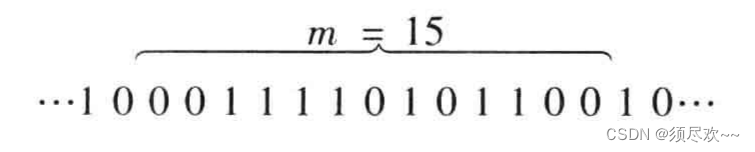
在其一个周期(m 个元素)中,共有 8 个游程,其中长度为 4 的游程有一个,即 “1 1 1 1”,长度为 3 的游程有一个,即 “0 0 0”,长度为 2 的游程有两个,即 “1 1” 和 “0 0”,长度为 1 的游程有 4 个即两个 “1” 和两个 “0”
一般说来,在 m 序列中,长度为 1 的游程占游程总数的 1/2;长度为 2 的游程占游程总数的 1/4;长度为 3 的游程占1/8。严格讲,长度为 k k k 的游程数目占游程总数的 2 − k 2^{-k} 2−k,其中 1 ≤ k ≤ ( n − 1 ) 1\le k\le (n-1) 1≤k≤(n−1)。而且在长度为 k k k 的游程中(其中 1 ≤ k ≤ ( n − 2 ) 1\le k\le (n-2) 1≤k≤(n−2))。连 “1” 的游程和连 “0” 的游程各占一半。
③、移位相加特性
一个
m
m
m 序列
M
p
M_p
Mp 与其经过任意次延迟移位产生的另一个不同序列
M
r
M_r
Mr 模 2 相加得到的仍是
M
p
M_p
Mp 的某次延迟移位序列
M
s
M_s
Ms 即:
M
p
⊕
M
r
=
M
s
M_p \oplus M_r=M_s
Mp⊕Mr=Ms
④、自相关函数
下图为 m 序列的自相关函数。图中的圆点表示
j
j
j 取整数时的
ρ
(
j
)
\rho(j)
ρ(j) 取值,而折线是
R
(
τ
)
R(\tau)
R(τ) 的连续曲线。可以看出,两者是重合的。由图还可以看出当周期
T
0
T_0
T0 非常长和码元宽度
T
0
/
m
T_0/m
T0/m 极小时
R
(
τ
)
R(\tau)
R(τ) 近似于冲激函数
δ
(
t
)
\delta(t)
δ(t) 的形状。
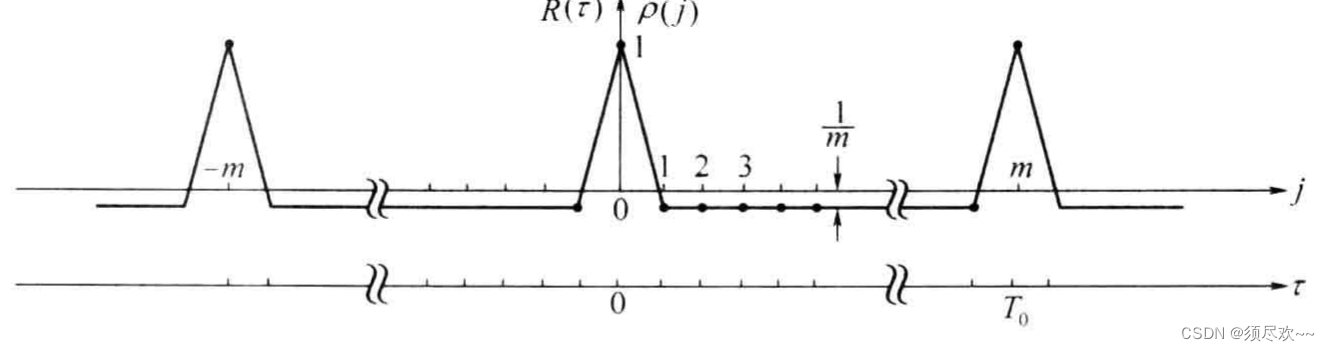
由上述可知,m 序列的自相关函数只有两种取值:0 和 (1/m)。有时我们把这类自相关函数只有两种取值的序列称为双值自相关序列。
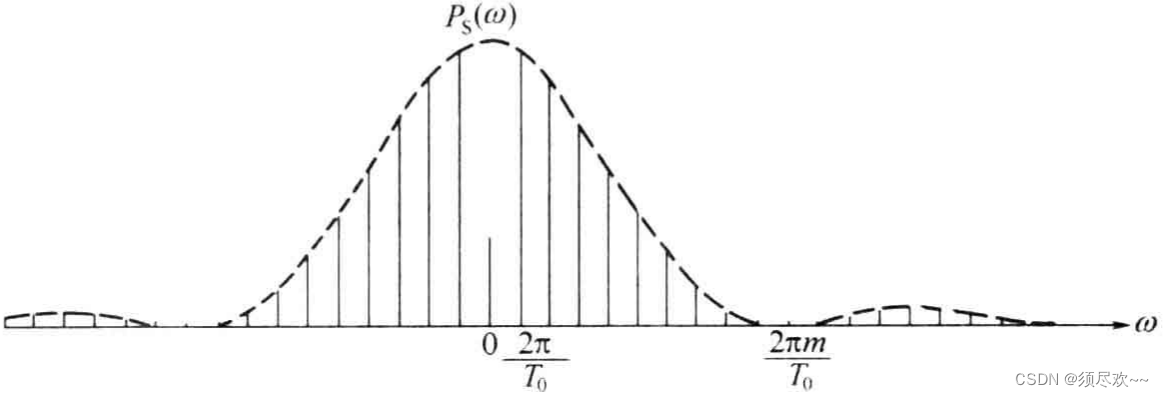
⑤、功率谱密度
对 m 序列的自相关函数做傅里叶变换可以得到其功率谱密度。
⑥、伪噪声特性
由于 m 序列的均衡性、游程分布和自相关特性与随机序列的基本性质极相似所以通常将 m 序列称为伪噪声(PN)序列,或称为伪随机序列。
二、M 序列
由非线性反馈移存器产生的周期最长的序列称为 M 序列。它和上述 m 序列不同,后者是由线性反馈移存器产生的周期最长的序列。
由 m 序列产生器的分析可知,一个 n 级 m 序列产生器只可能有
(
2
n
−
1
)
(2^n-1)
(2n−1) 种不同的状态。但是 n 级移存器最多可有
2
n
2^n
2n 种状态,在 m 序列中不能出现的是全 “0” 状态。在线性反馈条件下,全 “0” 状态出现后,产生器的状态将不会再改变;但是在非线性反馈条件下,却不一定如此。因此,非线性反馈移存器的最长周期可达
2
n
2^n
2n,我们称这种周期长达
2
n
2^n
2n 的序列为 M 序列。
1、m 序列的产生
参考上面 m 序列的产生 图,它是一个 n=4 级的 m 序列产生器。图中给出了它的 15 种状态。若使它增加一个 “000”状态,就可变成 M 序列产生器了。因为移存器中后级状态必须是由其前级状态移入而得,故此 “0000” 状态必须处于初始状态 “1000” 之前和 “0001” 状态之后。这就是说,我们需要将其递推方程修改为非线性方程,使 “0001” 状态代入新的递推方程后,产生状态 “0000”(而不是“1000”),并且在 “0000” 状态代入后产生状态 “1000”(而不是保持“0000”不变)。
2、m 序列的性质
M 序列与 m 序列类似,也在一定程度上具有噪声特性。它满足 m 序列的前两个:
- 在 M 序列的一个周期中,出现 “0” 与 “1” 的数目相等
- 在 n 级 M 序列的一个周期中,游程共有 2 n − 1 2^{n-1} 2n−1 个,其中长度为 k k k 的游程占 1 / 2 k 1/2^k 1/2k, 1 < k ≤ n − 2 1<k≤n-2 1<k≤n−2;长为 n n n 的游程有两个,没有长为 ( n − 1 ) (n-1) (n−1) 的游程。在同长的游程中,“0” 游程和 “1” 游程各占 1/2。
M 序列与 m 序列相比,最主要的优点是数量大,即同样级数 n 的移存器能够产生的平移不等价 M 序列总数比 m 序列的大得多,且随 n 的增大迅速增加。在下表中给出了级数 n 与可能产生的两种序列数目的比较。

三、MATLAB 中 m 序列
1、m 序列生成函数的 MATLAB 代码
mseq.m
function [mout] = mseq(n, taps, inidata, num)
% ****************************************************************
% n : m序列的阶数n
% taps : 反馈寄存器的连接位置
% inidata : 寄存器的初始值序列
% num : 输出的m序列的个数
% mout : 输出的m序列,如果num>1,则每一行为一个m序列
% ****************************************************************
mout = zeros(num,2^n-1);
fpos = zeros(n,1);
fpos(taps) = 1;
for ii=1:2^n-1
mout(1,ii) = inidata(n); % 寄存器的输出值
temp = mod(inidata*fpos,2); % 计算反馈数据
inidata(2:n) = inidata(1:n-1); % 寄存器移位一次
inidata(1) = temp; % 更新第1个寄存器的值
end
if num > 1 %如果要输出多个m序列,生成其他m序列
for ii=2:num
mout(ii,:) = shift(mout(ii-1,:),1);
end
end
2、MATLAB 仿真
function code = mseq(n, taps, init, len)
code = mseq(3,[1 3],[1 1 1],52);
disp(code);
- 参数 n 代表 m 序列的阶数,即序列的长度为 2 n − 1 2^n-1 2n−1。输入参数 n 必须是一个正整数。
- 参数 taps 是一个一维向量,指定用于生成 m 序列的反馈多项式的系数。这些系数表示了多项式中的项是否参与反馈。例如,如果taps为[1 3],则反馈多项式为 1 + z 3 1 + z^3 1+z3,其中 z 表示序列的延迟操作。
- 参数 init 是一个一维向量,指定 m 序列的初始状态。该向量的长度必须小于或等于 n。如果 init 的长度小于n,则在其前面填充零。
- 参数 len 表示要生成的 m 序列的长度。
可以看到如下结果:
生成的 code 是一个 52 × 7 double 类型:
1 1 1 0 1 0 0
0 1 1 1 0 1 0
0 0 1 1 1 0 1
1 0 0 1 1 1 0
0 1 0 0 1 1 1
1 0 1 0 0 1 1
1 1 0 1 0 0 1
1 1 1 0 1 0 0
0 1 1 1 0 1 0
0 0 1 1 1 0 1
1 0 0 1 1 1 0
0 1 0 0 1 1 1
1 0 1 0 0 1 1
1 1 0 1 0 0 1
1 1 1 0 1 0 0
0 1 1 1 0 1 0
0 0 1 1 1 0 1
1 0 0 1 1 1 0
0 1 0 0 1 1 1
1 0 1 0 0 1 1
1 1 0 1 0 0 1
1 1 1 0 1 0 0
0 1 1 1 0 1 0
0 0 1 1 1 0 1
1 0 0 1 1 1 0
0 1 0 0 1 1 1
1 0 1 0 0 1 1
1 1 0 1 0 0 1
1 1 1 0 1 0 0
0 1 1 1 0 1 0
0 0 1 1 1 0 1
1 0 0 1 1 1 0
0 1 0 0 1 1 1
1 0 1 0 0 1 1
1 1 0 1 0 0 1
1 1 1 0 1 0 0
0 1 1 1 0 1 0
0 0 1 1 1 0 1
1 0 0 1 1 1 0
0 1 0 0 1 1 1
1 0 1 0 0 1 1
1 1 0 1 0 0 1
1 1 1 0 1 0 0
0 1 1 1 0 1 0
0 0 1 1 1 0 1
1 0 0 1 1 1 0
0 1 0 0 1 1 1
1 0 1 0 0 1 1
1 1 0 1 0 0 1
1 1 1 0 1 0 0
0 1 1 1 0 1 0
0 0 1 1 1 0 1
我的qq:2442391036,欢迎交流!